Deep Sketched Output Kernel Regression for Structured Prediction

By leveraging the kernel trick in the output space, kernel-induced losses provide a principled way to define structured output prediction tasks for a wide variety of output modalities. In particular, they have been successfully used in the context of surrogate non-parametric regression, where the kernel trick is typically exploited in the input space as well. However, when inputs are images or texts, more expressive models such as deep neural networks seem more suited than non-parametric methods. In this work, we tackle the question of how to train neural networks to solve structured output prediction tasks, while still benefiting from the versatility and relevance of kernel-induced losses. We design a novel family of deep neural architectures, whose last layer predicts in a data-dependent finite-dimensional subspace of the infinite-dimensional output feature space deriving from the kernel-induced loss. This subspace is chosen as the span of the eigenfunctions of a randomly-approximated version of the empirical kernel covariance operator. Interestingly, this approach unlocks the use of gradient descent algorithms (and consequently of any neural architecture) for structured prediction. Experiments on synthetic tasks as well as real-world supervised graph prediction problems show the relevance of our method.

Multitask Online Learning: Listen to the Neighborhood Buzz

We study multitask online learning in a setting where agents can only exchange information with their neighbors on an arbitrary communication network. We introduce $\texttt{MT-CO}_2\texttt{OL}$, a decentralized algorithm for this setting whose regret depends on the interplay between the task similarities and the network structure. Our analysis shows that the regret of $\texttt{MT-CO}_2\texttt{OL}$ is never worse (up to constants) than the bound obtained when agents do not share information. On the other hand, our bounds significantly improve when neighboring agents operate on similar tasks. In addition, we prove that our algorithm can be made differentially private with a negligible impact on the regret when the losses are linear. Finally, we provide experimental support for our theory.

Multitask Learning with No Regret: from Improved Confidence Bounds to Active Learning

Multitask learning is a powerful framework that enables one to simultaneously learn multiple related tasks by sharing information between them. Quantifying uncertainty in the estimated tasks is of pivotal importance for many downstream applications, such as online or active learning. In this work, we provide novel multitask confidence intervals in the challenging agnostic setting, i.e., when neither the similarity between tasks nor the tasks' features are available to the learner. The obtained intervals do not require i.i.d. data and can be directly applied to bound the regret in online learning. Through a refined analysis of the multitask information gain, we obtain new regret guarantees that, depending on a task similarity parameter, can significantly improve over treating tasks independently. We further propose a novel online learning algorithm that achieves such improved regret without knowing this parameter in advance, i.e., automatically adapting to task similarity. As a second key application of our results, we introduce a novel multitask active learning setup where several tasks must be simultaneously optimized, but only one of them can be queried for feedback by the learner at each round. For this problem, we design a no-regret algorithm that uses our confidence intervals to decide which task should be queried. Finally, we empirically validate our bounds and algorithms on synthetic and real-world (drug discovery) data.

Sketch In, Sketch Out: Accelerating both Learning and Inference for Structured Prediction with Kernels

Surrogate kernel-based methods offer a flexible solution to structured output prediction by leveraging the kernel trick in both input and output spaces. In contrast to energy-based models, they avoid to pay the cost of inference during training, while enjoying statistical guarantees. However, without approximation, these approaches are condemned to be used only on a limited amount of training data. In this paper, we propose to equip surrogate kernel methods with approximations based on sketching, seen as low rank projections of feature maps both on input and output feature maps. We showcase the approach on Input Output Kernel ridge Regression (or Kernel Dependency Estimation) and provide excess risk bounds that can be in turn directly plugged on the final predictive model. An analysis of the complexity in time and memory show that sketching the input kernel mostly reduces training time while sketching the output kernel allows to reduce the inference time. Furthermore, we show that Gaussian and sub-Gaussian sketches are admissible sketches in the sense that they induce projection operators ensuring a small excess risk. Experiments on different tasks consolidate our findings.

Linear Bandits with Memory: from Rotting to Rising

Nonstationary phenomena, such as satiation effects in recommendation, are a common feature of sequential decision-making problems. While these phenomena have been mostly studied in the framework of bandits with finitely many arms, in many practically relevant cases linear bandits provide a more effective modeling choice. In this work, we introduce a general framework for the study of nonstationary linear bandits, where current rewards are influenced by the learner's past actions in a fixed-size window. In particular, our model includes stationary linear bandits as a special case. After showing that the best sequence of actions is NP-hard to compute in our model, we focus on cyclic policies and prove a regret bound for a variant of the OFUL algorithm that balances approximation and estimation errors. Our theoretical findings are supported by experiments (which also include misspecified settings) where our algorithm is seen to perform well against natural baselines.

On Medians of (Randomized) Pairwise Means

Tournament procedures, recently introduced in Lugosi & Mendelson (2016), offer an appealing alternative, from a theoretical perspective at least, to the principle of Empirical Risk Minimization in machine learning. Statistical learning by Median-of-Means (MoM) basically consists in segmenting the training data into blocks of equal size and comparing the statistical performance of every pair of candidate decision rules on each data block: that with highest performance on the majority of the blocks is declared as the winner. In the context of nonparametric regression, functions having won all their duels have been shown to outperform empirical risk minimizers w.r.t. the mean squared error under minimal assumptions, while exhibiting robustness properties. It is the purpose of this paper to extend this approach in order to address other learning problems, in particular for which the performance criterion takes the form of an expectation over pairs of observations rather than over one single observation, as may be the case in pairwise ranking, clustering or metric learning. Precisely, it is proved here that the bounds achieved by MoM are essentially conserved when the blocks are built by means of independent sampling without replacement schemes instead of a simple segmentation. These results are next extended to situations where the risk is related to a pairwise loss function and its empirical counterpart is of the form of a $U$-statistic. Beyond theoretical results guaranteeing the performance of the learning/estimation methods proposed, some numerical experiments provide empirical evidence of their relevance in practice.

$p$-Sparsified Sketches for Fast Multiple Output Kernel Methods

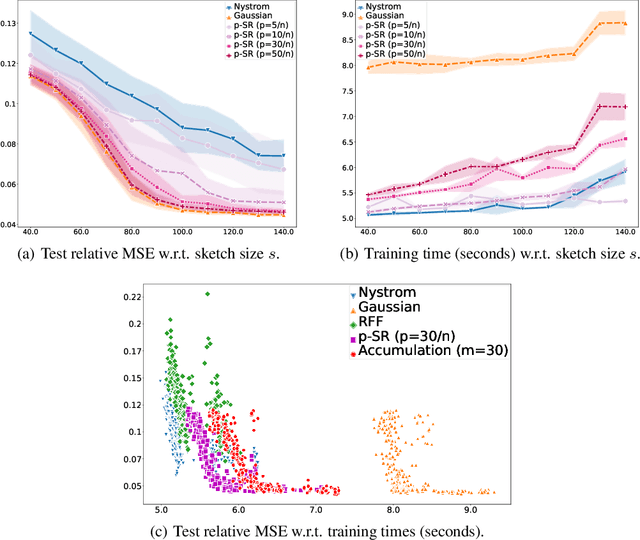
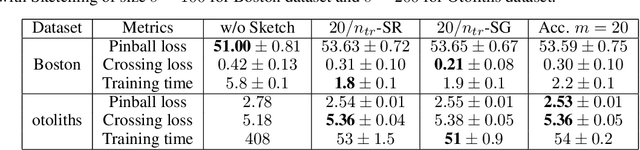
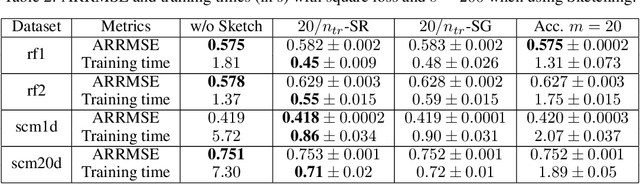
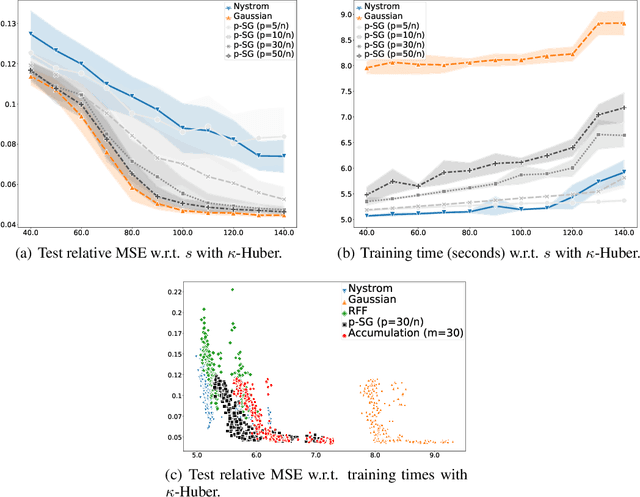
Kernel methods are learning algorithms that enjoy solid theoretical foundations while suffering from important computational limitations. Sketching, that consists in looking for solutions among a subspace of reduced dimension, is a widely studied approach to alleviate this numerical burden. However, fast sketching strategies, such as non-adaptive subsampling, significantly degrade the guarantees of the algorithms, while theoretically-accurate sketches, such as the Gaussian one, turn out to remain relatively slow in practice. In this paper, we introduce the $p$-sparsified sketches, that combine the benefits from both approaches to achieve a good tradeoff between statistical accuracy and computational efficiency. To support our method, we derive excess risk bounds for both single and multiple output problems, with generic Lipschitz losses, providing new guarantees for a wide range of applications, from robust regression to multiple quantile regression. We also provide empirical evidences of the superiority of our sketches over recent SOTA approaches.

AdaTask: Adaptive Multitask Online Learning

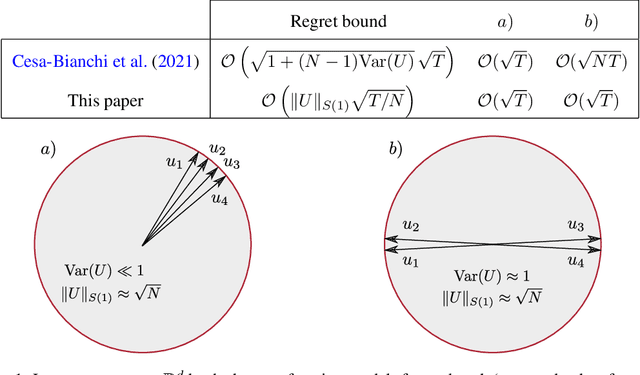
We introduce and analyze AdaTask, a multitask online learning algorithm that adapts to the unknown structure of the tasks. When the $N$ tasks are stochastically activated, we show that the regret of AdaTask is better, by a factor that can be as large as $\sqrt{N}$, than the regret achieved by running $N$ independent algorithms, one for each task. AdaTask can be seen as a comparator-adaptive version of Follow-the-Regularized-Leader with a Mahalanobis norm potential. Through a variational formulation of this potential, our analysis reveals how AdaTask jointly learns the tasks and their structure. Experiments supporting our findings are presented.

Break your Bandit Routine with LSD Rewards: a Last Switch Dependent Analysis of Satiation and Seasonality

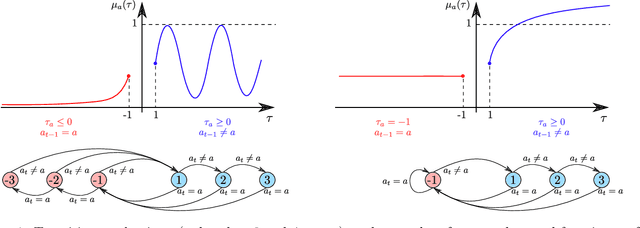
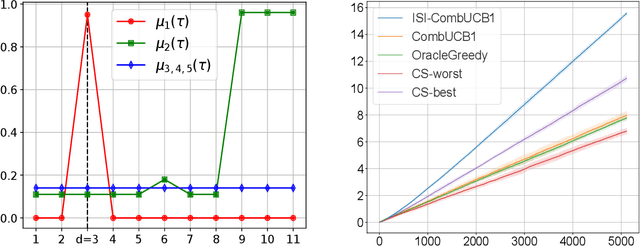
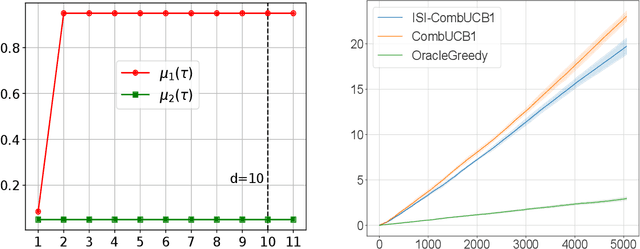
Motivated by the fact that humans like some level of unpredictability or novelty, and might therefore get quickly bored when interacting with a stationary policy, we introduce a novel non-stationary bandit problem, where the expected reward of an arm is fully determined by the time elapsed since the arm last took part in a switch of actions. Our model generalizes previous notions of delay-dependent rewards, and also relaxes most assumptions on the reward function. This enables the modeling of phenomena such as progressive satiation and periodic behaviours. Building upon the Combinatorial Semi-Bandits (CSB) framework, we design an algorithm and prove a bound on its regret with respect to the optimal non-stationary policy (which is NP-hard to compute). Similarly to previous works, our regret analysis is based on defining and solving an appropriate trade-off between approximation and estimation. Preliminary experiments confirm the superiority of our algorithm over both the oracle greedy approach and a vanilla CSB solver.

Visual Recognition with Deep Learning from Biased Image Datasets

In practice, and more especially when training deep neural networks, visual recognition rules are often learned based on various sources of information. On the other hand, the recent deployment of facial recognition systems with uneven predictive performances on different population segments highlights the representativeness issues possibly induced by a naive aggregation of image datasets. Indeed, sampling bias does not vanish simply by considering larger datasets, and ignoring its impact may completely jeopardize the generalization capacity of the learned prediction rules. In this paper, we show how biasing models, originally introduced for nonparametric estimation in (Gill et al., 1988), and recently revisited from the perspective of statistical learning theory in (Laforgue and Cl\'emen\c{c}on, 2019), can be applied to remedy these problems in the context of visual recognition. Based on the (approximate) knowledge of the biasing mechanisms at work, our approach consists in reweighting the observations, so as to form a nearly debiased estimator of the target distribution. One key condition for our method to be theoretically valid is that the supports of the distributions generating the biased datasets at disposal must overlap, and cover the support of the target distribution. In order to meet this requirement in practice, we propose to use a low dimensional image representation, shared across the image databases. Finally, we provide numerical experiments highlighting the relevance of our approach whenever the biasing functions are appropriately chosen.