Deep Sketched Output Kernel Regression for Structured Prediction

By leveraging the kernel trick in the output space, kernel-induced losses provide a principled way to define structured output prediction tasks for a wide variety of output modalities. In particular, they have been successfully used in the context of surrogate non-parametric regression, where the kernel trick is typically exploited in the input space as well. However, when inputs are images or texts, more expressive models such as deep neural networks seem more suited than non-parametric methods. In this work, we tackle the question of how to train neural networks to solve structured output prediction tasks, while still benefiting from the versatility and relevance of kernel-induced losses. We design a novel family of deep neural architectures, whose last layer predicts in a data-dependent finite-dimensional subspace of the infinite-dimensional output feature space deriving from the kernel-induced loss. This subspace is chosen as the span of the eigenfunctions of a randomly-approximated version of the empirical kernel covariance operator. Interestingly, this approach unlocks the use of gradient descent algorithms (and consequently of any neural architecture) for structured prediction. Experiments on synthetic tasks as well as real-world supervised graph prediction problems show the relevance of our method.

Sketch In, Sketch Out: Accelerating both Learning and Inference for Structured Prediction with Kernels

Surrogate kernel-based methods offer a flexible solution to structured output prediction by leveraging the kernel trick in both input and output spaces. In contrast to energy-based models, they avoid to pay the cost of inference during training, while enjoying statistical guarantees. However, without approximation, these approaches are condemned to be used only on a limited amount of training data. In this paper, we propose to equip surrogate kernel methods with approximations based on sketching, seen as low rank projections of feature maps both on input and output feature maps. We showcase the approach on Input Output Kernel ridge Regression (or Kernel Dependency Estimation) and provide excess risk bounds that can be in turn directly plugged on the final predictive model. An analysis of the complexity in time and memory show that sketching the input kernel mostly reduces training time while sketching the output kernel allows to reduce the inference time. Furthermore, we show that Gaussian and sub-Gaussian sketches are admissible sketches in the sense that they induce projection operators ensuring a small excess risk. Experiments on different tasks consolidate our findings.

$p$-Sparsified Sketches for Fast Multiple Output Kernel Methods

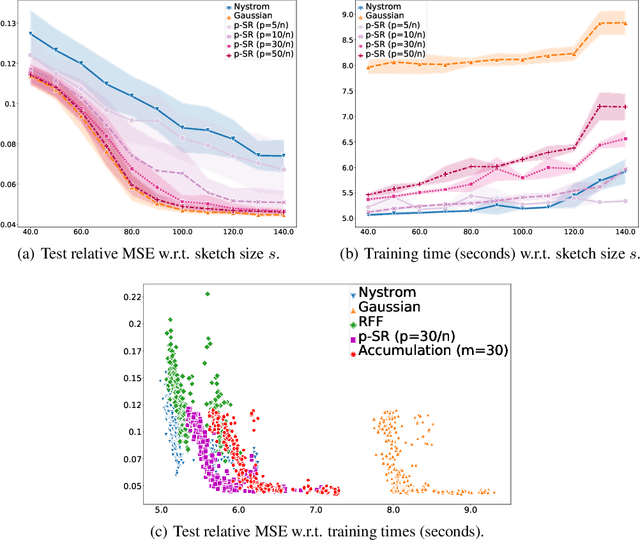
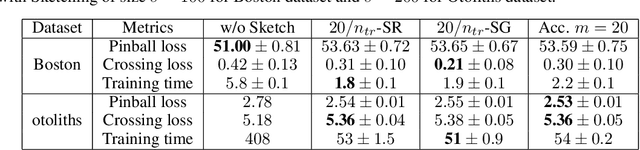
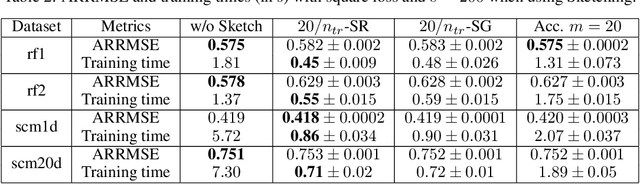
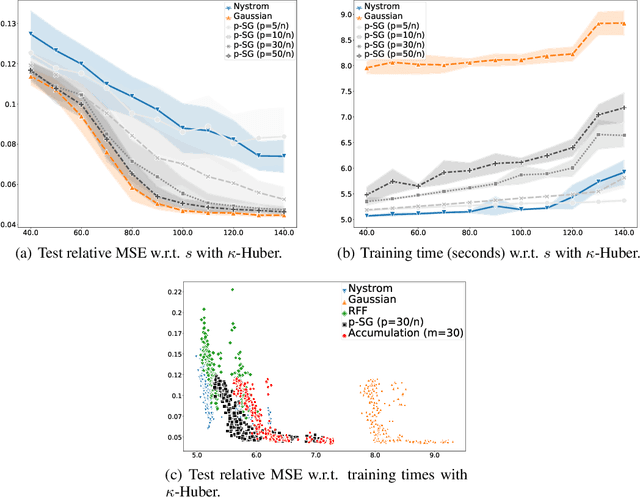
Kernel methods are learning algorithms that enjoy solid theoretical foundations while suffering from important computational limitations. Sketching, that consists in looking for solutions among a subspace of reduced dimension, is a widely studied approach to alleviate this numerical burden. However, fast sketching strategies, such as non-adaptive subsampling, significantly degrade the guarantees of the algorithms, while theoretically-accurate sketches, such as the Gaussian one, turn out to remain relatively slow in practice. In this paper, we introduce the $p$-sparsified sketches, that combine the benefits from both approaches to achieve a good tradeoff between statistical accuracy and computational efficiency. To support our method, we derive excess risk bounds for both single and multiple output problems, with generic Lipschitz losses, providing new guarantees for a wide range of applications, from robust regression to multiple quantile regression. We also provide empirical evidences of the superiority of our sketches over recent SOTA approaches.