Learning Controlled Stochastic Differential Equations

Identification of nonlinear dynamical systems is crucial across various fields, facilitating tasks such as control, prediction, optimization, and fault detection. Many applications require methods capable of handling complex systems while providing strong learning guarantees for safe and reliable performance. However, existing approaches often focus on simplified scenarios, such as deterministic models, known diffusion, discrete systems, one-dimensional dynamics, or systems constrained by strong structural assumptions such as linearity. This work proposes a novel method for estimating both drift and diffusion coefficients of continuous, multidimensional, nonlinear controlled stochastic differential equations with non-uniform diffusion. We assume regularity of the coefficients within a Sobolev space, allowing for broad applicability to various dynamical systems in robotics, finance, climate modeling, and biology. Leveraging the Fokker-Planck equation, we split the estimation into two tasks: (a) estimating system dynamics for a finite set of controls, and (b) estimating coefficients that govern those dynamics. We provide strong theoretical guarantees, including finite-sample bounds for \(L^2\), \(L^\infty\), and risk metrics, with learning rates adaptive to coefficients' regularity, similar to those in nonparametric least-squares regression literature. The practical effectiveness of our approach is demonstrated through extensive numerical experiments. Our method is available as an open-source Python library.

Sketch In, Sketch Out: Accelerating both Learning and Inference for Structured Prediction with Kernels

Surrogate kernel-based methods offer a flexible solution to structured output prediction by leveraging the kernel trick in both input and output spaces. In contrast to energy-based models, they avoid to pay the cost of inference during training, while enjoying statistical guarantees. However, without approximation, these approaches are condemned to be used only on a limited amount of training data. In this paper, we propose to equip surrogate kernel methods with approximations based on sketching, seen as low rank projections of feature maps both on input and output feature maps. We showcase the approach on Input Output Kernel ridge Regression (or Kernel Dependency Estimation) and provide excess risk bounds that can be in turn directly plugged on the final predictive model. An analysis of the complexity in time and memory show that sketching the input kernel mostly reduces training time while sketching the output kernel allows to reduce the inference time. Furthermore, we show that Gaussian and sub-Gaussian sketches are admissible sketches in the sense that they induce projection operators ensuring a small excess risk. Experiments on different tasks consolidate our findings.

Vector-Valued Least-Squares Regression under Output Regularity Assumptions

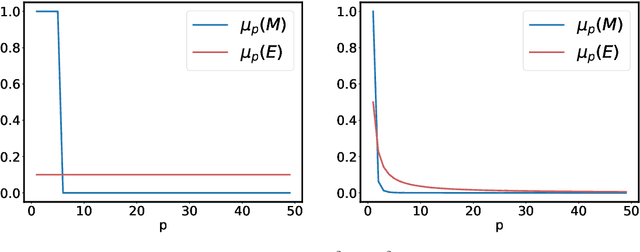
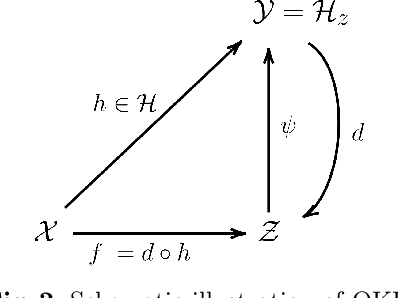
We propose and analyse a reduced-rank method for solving least-squares regression problems with infinite dimensional output. We derive learning bounds for our method, and study under which setting statistical performance is improved in comparison to full-rank method. Our analysis extends the interest of reduced-rank regression beyond the standard low-rank setting to more general output regularity assumptions. We illustrate our theoretical insights on synthetic least-squares problems. Then, we propose a surrogate structured prediction method derived from this reduced-rank method. We assess its benefits on three different problems: image reconstruction, multi-label classification, and metabolite identification.

Learning to Predict Graphs with Fused Gromov-Wasserstein Barycenters

This paper introduces a novel and generic framework to solve the flagship task of supervised labeled graph prediction by leveraging Optimal Transport tools. We formulate the problem as regression with the Fused Gromov-Wasserstein (FGW) loss and propose a predictive model relying on a FGW barycenter whose weights depend on inputs. First we introduce a non-parametric estimator based on kernel ridge regression for which theoretical results such as consistency and excess risk bound are proved. Next we propose an interpretable parametric model where the barycenter weights are modeled with a neural network and the graphs on which the FGW barycenter is calculated are additionally learned. Numerical experiments show the strength of the method and its ability to interpolate in the labeled graph space on simulated data and on a difficult metabolic identification problem where it can reach very good performance with very little engineering.

Learning Output Embeddings in Structured Prediction

A powerful and flexible approach to structured prediction consists in embedding the structured objects to be predicted into a feature space of possibly infinite dimension, and then, solving a regression problem in this output space. A prediction in the original space is computed by solving a pre-image problem. In such an approach, the embedding, linked to the target loss, is defined prior to the learning phase. In this work, we propose to jointly learn an approximation of the output embedding and the regression function into the new feature space. Output Embedding Learning (OEL) allows to leverage a priori information on the outputs and also unexploited unsupervised output data, which are both often available in structured prediction problems. We give a general learning method that we theoretically study in the linear case, proving consistency and excess-risk bound. OEL is tested on various structured prediction problems, showing its versatility and reveals to be especially useful when the training dataset is small compared to the complexity of the task.