Learning Controlled Stochastic Differential Equations

Identification of nonlinear dynamical systems is crucial across various fields, facilitating tasks such as control, prediction, optimization, and fault detection. Many applications require methods capable of handling complex systems while providing strong learning guarantees for safe and reliable performance. However, existing approaches often focus on simplified scenarios, such as deterministic models, known diffusion, discrete systems, one-dimensional dynamics, or systems constrained by strong structural assumptions such as linearity. This work proposes a novel method for estimating both drift and diffusion coefficients of continuous, multidimensional, nonlinear controlled stochastic differential equations with non-uniform diffusion. We assume regularity of the coefficients within a Sobolev space, allowing for broad applicability to various dynamical systems in robotics, finance, climate modeling, and biology. Leveraging the Fokker-Planck equation, we split the estimation into two tasks: (a) estimating system dynamics for a finite set of controls, and (b) estimating coefficients that govern those dynamics. We provide strong theoretical guarantees, including finite-sample bounds for \(L^2\), \(L^\infty\), and risk metrics, with learning rates adaptive to coefficients' regularity, similar to those in nonparametric least-squares regression literature. The practical effectiveness of our approach is demonstrated through extensive numerical experiments. Our method is available as an open-source Python library.

Risk-Averse Trajectory Optimization via Sample Average Approximation

Trajectory optimization under uncertainty underpins a wide range of applications in robotics. However, existing methods are limited in terms of reasoning about sources of epistemic and aleatoric uncertainty, space and time correlations, nonlinear dynamics, and non-convex constraints. In this work, we first introduce a continuous-time planning formulation with an average-value-at-risk constraint over the entire planning horizon. Then, we propose a sample-based approximation that unlocks an efficient, general-purpose, and time-consistent algorithm for risk-averse trajectory optimization. We prove that the method is asymptotically optimal and derive finite-sample error bounds. Simulations demonstrate the high speed and reliability of the approach on problems with stochasticity in nonlinear dynamics, obstacle fields, interactions, and terrain parameters.

Non-Parametric Learning of Stochastic Differential Equations with Fast Rates of Convergence

We propose a novel non-parametric learning paradigm for the identification of drift and diffusion coefficients of non-linear stochastic differential equations, which relies upon discrete-time observations of the state. The key idea essentially consists of fitting a RKHS-based approximation of the corresponding Fokker-Planck equation to such observations, yielding theoretical estimates of learning rates which, unlike previous works, become increasingly tighter when the regularity of the unknown drift and diffusion coefficients becomes higher. Our method being kernel-based, offline pre-processing may in principle be profitably leveraged to enable efficient numerical implementation.

Exact Characterization of the Convex Hulls of Reachable Sets

We study the convex hulls of reachable sets of nonlinear systems with bounded disturbances. Reachable sets play a critical role in control, but remain notoriously challenging to compute, and existing over-approximation tools tend to be conservative or computationally expensive. In this work, we exactly characterize the convex hulls of reachable sets as the convex hulls of solutions of an ordinary differential equation from all possible initial values of the disturbances. This finite-dimensional characterization unlocks a tight estimation algorithm to over-approximate reachable sets that is significantly faster and more accurate than existing methods. We present applications to neural feedback loop analysis and robust model predictive control.

Using Spectral Submanifolds for Nonlinear Periodic Control

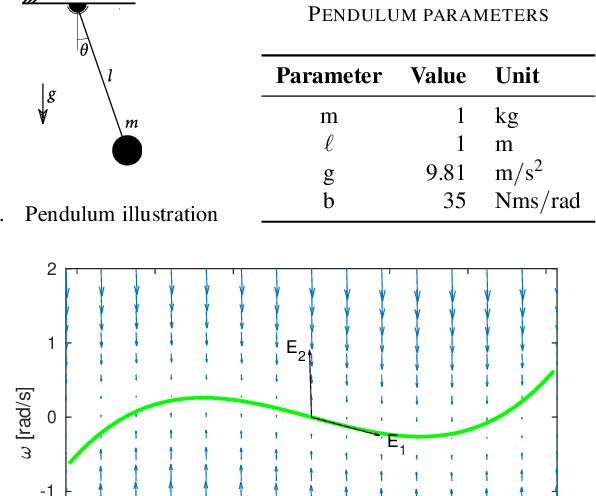
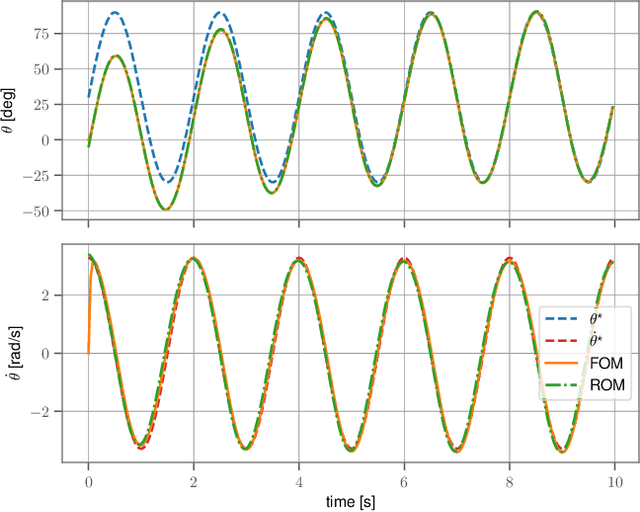
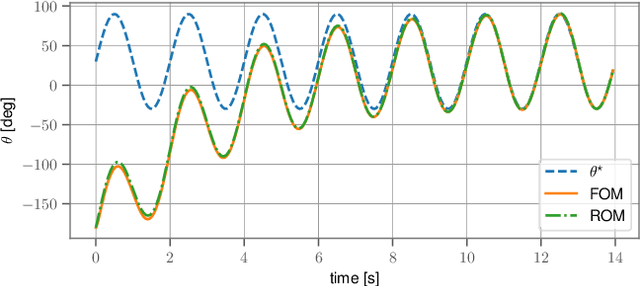
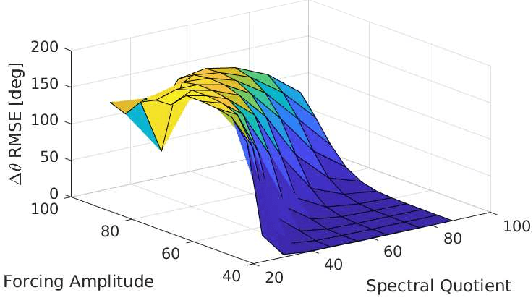
Very high dimensional nonlinear systems arise in many engineering problems due to semi-discretization of the governing partial differential equations, e.g. through finite element methods. The complexity of these systems present computational challenges for direct application to automatic control. While model reduction has seen ubiquitous applications in control, the use of nonlinear model reduction methods in this setting remains difficult. The problem lies in preserving the structure of the nonlinear dynamics in the reduced order model for high-fidelity control. In this work, we leverage recent advances in Spectral Submanifold (SSM) theory to enable model reduction under well-defined assumptions for the purpose of efficiently synthesizing feedback controllers.

A Simple and Efficient Sampling-based Algorithm for General Reachability Analysis

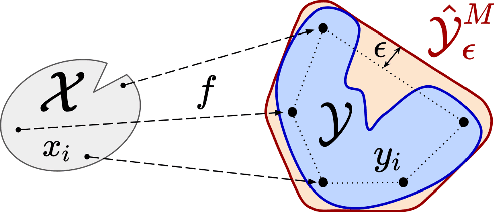
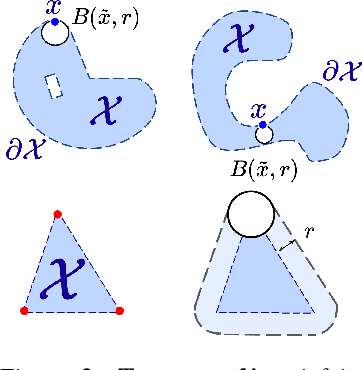
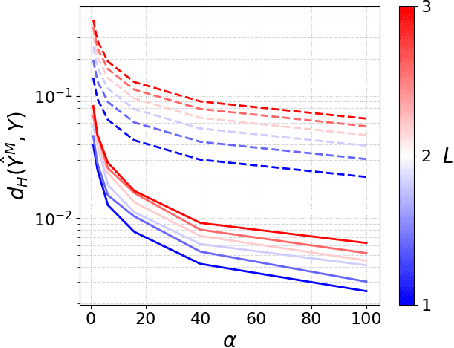
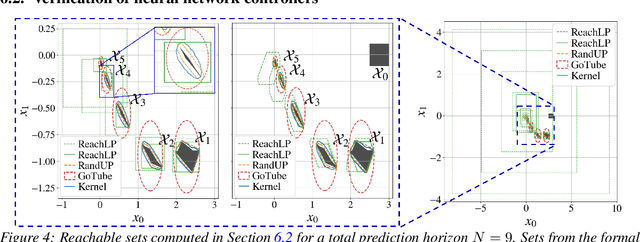
In this work, we analyze an efficient sampling-based algorithm for general-purpose reachability analysis, which remains a notoriously challenging problem with applications ranging from neural network verification to safety analysis of dynamical systems. By sampling inputs, evaluating their images in the true reachable set, and taking their $\epsilon$-padded convex hull as a set estimator, this algorithm applies to general problem settings and is simple to implement. Our main contribution is the derivation of asymptotic and finite-sample accuracy guarantees using random set theory. This analysis informs algorithmic design to obtain an $\epsilon$-close reachable set approximation with high probability, provides insights into which reachability problems are most challenging, and motivates safety-critical applications of the technique. On a neural network verification task, we show that this approach is more accurate and significantly faster than prior work. Informed by our analysis, we also design a robust model predictive controller that we demonstrate in hardware experiments.

Convex Optimization for Trajectory Generation

Reliable and efficient trajectory generation methods are a fundamental need for autonomous dynamical systems of tomorrow. The goal of this article is to provide a comprehensive tutorial of three major convex optimization-based trajectory generation methods: lossless convexification (LCvx), and two sequential convex programming algorithms known as SCvx and GuSTO. In this article, trajectory generation is the computation of a dynamically feasible state and control signal that satisfies a set of constraints while optimizing key mission objectives. The trajectory generation problem is almost always nonconvex, which typically means that it is not readily amenable to efficient and reliable solution onboard an autonomous vehicle. The three algorithms that we discuss use problem reformulation and a systematic algorithmic strategy to nonetheless solve nonconvex trajectory generation tasks through the use of a convex optimizer. The theoretical guarantees and computational speed offered by convex optimization have made the algorithms popular in both research and industry circles. To date, the list of applications includes rocket landing, spacecraft hypersonic reentry, spacecraft rendezvous and docking, aerial motion planning for fixed-wing and quadrotor vehicles, robot motion planning, and more. Among these applications are high-profile rocket flights conducted by organizations like NASA, Masten Space Systems, SpaceX, and Blue Origin. This article aims to give the reader the tools and understanding necessary to work with each algorithm, and to know what each method can and cannot do. A publicly available source code repository supports the provided numerical examples. By the end of the article, the reader should be ready to use the methods, to extend them, and to contribute to their many exciting modern applications.

Composable Geometric Motion Policies using Multi-Task Pullback Bundle Dynamical Systems

Despite decades of work in fast reactive planning and control, challenges remain in developing reactive motion policies on non-Euclidean manifolds and enforcing constraints while avoiding undesirable potential function local minima. This work presents a principled method for designing and fusing desired robot task behaviors into a stable robot motion policy, leveraging the geometric structure of non-Euclidean manifolds, which are prevalent in robot configuration and task spaces. Our Pullback Bundle Dynamical Systems (PBDS) framework drives desired task behaviors and prioritizes tasks using separate position-dependent and position/velocity-dependent Riemannian metrics, respectively, thus simplifying individual task design and modular composition of tasks. For enforcing constraints, we provide a class of metric-based tasks, eliminating local minima by imposing non-conflicting potential functions only for goal region attraction. We also provide a geometric optimization problem for combining tasks inspired by Riemannian Motion Policies (RMPs) that reduces to a simple least-squares problem, and we show that our approach is geometrically well-defined. We demonstrate the PBDS framework on the sphere $\mathbb S^2$ and at 300-500 Hz on a manipulator arm, and we provide task design guidance and an open-source Julia library implementation. Overall, this work presents a fast, easy-to-use framework for generating motion policies without unwanted potential function local minima on general manifolds.

Analysis of Theoretical and Numerical Properties of Sequential Convex Programming for Continuous-Time Optimal Control

Through the years, Sequential Convex Programming (SCP) has gained great interest as an efficient tool for non-convex optimal control. Despite the large number of existing algorithmic frameworks, only a few are accompanied by rigorous convergence analysis, which are often only tailored to discrete-time problem formulations. In this paper, we present a unifying theoretical analysis of a fairly general class of SCP procedures which is applied to the original continuous-time formulation. Besides the extension of classical convergence guarantees to continuous-time settings, our analysis reveals two new features inherited by SCP-type methods. First, we show how one can more easily account for manifold-type constraints, which play a key role in the optimal control of mechanical systems. Second, we demonstrate how the theoretical analysis may be leveraged to devise an accelerated implementation of SCP based on indirect methods. Detailed numerical experiments are provided to show the key benefits of a continuous-time analysis to improve performance.

RRT2.0 for Fast and Optimal Kinodynamic Sampling-Based Motion Planning

We present RRT2.0: a simple yet efficient tree-based planner for asymptotically-optimal motion planning with kinodynamic constraints. RRT2.0 uses forward propagation and does not rely on the availability of a two-point boundary-value solver. The latter is a limiting requirement for some kinodynamic planners that are asymptotically optimal. The proposed approach improves upon a technique by Hauser and Zhou (2016), who explore an augmented state space with an additional coordinate, which endows every point in space with its cost-to-come value. Importantly, our optimality proofs require a milder and easily-verifiable set of assumptions on the problem and system: Lipschitz-continuity of the cost function and the dynamics. In particular, we prove that for any system satisfying those assumptions, any trajectory having a piecewise-constant control function and positive clearance from obstacles can be approximated arbitrarily well by a trajectory found by RRT2.0. We provide experimental results demonstrating on a couple of robot models with kinodynamic constraints that RRT2.0 outperforms the existing alternatives in practice.