Motion Planning for Safe Landing of a Human-Piloted Parafoil

Most skydiving accidents occur during the parafoil-piloting and landing stages and result from human lapses in judgment while piloting the parafoil. Training of novice pilots is protracted due to the lack of functional and easily accessible training simulators. Moreover, work on parafoil trajectory planning suitable for aiding human training remains limited. To bridge this gap, we study the problem of computing safe trajectories for human-piloted parafoil flight and examine how such trajectories fare against human-generated solutions. For the algorithmic part, we adapt the sampling-based motion planner Stable Sparse RRT (SST) by Li et al., to cope with the problem constraints while minimizing the bank angle (control effort) as a proxy for safety. We then compare the computer-generated solutions with data from human-generated parafoil flight, where the algorithm offers a relative cost improvement of 20\%-80\% over the performance of the human pilot. We observe that human pilots tend to, first, close the horizontal distance to the landing area, and then address the vertical gap by spiraling down to the suitable altitude for starting a landing maneuver. The algorithm considered here makes smoother and more gradual descents, arriving at the landing area at the precise altitude necessary for the final approach while maintaining safety constraints. Overall, the study demonstrates the potential of computer-generated guidelines, rather than traditional rules of thumb, which can be integrated into future simulators to train pilots for safer and more cost-effective flights.

Effective Game-Theoretic Motion Planning via Nested Search

To facilitate effective, safe deployment in the real world, individual robots must reason about interactions with other agents, which often occur without explicit communication. Recent work has identified game theory, particularly the concept of Nash Equilibrium (NE), as a key enabler for behavior-aware decision-making. Yet, existing work falls short of fully unleashing the power of game-theoretic reasoning. Specifically, popular optimization-based methods require simplified robot dynamics and tend to get trapped in local minima due to convexification. Other works that rely on payoff matrices suffer from poor scalability due to the explicit enumeration of all possible trajectories. To bridge this gap, we introduce Game-Theoretic Nested Search (GTNS), a novel, scalable, and provably correct approach for computing NEs in general dynamical systems. GTNS efficiently searches the action space of all agents involved, while discarding trajectories that violate the NE constraint (no unilateral deviation) through an inner search over a lower-dimensional space. Our algorithm enables explicit selection among equilibria by utilizing a user-specified global objective, thereby capturing a rich set of realistic interactions. We demonstrate the approach on a variety of autonomous driving and racing scenarios where we achieve solutions in mere seconds on commodity hardware.

Train-Once Plan-Anywhere Kinodynamic Motion Planning via Diffusion Trees

Kinodynamic motion planning is concerned with computing collision-free trajectories while abiding by the robot's dynamic constraints. This critical problem is often tackled using sampling-based planners (SBPs) that explore the robot's high-dimensional state space by constructing a search tree via action propagations. Although SBPs can offer global guarantees on completeness and solution quality, their performance is often hindered by slow exploration due to uninformed action sampling. Learning-based approaches can yield significantly faster runtimes, yet they fail to generalize to out-of-distribution (OOD) scenarios and lack critical guarantees, e.g., safety, thus limiting their deployment on physical robots. We present Diffusion Tree (DiTree): a \emph{provably-generalizable} framework leveraging diffusion policies (DPs) as informed samplers to efficiently guide state-space search within SBPs. DiTree combines DP's ability to model complex distributions of expert trajectories, conditioned on local observations, with the completeness of SBPs to yield \emph{provably-safe} solutions within a few action propagation iterations for complex dynamical systems. We demonstrate DiTree's power with an implementation combining the popular RRT planner with a DP action sampler trained on a \emph{single environment}. In comprehensive evaluations on OOD scenarios, % DiTree has comparable runtimes to a standalone DP (3x faster than classical SBPs), while improving the average success rate over DP and SBPs. DiTree is on average 3x faster than classical SBPs, and outperforms all other approaches by achieving roughly 30\% higher success rate. Project webpage: https://sites.google.com/view/ditree.

Effective Sampling for Robot Motion Planning Through the Lens of Lattices

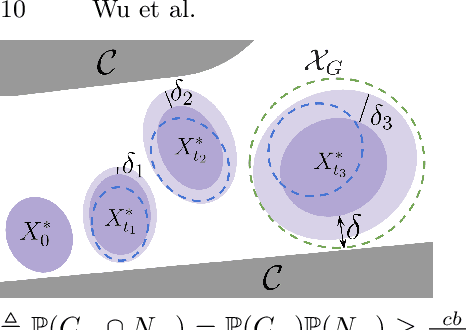
Sampling-based methods for motion planning, which capture the structure of the robot's free space via (typically random) sampling, have gained popularity due to their scalability, simplicity, and for offering global guarantees, such as probabilistic completeness and asymptotic optimality. Unfortunately, the practicality of those guarantees remains limited as they do not provide insights into the behavior of motion planners for a finite number of samples (i.e., a finite running time). In this work, we harness lattice theory and the concept of $(\delta,\epsilon)$-completeness by Tsao et al. (2020) to construct deterministic sample sets that endow their planners with strong finite-time guarantees while minimizing running time. In particular, we introduce a highly-efficient deterministic sampling approach based on the $A_d^*$ lattice, which is the best-known geometric covering in dimensions $\leq 21$. Using our new sampling approach, we obtain at least an order-of-magnitude speedup over existing deterministic and uniform random sampling methods for complex motion-planning problems. Overall, our work provides deep mathematical insights while advancing the practical applicability of sampling-based motion planning.

From Configuration-Space Clearance to Feature-Space Margin: Sample Complexity in Learning-Based Collision Detection

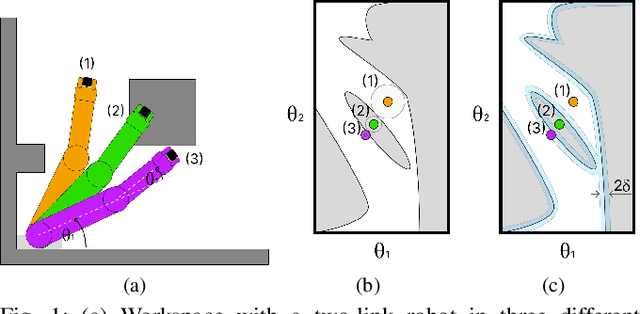
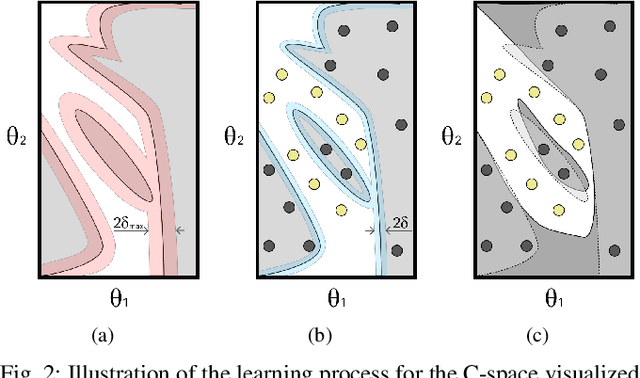
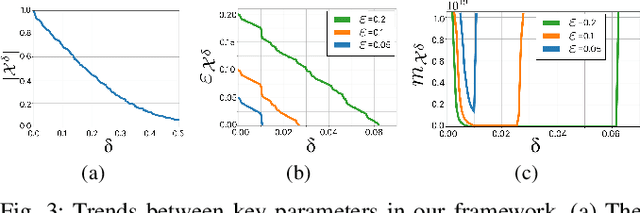
Motion planning is a central challenge in robotics, with learning-based approaches gaining significant attention in recent years. Our work focuses on a specific aspect of these approaches: using machine-learning techniques, particularly Support Vector Machines (SVM), to evaluate whether robot configurations are collision free, an operation termed ``collision detection''. Despite the growing popularity of these methods, there is a lack of theory supporting their efficiency and prediction accuracy. This is in stark contrast to the rich theoretical results of machine-learning methods in general and of SVMs in particular. Our work bridges this gap by analyzing the sample complexity of an SVM classifier for learning-based collision detection in motion planning. We bound the number of samples needed to achieve a specified accuracy at a given confidence level. This result is stated in terms relevant to robot motion-planning such as the system's clearance. Building on these theoretical results, we propose a collision-detection algorithm that can also provide statistical guarantees on the algorithm's error in classifying robot configurations as collision-free or not.

Impossibility of Self-Organized Aggregation without Computation

In their seminal work, Gauci et al. (2014) studied the fundamental task of aggregation, wherein multiple robots need to gather without an a priori agreed-upon meeting location, using minimal hardware. That paper considered differential-drive robots that are memoryless and unable to compute. Moreover, the robots cannot communicate with one another and are only equipped with a simple sensor that determines whether another robot is directly in front of them. Despite those severe limitations, Gauci et al. introduced a controller and proved mathematically that it aggregates a system of two robots for any initial state. Unfortunately, for larger systems, the same controller aggregates empirically in many cases but not all. Thus, the question of whether a controller exists that aggregates for any number of robots remains open. In this paper, we show that no such controller exists by investigating the geometric structure of controllers. In addition, we disprove the aggregation proof of the paper above for two robots and present an alternative controller alongside a simple and rigorous aggregation proof.

Inspection planning under execution uncertainty

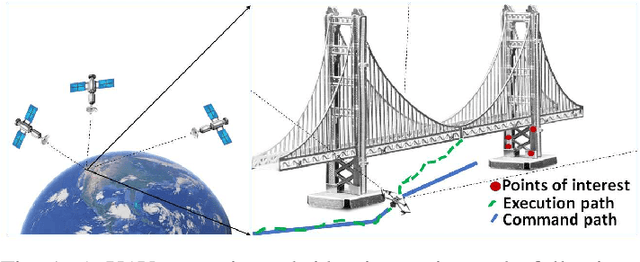
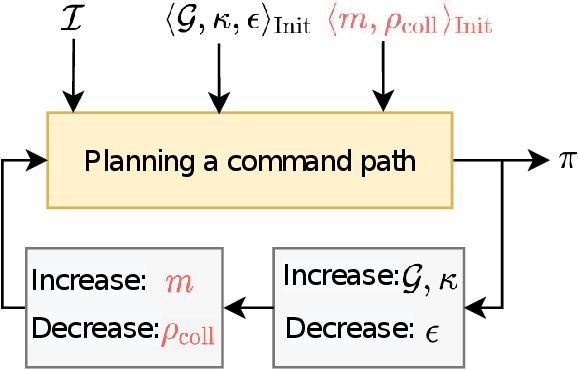
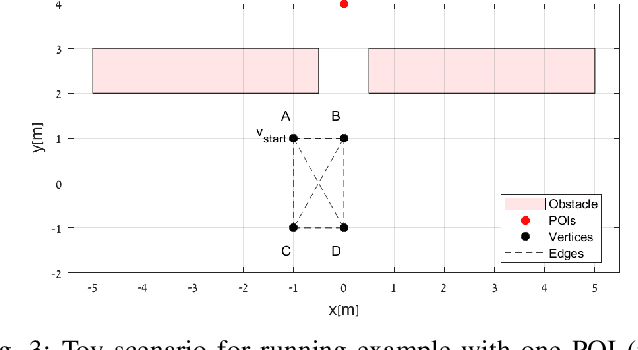
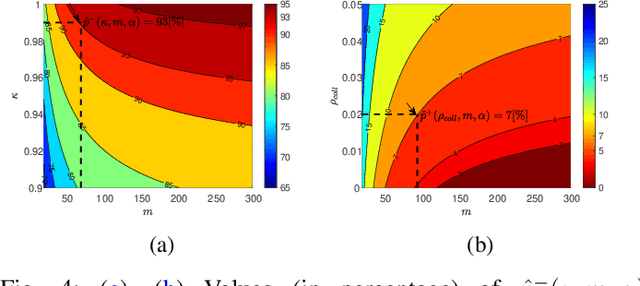
Autonomous inspection tasks necessitate effective path-planning mechanisms to efficiently gather observations from points of interest (POI). However, localization errors commonly encountered in urban environments can introduce execution uncertainty, posing challenges to the successful completion of such tasks. To tackle these challenges, we present IRIS-under uncertainty (IRIS-U^2), an extension of the incremental random inspection-roadmap search (IRIS) algorithm, that addresses the offline planning problem via an A*-based approach, where the planning process occurs prior the online execution. The key insight behind IRIS-U^2 is transforming the computed localization uncertainty, obtained through Monte Carlo (MC) sampling, into a POI probability. IRIS-U^2 offers insights into the expected performance of the execution task by providing confidence intervals (CI) for the expected coverage, expected path length, and collision probability, which becomes progressively tighter as the number of MC samples increase. The efficacy of IRIS-U^2 is demonstrated through a case study focusing on structural inspections of bridges. Our approach exhibits improved expected coverage, reduced collision probability, and yields increasingly-precise CIs as the number of MC samples grows. Furthermore, we emphasize the potential advantages of computing bounded sub-optimal solutions to reduce computation time while still maintaining the same CI boundaries.

Terraforming -- Environment Manipulation during Disruptions for Multi-Agent Pickup and Delivery

In automated warehouses, teams of mobile robots fulfill the packaging process by transferring inventory pods to designated workstations while navigating narrow aisles formed by tightly packed pods. This problem is typically modeled as a Multi-Agent Pickup and Delivery (MAPD) problem, which is then solved by repeatedly planning collision-free paths for agents on a fixed graph, as in the Rolling-Horizon Collision Resolution (RHCR) algorithm. However, existing approaches make the limiting assumption that agents are only allowed to move pods that correspond to their current task, while considering the other pods as stationary obstacles (even though all pods are movable). This behavior can result in unnecessarily long paths which could otherwise be avoided by opening additional corridors via pod manipulation. To this end, we explore the implications of allowing agents the flexibility of dynamically relocating pods. We call this new problem Terraforming MAPD (tMAPD) and develop an RHCR-based approach to tackle it. As the extra flexibility of terraforming comes at a significant computational cost, we utilize this capability judiciously by identifying situations where it could make a significant impact on the solution quality. In particular, we invoke terraforming in response to disruptions that often occur in automated warehouses, e.g., when an item is dropped from a pod or when agents malfunction. Empirically, using our approach for tMAPD, where disruptions are modeled via a stochastic process, we improve throughput by over 10%, reduce the maximum service time (the difference between the drop-off time and the pickup time of a pod) by more than 50%, without drastically increasing the runtime, compared to the MAPD setting.

Robust-RRT: Probabilistically-Complete Motion Planning for Uncertain Nonlinear Systems

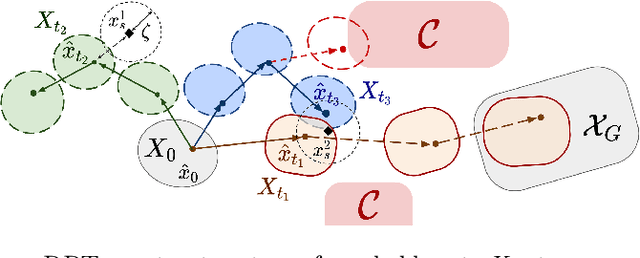
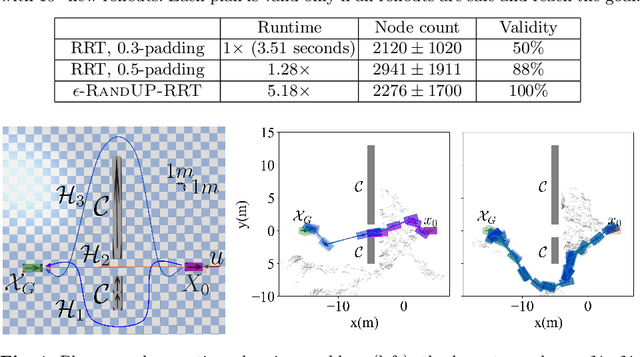
Robust motion planning entails computing a global motion plan that is safe under all possible uncertainty realizations, be it in the system dynamics, the robot's initial position, or with respect to external disturbances. Current approaches for robust motion planning either lack theoretical guarantees, or make restrictive assumptions on the system dynamics and uncertainty distributions. In this paper, we address these limitations by proposing the robust rapidly-exploring random-tree (Robust-RRT) algorithm, which integrates forward reachability analysis directly into sampling-based control trajectory synthesis. We prove that Robust-RRT is probabilistically complete (PC) for nonlinear Lipschitz continuous dynamical systems with bounded uncertainty. In other words, Robust-RRT eventually finds a robust motion plan that is feasible under all possible uncertainty realizations assuming such a plan exists. Our analysis applies even to unstable systems that admit only short-horizon feasible plans; this is because we explicitly consider the time evolution of reachable sets along control trajectories. Thanks to the explicit consideration of time dependency in our analysis, PC applies to unstabilizable systems. To the best of our knowledge, this is the most general PC proof for robust sampling-based motion planning, in terms of the types of uncertainties and dynamical systems it can handle. Considering that an exact computation of reachable sets can be computationally expensive for some dynamical systems, we incorporate sampling-based reachability analysis into Robust-RRT and demonstrate our robust planner on nonlinear, underactuated, and hybrid systems.

Multi-Agent Terraforming: Efficient Multi-Agent Path Finding via Environment Manipulation

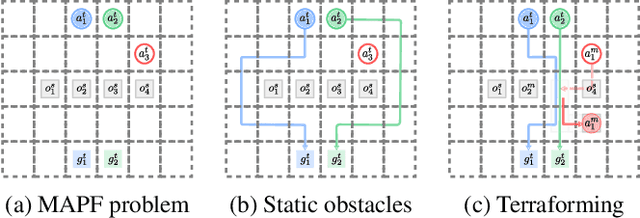
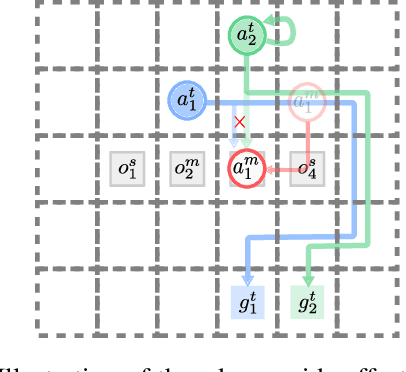
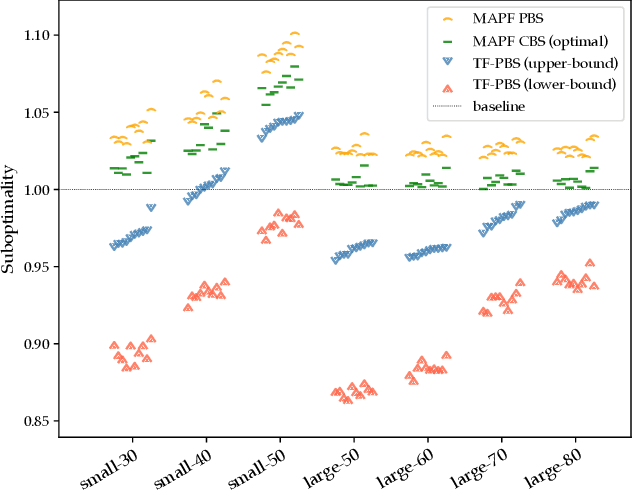
Multi-agent pathfinding (MAPF) is concerned with planning collision-free paths for a team of agents from their start to goal locations in an environment cluttered with obstacles. Typical approaches for MAPF consider the locations of obstacles as being fixed, which limits their effectiveness in automated warehouses, where obstacles (representing pods or shelves) can be moved out of the way by agents (representing robots) to relieve bottlenecks and introduce shorter routes. In this work we initiate the study of MAPF with movable obstacles. In particular, we introduce a new extension of MAPF, which we call Terraforming MAPF (tMAPF), where some agents are responsible for moving obstacles to clear the way for other agents. Solving tMAPF is extremely challenging as it requires reasoning not only about collisions between agents, but also where and when obstacles should be moved. We present extensions of two state-of-the-art algorithms, CBS and PBS, in order to tackle tMAPF, and demonstrate that they can consistently outperform the best solution possible under a static-obstacle setting.