First, Learn What You Don't Know: Active Information Gathering for Driving at the Limits of Handling

Combining data-driven models that adapt online and model predictive control (MPC) has enabled effective control of nonlinear systems. However, when deployed on unstable systems, online adaptation may not be fast enough to ensure reliable simultaneous learning and control. For example, controllers on a vehicle executing highly dynamic maneuvers may push the tires to their friction limits, destabilizing the vehicle and allowing modeling errors to quickly compound and cause a loss of control. In this work, we present a Bayesian meta-learning MPC framework. We propose an expressive vehicle dynamics model that leverages Bayesian last-layer meta-learning to enable rapid online adaptation. The model's uncertainty estimates are used to guide informative data collection and quickly improve the model prior to deployment. Experiments on a Toyota Supra show that (i) the framework enables reliable control in dynamic drifting maneuvers, (ii) online adaptation alone may not suffice for zero-shot control of a vehicle at the edge of stability, and (iii) active data collection helps achieve reliable performance.

Risk-Averse Model Predictive Control for Racing in Adverse Conditions

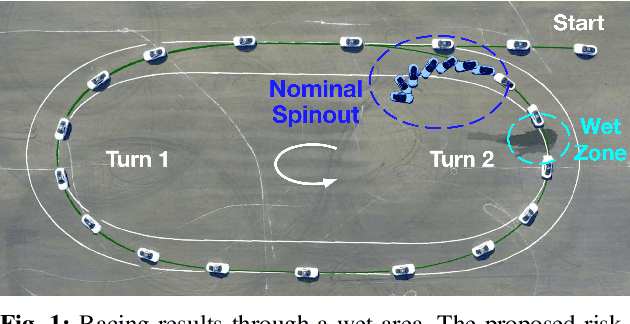
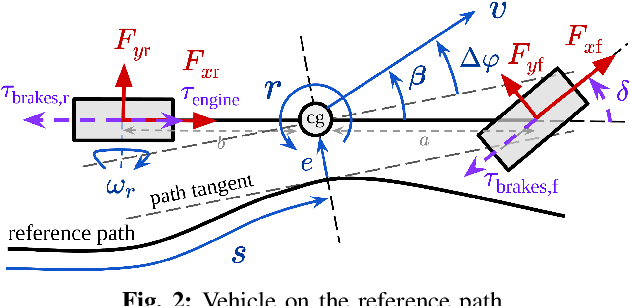
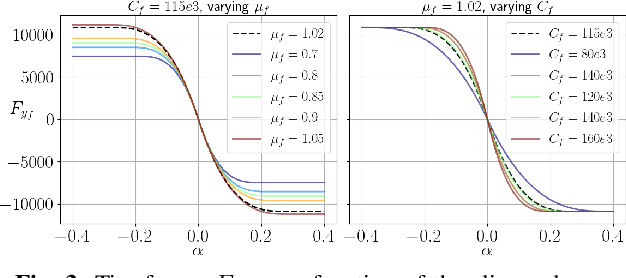
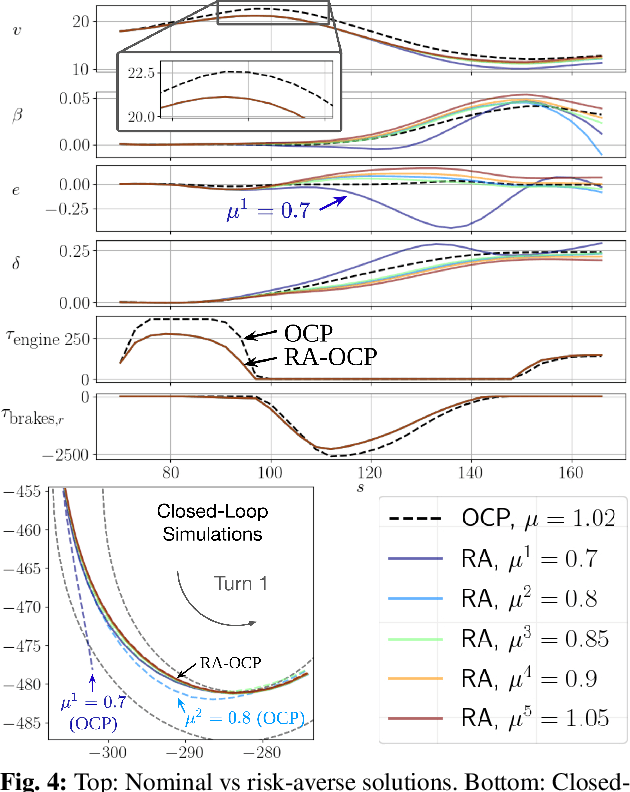
Model predictive control (MPC) algorithms can be sensitive to model mismatch when used in challenging nonlinear control tasks. In particular, the performance of MPC for vehicle control at the limits of handling suffers when the underlying model overestimates the vehicle's capabilities. In this work, we propose a risk-averse MPC framework that explicitly accounts for uncertainty over friction limits and tire parameters. Our approach leverages a sample-based approximation of an optimal control problem with a conditional value at risk (CVaR) constraint. This sample-based formulation enables planning with a set of expressive vehicle dynamics models using different tire parameters. Moreover, this formulation enables efficient numerical resolution via sequential quadratic programming and GPU parallelization. Experiments on a Lexus LC 500 show that risk-averse MPC unlocks reliable performance, while a deterministic baseline that plans using a single dynamics model may lose control of the vehicle in adverse road conditions.

Risk-Averse Trajectory Optimization via Sample Average Approximation

Trajectory optimization under uncertainty underpins a wide range of applications in robotics. However, existing methods are limited in terms of reasoning about sources of epistemic and aleatoric uncertainty, space and time correlations, nonlinear dynamics, and non-convex constraints. In this work, we first introduce a continuous-time planning formulation with an average-value-at-risk constraint over the entire planning horizon. Then, we propose a sample-based approximation that unlocks an efficient, general-purpose, and time-consistent algorithm for risk-averse trajectory optimization. We prove that the method is asymptotically optimal and derive finite-sample error bounds. Simulations demonstrate the high speed and reliability of the approach on problems with stochasticity in nonlinear dynamics, obstacle fields, interactions, and terrain parameters.

Exact Characterization of the Convex Hulls of Reachable Sets

We study the convex hulls of reachable sets of nonlinear systems with bounded disturbances. Reachable sets play a critical role in control, but remain notoriously challenging to compute, and existing over-approximation tools tend to be conservative or computationally expensive. In this work, we exactly characterize the convex hulls of reachable sets as the convex hulls of solutions of an ordinary differential equation from all possible initial values of the disturbances. This finite-dimensional characterization unlocks a tight estimation algorithm to over-approximate reachable sets that is significantly faster and more accurate than existing methods. We present applications to neural feedback loop analysis and robust model predictive control.

A System-Level View on Out-of-Distribution Data in Robotics

When testing conditions differ from those represented in training data, so-called out-of-distribution (OOD) inputs can mar the reliability of black-box learned components in the modern robot autonomy stack. Therefore, coping with OOD data is an important challenge on the path towards trustworthy learning-enabled open-world autonomy. In this paper, we aim to demystify the topic of OOD data and its associated challenges in the context of data-driven robotic systems, drawing connections to emerging paradigms in the ML community that study the effect of OOD data on learned models in isolation. We argue that as roboticists, we should reason about the overall system-level competence of a robot as it performs tasks in OOD conditions. We highlight key research questions around this system-level view of OOD problems to guide future research toward safe and reliable learning-enabled autonomy.

Robotic Table Wiping via Reinforcement Learning and Whole-body Trajectory Optimization

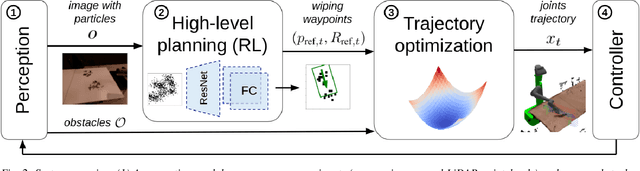
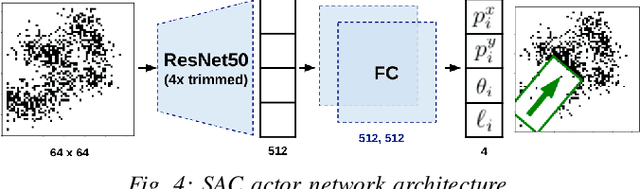
We propose a framework to enable multipurpose assistive mobile robots to autonomously wipe tables to clean spills and crumbs. This problem is challenging, as it requires planning wiping actions while reasoning over uncertain latent dynamics of crumbs and spills captured via high-dimensional visual observations. Simultaneously, we must guarantee constraints satisfaction to enable safe deployment in unstructured cluttered environments. To tackle this problem, we first propose a stochastic differential equation to model crumbs and spill dynamics and absorption with a robot wiper. Using this model, we train a vision-based policy for planning wiping actions in simulation using reinforcement learning (RL). To enable zero-shot sim-to-real deployment, we dovetail the RL policy with a whole-body trajectory optimization framework to compute base and arm joint trajectories that execute the desired wiping motions while guaranteeing constraints satisfaction. We extensively validate our approach in simulation and on hardware. Video: https://youtu.be/inORKP4F3EI

Robust-RRT: Probabilistically-Complete Motion Planning for Uncertain Nonlinear Systems

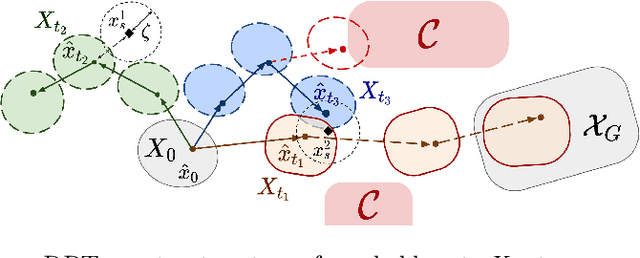
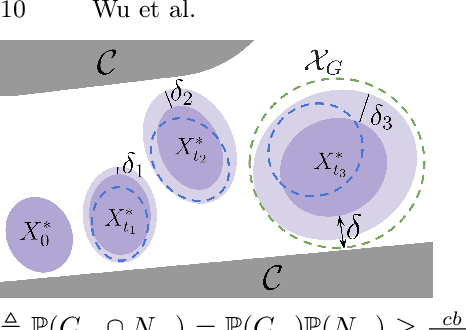
Robust motion planning entails computing a global motion plan that is safe under all possible uncertainty realizations, be it in the system dynamics, the robot's initial position, or with respect to external disturbances. Current approaches for robust motion planning either lack theoretical guarantees, or make restrictive assumptions on the system dynamics and uncertainty distributions. In this paper, we address these limitations by proposing the robust rapidly-exploring random-tree (Robust-RRT) algorithm, which integrates forward reachability analysis directly into sampling-based control trajectory synthesis. We prove that Robust-RRT is probabilistically complete (PC) for nonlinear Lipschitz continuous dynamical systems with bounded uncertainty. In other words, Robust-RRT eventually finds a robust motion plan that is feasible under all possible uncertainty realizations assuming such a plan exists. Our analysis applies even to unstable systems that admit only short-horizon feasible plans; this is because we explicitly consider the time evolution of reachable sets along control trajectories. Thanks to the explicit consideration of time dependency in our analysis, PC applies to unstabilizable systems. To the best of our knowledge, this is the most general PC proof for robust sampling-based motion planning, in terms of the types of uncertainties and dynamical systems it can handle. Considering that an exact computation of reachable sets can be computationally expensive for some dynamical systems, we incorporate sampling-based reachability analysis into Robust-RRT and demonstrate our robust planner on nonlinear, underactuated, and hybrid systems.

Data-Driven Chance Constrained Control using Kernel Distribution Embeddings

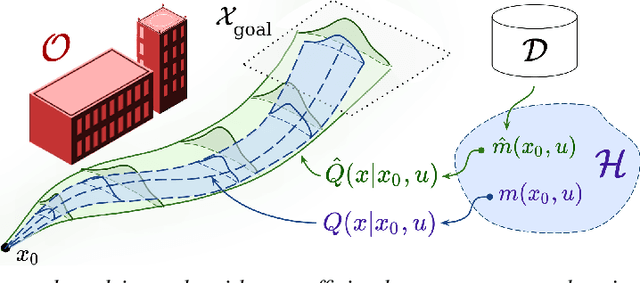
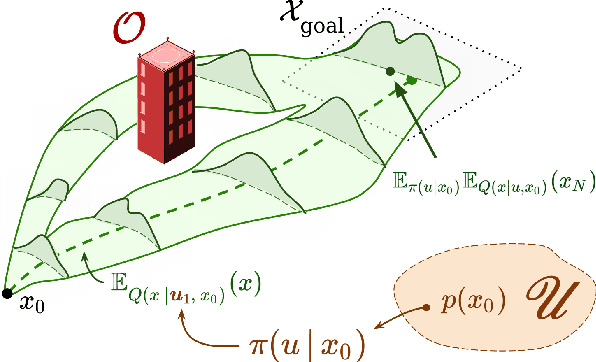
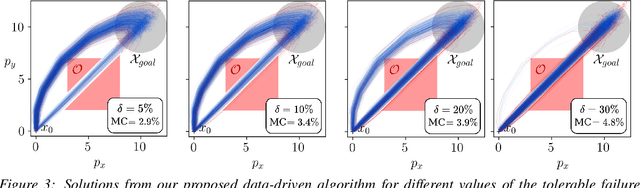
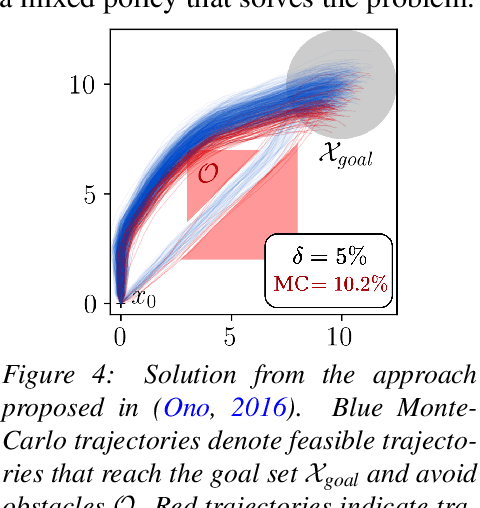
We present a data-driven algorithm for efficiently computing stochastic control policies for general joint chance constrained optimal control problems. Our approach leverages the theory of kernel distribution embeddings, which allows representing expectation operators as inner products in a reproducing kernel Hilbert space. This framework enables approximately reformulating the original problem using a dataset of observed trajectories from the system without imposing prior assumptions on the parameterization of the system dynamics or the structure of the uncertainty. By optimizing over a finite subset of stochastic open-loop control trajectories, we relax the original problem to a linear program over the control parameters that can be efficiently solved using standard convex optimization techniques. We demonstrate our proposed approach in simulation on a system with nonlinear non-Markovian dynamics navigating in a cluttered environment.

A Simple and Efficient Sampling-based Algorithm for General Reachability Analysis

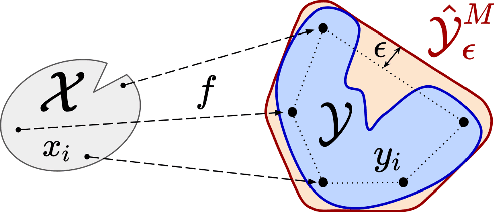
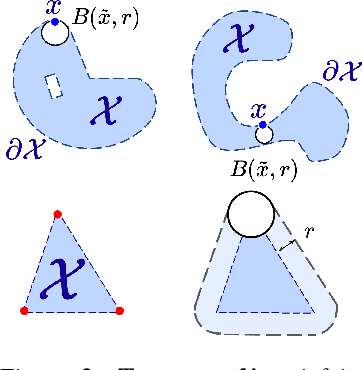
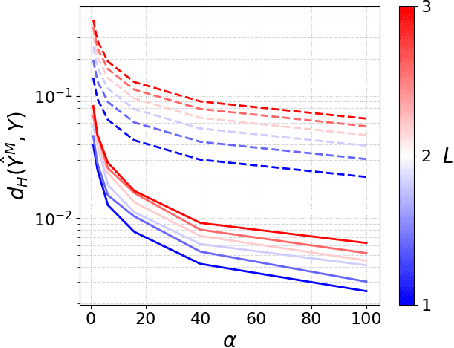
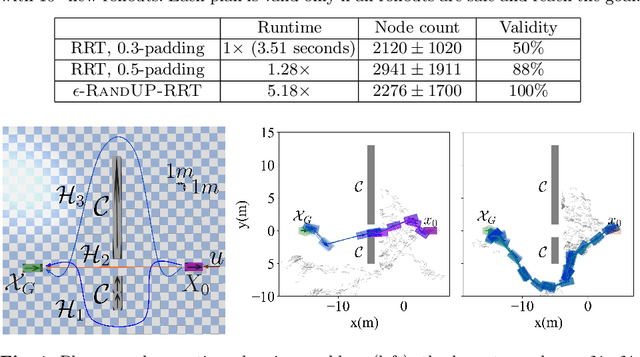
In this work, we analyze an efficient sampling-based algorithm for general-purpose reachability analysis, which remains a notoriously challenging problem with applications ranging from neural network verification to safety analysis of dynamical systems. By sampling inputs, evaluating their images in the true reachable set, and taking their $\epsilon$-padded convex hull as a set estimator, this algorithm applies to general problem settings and is simple to implement. Our main contribution is the derivation of asymptotic and finite-sample accuracy guarantees using random set theory. This analysis informs algorithmic design to obtain an $\epsilon$-close reachable set approximation with high probability, provides insights into which reachability problems are most challenging, and motivates safety-critical applications of the technique. On a neural network verification task, we show that this approach is more accurate and significantly faster than prior work. Informed by our analysis, we also design a robust model predictive controller that we demonstrate in hardware experiments.

On the Problem of Reformulating Systems with Uncertain Dynamics as a Stochastic Differential Equation

We identify an issue in recent approaches to learning-based control that reformulate systems with uncertain dynamics using a stochastic differential equation. Specifically, we discuss the approximation that replaces a model with fixed but uncertain parameters (a source of epistemic uncertainty) with a model subject to external disturbances modeled as a Brownian motion (corresponding to aleatoric uncertainty).