Generalized-CVO: Fast and Correspondence-Free Local Point Cloud Registration with Second Order Riemannian Optimization

We propose a fast and correspondence-free local point cloud registration method that leverages geometric surface structure and reproducing kernel Hilbert space (RKHS) embeddings. The method represents point clouds as continuous functions with point-wise anisotropic kernels that encode local geometry. This formulation improves alignment along surface normals while relaxing alignment along tangential directions. To solve the resulting registration problem, we propose a second-order on-manifold optimization scheme with approximate Riemannian Hessians, achieving a speedup of up to 10x over the first-order solvers used in prior correspondence-free RKHS-based methods. We demonstrate improved frame-to-frame LiDAR and RGB-D tracking accuracy across diverse indoor and outdoor datasets. On a LiDAR tracking registration task in the driving domain, we achieve a reduction of $>55\%$ in both translational and rotational drift in challenging feature-sparse environments. On object registration benchmarks, we show improved robustness over ICP-based methods and further gains when refining global initialization, particularly under moderate misalignment.

Boundary Sampling to Learn Predictive Safety Filters via Pontryagin's Maximum Principle

Safety filters provide a practical approach for enforcing safety constraints in autonomous systems. While learning-based tools scale to high-dimensional systems, their performance depends on informative data that includes states likely to lead to constraint violation, which can be difficult to efficiently sample in complex, high-dimensional systems. In this work, we characterize trajectories that barely avoid safety violations using the Pontryagin Maximum Principle. These boundary trajectories are used to guide data collection for learned Hamilton-Jacobi Reachability, concentrating learning efforts near safety-critical states to improve efficiency. The learned Control Barrier Value Function is then used directly for safety filtering. Simulations and experimental validation on a shared-control automotive racing application demonstrate PMP sampling improves learning efficiency, yielding faster convergence, reduced failure rates, and improved safe set reconstruction, with wall times around 3ms.

Vision-Conditioned Variational Bayesian Last Layer Dynamics Models

Agile control of robotic systems often requires anticipating how the environment affects system behavior. For example, a driver must perceive the road ahead to anticipate available friction and plan actions accordingly. Achieving such proactive adaptation within autonomous frameworks remains a challenge, particularly under rapidly changing conditions. Traditional modeling approaches often struggle to capture abrupt variations in system behavior, while adaptive methods are inherently reactive and may adapt too late to ensure safety. We propose a vision-conditioned variational Bayesian last-layer dynamics model that leverages visual context to anticipate changes in the environment. The model first learns nominal vehicle dynamics and is then fine-tuned with feature-wise affine transformations of latent features, enabling context-aware dynamics prediction. The resulting model is integrated into an optimal controller for vehicle racing. We validate our method on a Lexus LC500 racing through water puddles. With vision-conditioning, the system completed all 12 attempted laps under varying conditions. In contrast, all baselines without visual context consistently lost control, demonstrating the importance of proactive dynamics adaptation in high-performance applications.

Semantic Property Maps for Driving Applications

We consider the problem of estimating the parameters of a vehicle dynamics model for predictive control in driving applications. Instead of solely using the instantaneous parameters estimated from the vehicle signals, we combine this with cameras and update a probabilistic map with parameter estimates and semantic information using Bayesian moment matching. Key to this approach is the map representation, which is constructed with conjugate priors to the measurement likelihoods and defined in the same path coordinates as the vehicle controller, such that the map can be externalized to provide a local representation of the parameter likelihoods that vary in space. The result is a spatial map of vehicle parameters adapted online to enhance the driving control system. We provide theoretical guarantees on the smoothness of relevant parameter likelihood statistics as a function of space, which is critical for their use in predictive control.

Towards an Autonomous Test Driver: High-Performance Driver Modeling via Reinforcement Learning

Success in racing requires a unique combination of vehicle setup, understanding of the racetrack, and human expertise. Since building and testing many different vehicle configurations in the real world is prohibitively expensive, high-fidelity simulation is a critical part of racecar development. However, testing different vehicle configurations still requires expert human input in order to evaluate their performance on different racetracks. In this work, we present the first steps towards an autonomous test driver, trained using deep reinforcement learning, capable of evaluating changes in vehicle setup on racing performance while driving at the level of the best human drivers. In addition, the autonomous driver model can be tuned to exhibit more human-like behavioral patterns by incorporating imitation learning into the RL training process. This extension permits the possibility of driver-specific vehicle setup optimization.

First, Learn What You Don't Know: Active Information Gathering for Driving at the Limits of Handling

Combining data-driven models that adapt online and model predictive control (MPC) has enabled effective control of nonlinear systems. However, when deployed on unstable systems, online adaptation may not be fast enough to ensure reliable simultaneous learning and control. For example, controllers on a vehicle executing highly dynamic maneuvers may push the tires to their friction limits, destabilizing the vehicle and allowing modeling errors to quickly compound and cause a loss of control. In this work, we present a Bayesian meta-learning MPC framework. We propose an expressive vehicle dynamics model that leverages Bayesian last-layer meta-learning to enable rapid online adaptation. The model's uncertainty estimates are used to guide informative data collection and quickly improve the model prior to deployment. Experiments on a Toyota Supra show that (i) the framework enables reliable control in dynamic drifting maneuvers, (ii) online adaptation alone may not suffice for zero-shot control of a vehicle at the edge of stability, and (iii) active data collection helps achieve reliable performance.

Reference-Free Formula Drift with Reinforcement Learning: From Driving Data to Tire Energy-Inspired, Real-World Policies

The skill to drift a car--i.e., operate in a state of controlled oversteer like professional drivers--could give future autonomous cars maximum flexibility when they need to retain control in adverse conditions or avoid collisions. We investigate real-time drifting strategies that put the car where needed while bypassing expensive trajectory optimization. To this end, we design a reinforcement learning agent that builds on the concept of tire energy absorption to autonomously drift through changing and complex waypoint configurations while safely staying within track bounds. We achieve zero-shot deployment on the car by training the agent in a simulation environment built on top of a neural stochastic differential equation vehicle model learned from pre-collected driving data. Experiments on a Toyota GR Supra and Lexus LC 500 show that the agent is capable of drifting smoothly through varying waypoint configurations with tracking error as low as 10 cm while stably pushing the vehicles to sideslip angles of up to 63{\deg}.

Risk-Averse Model Predictive Control for Racing in Adverse Conditions

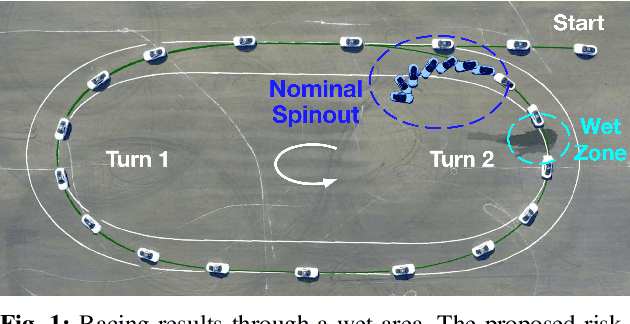
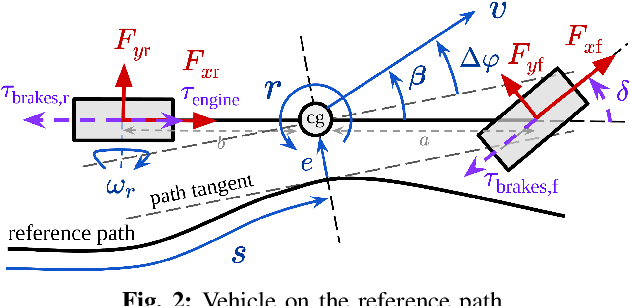
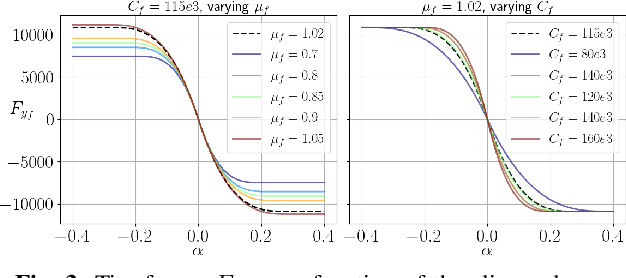
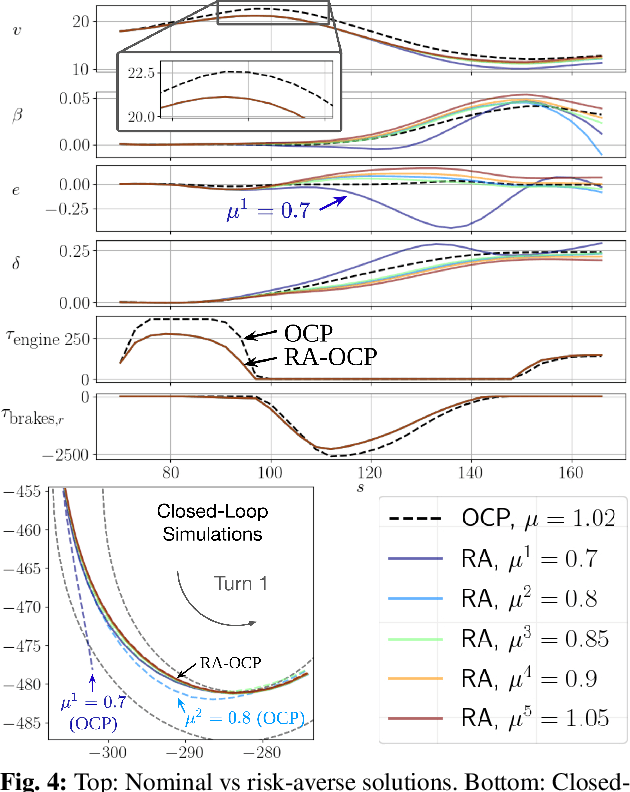
Model predictive control (MPC) algorithms can be sensitive to model mismatch when used in challenging nonlinear control tasks. In particular, the performance of MPC for vehicle control at the limits of handling suffers when the underlying model overestimates the vehicle's capabilities. In this work, we propose a risk-averse MPC framework that explicitly accounts for uncertainty over friction limits and tire parameters. Our approach leverages a sample-based approximation of an optimal control problem with a conditional value at risk (CVaR) constraint. This sample-based formulation enables planning with a set of expressive vehicle dynamics models using different tire parameters. Moreover, this formulation enables efficient numerical resolution via sequential quadratic programming and GPU parallelization. Experiments on a Lexus LC 500 show that risk-averse MPC unlocks reliable performance, while a deterministic baseline that plans using a single dynamics model may lose control of the vehicle in adverse road conditions.

A Sequential Two-Step Algorithm for Fast Generation of Vehicle Racing Trajectories

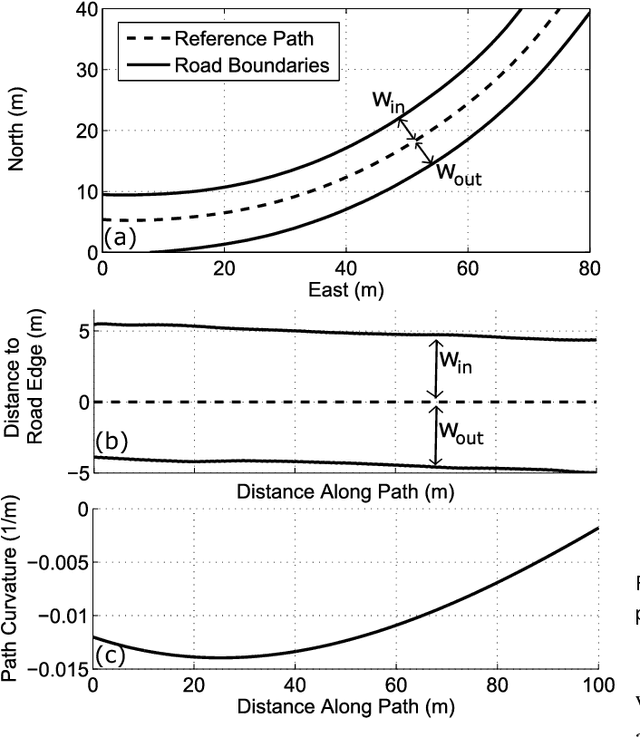
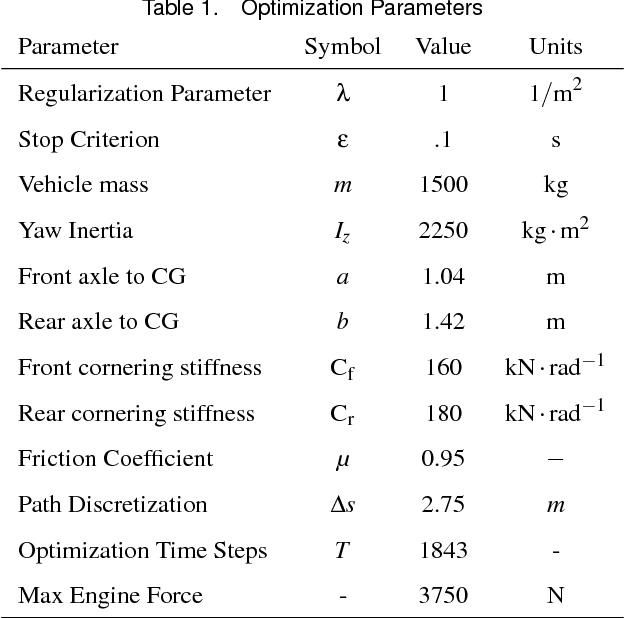
The problem of maneuvering a vehicle through a race course in minimum time requires computation of both longitudinal (brake and throttle) and lateral (steering wheel) control inputs. Unfortunately, solving the resulting nonlinear optimal control problem is typically computationally expensive and infeasible for real-time trajectory planning. This paper presents an iterative algorithm that divides the path generation task into two sequential subproblems that are significantly easier to solve. Given an initial path through the race track, the algorithm runs a forward-backward integration scheme to determine the minimum-time longitudinal speed profile, subject to tire friction constraints. With this fixed speed profile, the algorithm updates the vehicle's path by solving a convex optimization problem that minimizes the resulting path curvature while staying within track boundaries and obeying affine, time-varying vehicle dynamics constraints. This two-step process is repeated iteratively until the predicted lap time no longer improves. While providing no guarantees of convergence or a globally optimal solution, the approach performs very well when validated on the Thunderhill Raceway course in Willows, CA. The predicted lap time converges after four to five iterations, with each iteration over the full 4.5 km race course requiring only thirty seconds of computation time on a laptop computer. The resulting trajectory is experimentally driven at the race circuit with an autonomous Audi TTS test vehicle, and the resulting lap time and racing line is comparable to both a nonlinear gradient descent solution and a trajectory recorded from a professional racecar driver. The experimental results indicate that the proposed method is a viable option for online trajectory planning in the near future.