First, Learn What You Don't Know: Active Information Gathering for Driving at the Limits of Handling

Combining data-driven models that adapt online and model predictive control (MPC) has enabled effective control of nonlinear systems. However, when deployed on unstable systems, online adaptation may not be fast enough to ensure reliable simultaneous learning and control. For example, controllers on a vehicle executing highly dynamic maneuvers may push the tires to their friction limits, destabilizing the vehicle and allowing modeling errors to quickly compound and cause a loss of control. In this work, we present a Bayesian meta-learning MPC framework. We propose an expressive vehicle dynamics model that leverages Bayesian last-layer meta-learning to enable rapid online adaptation. The model's uncertainty estimates are used to guide informative data collection and quickly improve the model prior to deployment. Experiments on a Toyota Supra show that (i) the framework enables reliable control in dynamic drifting maneuvers, (ii) online adaptation alone may not suffice for zero-shot control of a vehicle at the edge of stability, and (iii) active data collection helps achieve reliable performance.

Proximal Gradient Dynamics: Monotonicity, Exponential Convergence, and Applications

In this letter, we study the proximal gradient dynamics. This recently-proposed continuous-time dynamics solves optimization problems whose cost functions are separable into a nonsmooth convex and a smooth component. First, we show that the cost function decreases monotonically along the trajectories of the proximal gradient dynamics. We then introduce a new condition that guarantees exponential convergence of the cost function to its optimal value, and show that this condition implies the proximal Polyak-{\L}ojasiewicz condition. We also show that the proximal Polyak-{\L}ojasiewicz condition guarantees exponential convergence of the cost function. Moreover, we extend these results to time-varying optimization problems, providing bounds for equilibrium tracking. Finally, we discuss applications of these findings, including the LASSO problem, quadratic optimization with polytopic constraints, and certain matrix based problems.

Learning Neural Contracting Dynamics: Extended Linearization and Global Guarantees

Global stability and robustness guarantees in learned dynamical systems are essential to ensure well-behavedness of the systems in the face of uncertainty. We present Extended Linearized Contracting Dynamics (ELCD), the first neural network-based dynamical system with global contractivity guarantees in arbitrary metrics. The key feature of ELCD is a parametrization of the extended linearization of the nonlinear vector field. In its most basic form, ELCD is guaranteed to be (i) globally exponentially stable, (ii) equilibrium contracting, and (iii) globally contracting with respect to some metric. To allow for contraction with respect to more general metrics in the data space, we train diffeomorphisms between the data space and a latent space and enforce contractivity in the latent space, which ensures global contractivity in the data space. We demonstrate the performance of ELCD on the $2$D, $4$D, and $8$D LASA datasets.

Contracting Dynamics for Time-Varying Convex Optimization

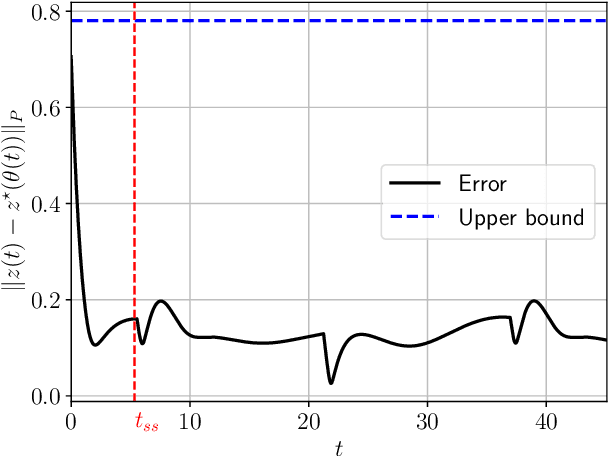
In this article, we provide a novel and broadly-applicable contraction-theoretic approach to continuous-time time-varying convex optimization. For any parameter-dependent contracting dynamics, we show that the tracking error between any solution trajectory and the equilibrium trajectory is uniformly upper bounded in terms of the contraction rate, the Lipschitz constant in which the parameter appears, and the rate of change of the parameter. To apply this result to time-varying convex optimization problems, we establish the strong infinitesimal contraction of dynamics solving three canonical problems, namely monotone inclusions, linear equality-constrained problems, and composite minimization problems. For each of these problems, we prove the sharpest-known rates of contraction and provide explicit tracking error bounds between solution trajectories and minimizing trajectories. We validate our theoretical results on two numerical examples.

Robust Training and Verification of Implicit Neural Networks: A Non-Euclidean Contractive Approach

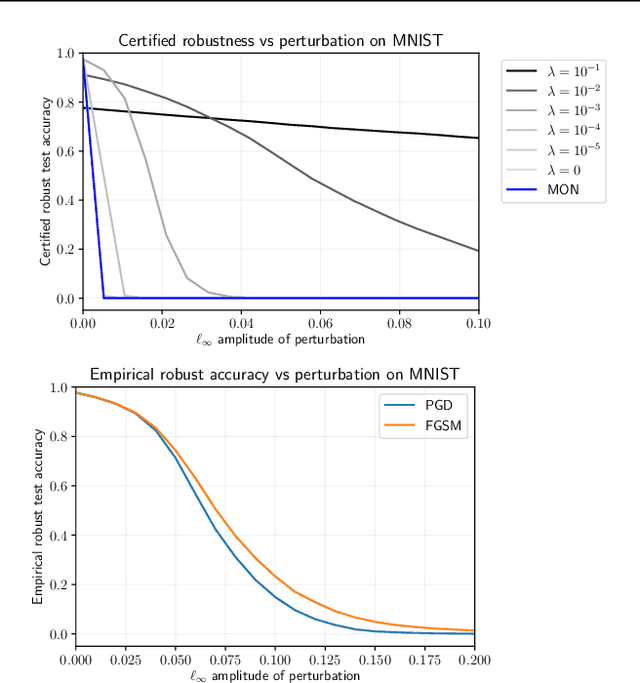
This paper proposes a theoretical and computational framework for training and robustness verification of implicit neural networks based upon non-Euclidean contraction theory. The basic idea is to cast the robustness analysis of a neural network as a reachability problem and use (i) the $\ell_{\infty}$-norm input-output Lipschitz constant and (ii) the tight inclusion function of the network to over-approximate its reachable sets. First, for a given implicit neural network, we use $\ell_{\infty}$-matrix measures to propose sufficient conditions for its well-posedness, design an iterative algorithm to compute its fixed points, and provide upper bounds for its $\ell_\infty$-norm input-output Lipschitz constant. Second, we introduce a related embedded network and show that the embedded network can be used to provide an $\ell_\infty$-norm box over-approximation of the reachable sets of the original network. Moreover, we use the embedded network to design an iterative algorithm for computing the upper bounds of the original system's tight inclusion function. Third, we use the upper bounds of the Lipschitz constants and the upper bounds of the tight inclusion functions to design two algorithms for the training and robustness verification of implicit neural networks. Finally, we apply our algorithms to train implicit neural networks on the MNIST dataset and compare the robustness of our models with the models trained via existing approaches in the literature.

Comparative Analysis of Interval Reachability for Robust Implicit and Feedforward Neural Networks

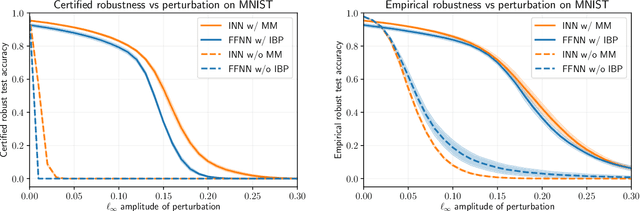
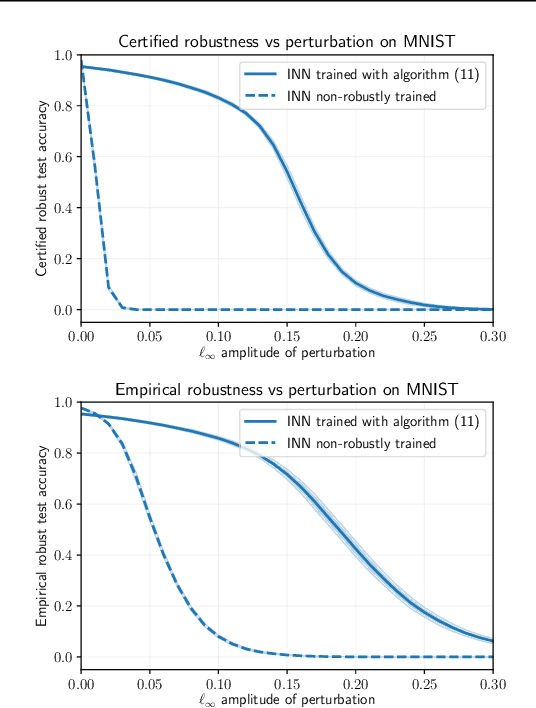
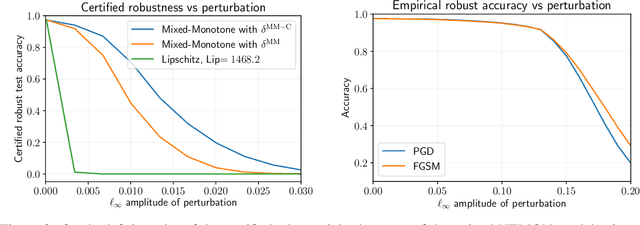
We use interval reachability analysis to obtain robustness guarantees for implicit neural networks (INNs). INNs are a class of implicit learning models that use implicit equations as layers and have been shown to exhibit several notable benefits over traditional deep neural networks. We first establish that tight inclusion functions of neural networks, which provide the tightest rectangular over-approximation of an input-output map, lead to sharper robustness guarantees than the well-studied robustness measures of local Lipschitz constants. Like Lipschitz constants, tight inclusions functions are computationally challenging to obtain, and we thus propose using mixed monotonicity and contraction theory to obtain computationally efficient estimates of tight inclusion functions for INNs. We show that our approach performs at least as well as, and generally better than, applying state-of-the-art interval bound propagation methods to INNs. We design a novel optimization problem for training robust INNs and we provide empirical evidence that suitably-trained INNs can be more robust than comparably-trained feedforward networks.

Robustness Certificates for Implicit Neural Networks: A Mixed Monotone Contractive Approach

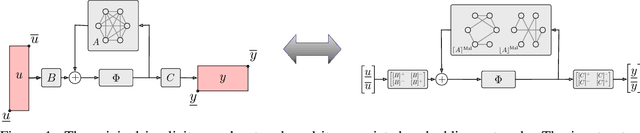
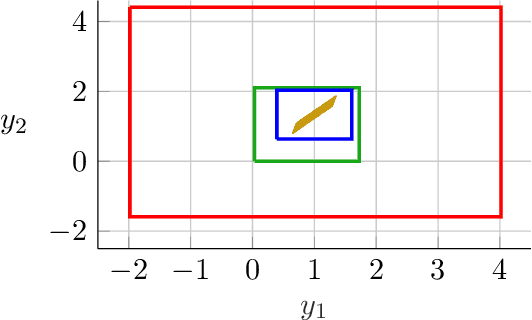
Implicit neural networks are a general class of learning models that replace the layers in traditional feedforward models with implicit algebraic equations. Compared to traditional learning models, implicit networks offer competitive performance and reduced memory consumption. However, they can remain brittle with respect to input adversarial perturbations. This paper proposes a theoretical and computational framework for robustness verification of implicit neural networks; our framework blends together mixed monotone systems theory and contraction theory. First, given an implicit neural network, we introduce a related embedded network and show that, given an $\ell_\infty$-norm box constraint on the input, the embedded network provides an $\ell_\infty$-norm box overapproximation for the output of the given network. Second, using $\ell_{\infty}$-matrix measures, we propose sufficient conditions for well-posedness of both the original and embedded system and design an iterative algorithm to compute the $\ell_{\infty}$-norm box robustness margins for reachability and classification problems. Third, of independent value, we propose a novel relative classifier variable that leads to tighter bounds on the certified adversarial robustness in classification problems. Finally, we perform numerical simulations on a Non-Euclidean Monotone Operator Network (NEMON) trained on the MNIST dataset. In these simulations, we compare the accuracy and run time of our mixed monotone contractive approach with the existing robustness verification approaches in the literature for estimating the certified adversarial robustness.

Robust Implicit Networks via Non-Euclidean Contractions

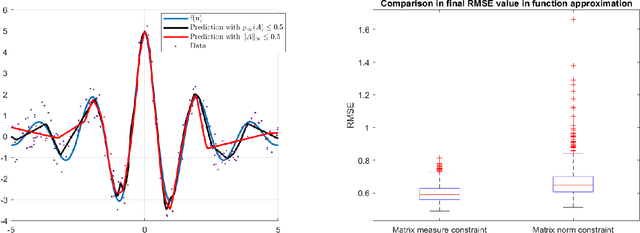
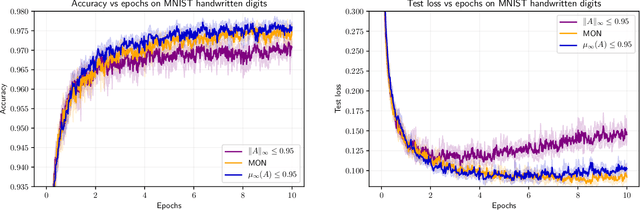
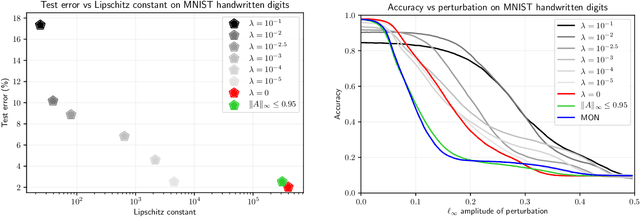
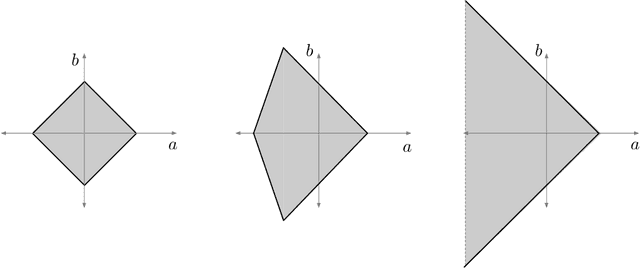
Implicit neural networks, a.k.a., deep equilibrium networks, are a class of implicit-depth learning models where function evaluation is performed by solving a fixed point equation. They generalize classic feedforward models and are equivalent to infinite-depth weight-tied feedforward networks. While implicit models show improved accuracy and significant reduction in memory consumption, they can suffer from ill-posedness and convergence instability. This paper provides a new framework to design well-posed and robust implicit neural networks based upon contraction theory for the non-Euclidean norm $\ell_\infty$. Our framework includes (i) a novel condition for well-posedness based on one-sided Lipschitz constants, (ii) an average iteration for computing fixed-points, and (iii) explicit estimates on input-output Lipschitz constants. Additionally, we design a training problem with the well-posedness condition and the average iteration as constraints and, to achieve robust models, with the input-output Lipschitz constant as a regularizer. Our $\ell_\infty$ well-posedness condition leads to a larger polytopic training search space than existing conditions and our average iteration enjoys accelerated convergence. Finally, we perform several numerical experiments for function estimation and digit classification through the MNIST data set. Our numerical results demonstrate improved accuracy and robustness of the implicit models with smaller input-output Lipschitz bounds.