A Nonlinear Separation Principle: Applications to Neural Networks, Control and Learning

This paper investigates continuous-time and discrete-time firing-rate and Hopfield recurrent neural networks (RNNs), with applications in nonlinear control design and implicit deep learning. First, we introduce a nonlinear separation principle that guarantees global exponential stability for the interconnection of a contracting state-feedback controller and a contracting observer, alongside parametric extensions for robustness and equilibrium tracking. Second, we derive sharp linear matrix inequality (LMI) conditions that guarantee the contractivity of both firing rate and Hopfield neural network architectures. We establish structural relationships among these certificates-demonstrating that continuous-time models with monotone non-decreasing activations maximize the admissible weight space, and extend these stability guarantees to interconnected systems and Graph RNNs. Third, we combine our separation principle and LMI framework to solve the output reference tracking problem for RNN-modeled plants. We provide LMI synthesis methods for feedback controllers and observers, and rigorously design a low-gain integral controller to eliminate steady-state error. Finally, we derive an exact, unconstrained algebraic parameterization of our contraction LMIs to design highly expressive implicit neural networks, achieving competitive accuracy and parameter efficiency on standard image classification benchmarks.

Proximal Gradient Dynamics: Monotonicity, Exponential Convergence, and Applications

In this letter, we study the proximal gradient dynamics. This recently-proposed continuous-time dynamics solves optimization problems whose cost functions are separable into a nonsmooth convex and a smooth component. First, we show that the cost function decreases monotonically along the trajectories of the proximal gradient dynamics. We then introduce a new condition that guarantees exponential convergence of the cost function to its optimal value, and show that this condition implies the proximal Polyak-{\L}ojasiewicz condition. We also show that the proximal Polyak-{\L}ojasiewicz condition guarantees exponential convergence of the cost function. Moreover, we extend these results to time-varying optimization problems, providing bounds for equilibrium tracking. Finally, we discuss applications of these findings, including the LASSO problem, quadratic optimization with polytopic constraints, and certain matrix based problems.

Contracting Dynamics for Time-Varying Convex Optimization

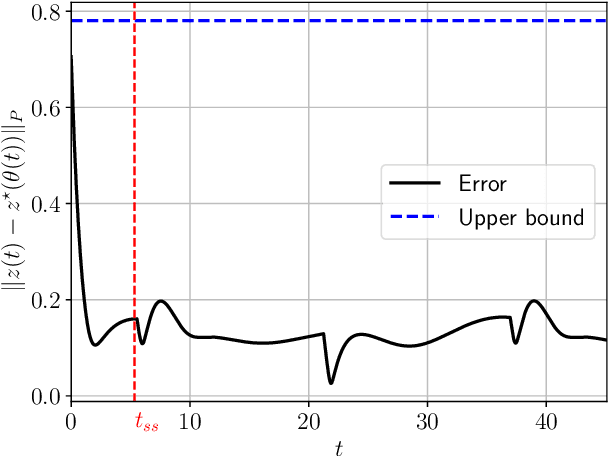
In this article, we provide a novel and broadly-applicable contraction-theoretic approach to continuous-time time-varying convex optimization. For any parameter-dependent contracting dynamics, we show that the tracking error between any solution trajectory and the equilibrium trajectory is uniformly upper bounded in terms of the contraction rate, the Lipschitz constant in which the parameter appears, and the rate of change of the parameter. To apply this result to time-varying convex optimization problems, we establish the strong infinitesimal contraction of dynamics solving three canonical problems, namely monotone inclusions, linear equality-constrained problems, and composite minimization problems. For each of these problems, we prove the sharpest-known rates of contraction and provide explicit tracking error bounds between solution trajectories and minimizing trajectories. We validate our theoretical results on two numerical examples.

Distributed Online Optimization with Byzantine Adversarial Agents

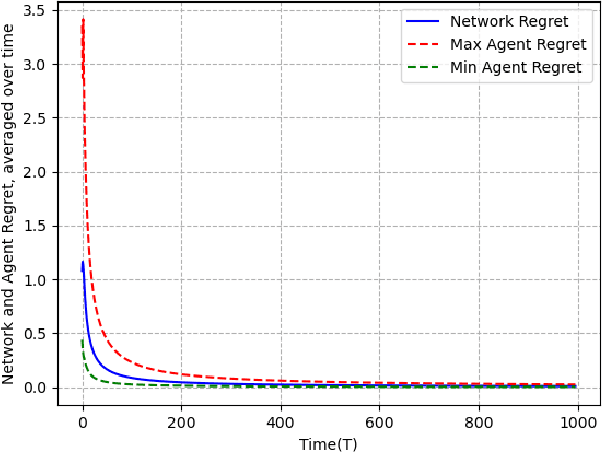
We study the problem of non-constrained, discrete-time, online distributed optimization in a multi-agent system where some of the agents do not follow the prescribed update rule either due to failures or malicious intentions. None of the agents have prior information about the identities of the faulty agents and any agent can communicate only with its immediate neighbours. At each time step, a Lipschitz strongly convex cost function is revealed locally to all the agents and the non-faulty agents update their states using their local information and the information obtained from their neighbours. We measure the performance of the online algorithm by comparing it to its offline version when the cost functions are known apriori. The difference between the same is termed as regret. Under sufficient conditions on the graph topology, the number and location of the adversaries, the defined regret grows sublinearly. We further conduct numerical experiments to validate our theoretical results.