Firing Rate Models as Associative Memory: Excitatory-Inhibitory Balance for Robust Retrieval

Firing rate models are dynamical systems widely used in applied and theoretical neuroscience to describe local cortical dynamics in neuronal populations. By providing a macroscopic perspective of neuronal activity, these models are essential for investigating oscillatory phenomena, chaotic behavior, and associative memory processes. Despite their widespread use, the application of firing rate models to associative memory networks has received limited mathematical exploration, and most existing studies are focused on specific models. Conversely, well-established associative memory designs, such as Hopfield networks, lack key biologically-relevant features intrinsic to firing rate models, including positivity and interpretable synaptic matrices that reflect excitatory and inhibitory interactions. To address this gap, we propose a general framework that ensures the emergence of re-scaled memory patterns as stable equilibria in the firing rate dynamics. Furthermore, we analyze the conditions under which the memories are locally and globally asymptotically stable, providing insights into constructing biologically-plausible and robust systems for associative memory retrieval.

Proximal Gradient Dynamics: Monotonicity, Exponential Convergence, and Applications

In this letter, we study the proximal gradient dynamics. This recently-proposed continuous-time dynamics solves optimization problems whose cost functions are separable into a nonsmooth convex and a smooth component. First, we show that the cost function decreases monotonically along the trajectories of the proximal gradient dynamics. We then introduce a new condition that guarantees exponential convergence of the cost function to its optimal value, and show that this condition implies the proximal Polyak-{\L}ojasiewicz condition. We also show that the proximal Polyak-{\L}ojasiewicz condition guarantees exponential convergence of the cost function. Moreover, we extend these results to time-varying optimization problems, providing bounds for equilibrium tracking. Finally, we discuss applications of these findings, including the LASSO problem, quadratic optimization with polytopic constraints, and certain matrix based problems.

Learning Neural Contracting Dynamics: Extended Linearization and Global Guarantees

Global stability and robustness guarantees in learned dynamical systems are essential to ensure well-behavedness of the systems in the face of uncertainty. We present Extended Linearized Contracting Dynamics (ELCD), the first neural network-based dynamical system with global contractivity guarantees in arbitrary metrics. The key feature of ELCD is a parametrization of the extended linearization of the nonlinear vector field. In its most basic form, ELCD is guaranteed to be (i) globally exponentially stable, (ii) equilibrium contracting, and (iii) globally contracting with respect to some metric. To allow for contraction with respect to more general metrics in the data space, we train diffeomorphisms between the data space and a latent space and enforce contractivity in the latent space, which ensures global contractivity in the data space. We demonstrate the performance of ELCD on the $2$D, $4$D, and $8$D LASA datasets.

IDKM: Memory Efficient Neural Network Quantization via Implicit, Differentiable k-Means

Compressing large neural networks with minimal performance loss is crucial to enabling their deployment on edge devices. (Cho et al., 2022) proposed a weight quantization method that uses an attention-based clustering algorithm called differentiable $k$-means (DKM). Despite achieving state-of-the-art results, DKM's performance is constrained by its heavy memory dependency. We propose an implicit, differentiable $k$-means algorithm (IDKM), which eliminates the major memory restriction of DKM. Let $t$ be the number of $k$-means iterations, $m$ be the number of weight-vectors, and $b$ be the number of bits per cluster address. IDKM reduces the overall memory complexity of a single $k$-means layer from $\mathcal{O}(t \cdot m \cdot 2^b)$ to $\mathcal{O}( m \cdot 2^b)$. We also introduce a variant, IDKM with Jacobian-Free-Backpropagation (IDKM-JFB), for which the time complexity of the gradient calculation is independent of $t$ as well. We provide a proof of concept of our methods by showing that, under the same settings, IDKM achieves comparable performance to DKM with less compute time and less memory. We also use IDKM and IDKM-JFB to quantize a large neural network, Resnet18, on hardware where DKM cannot train at all.

Multiplayer Homicidal Chauffeur Reach-Avoid Games: A Pursuit Enclosure Function Approach

This paper presents a multiplayer Homicidal Chauffeur reach-avoid differential game, which involves Dubins-car pursuers and simple-motion evaders. The goal of the pursuers is to cooperatively protect a planar convex region from the evaders, who strive to reach the region. We propose a cooperative strategy for the pursuers based on subgames for multiple pursuers against one evader and optimal task allocation. We introduce pursuit enclosure functions (PEFs) and propose a new enclosure region pursuit (ERP) winning approach that supports forward analysis for the strategy synthesis in the subgames. We show that if a pursuit coalition is able to defend the region against an evader under the ERP winning, then no more than two pursuers in the coalition are necessarily needed. We also propose a steer-to-ERP approach to certify the ERP winning and synthesize the ERP winning strategy. To implement the strategy, we introduce a positional PEF and provide the necessary parameters, states, and strategies that ensure the ERP winning for both one pursuer and two pursuers against one evader. Additionally, we formulate a binary integer program using the subgame outcomes to maximize the captured evaders in the ERP winning for the pursuit task allocation. Finally, we propose a multiplayer receding-horizon strategy where the ERP winnings are checked in each horizon, the task is allocated, and the strategies of the pursuers are determined. Numerical examples are provided to illustrate the results.

RoSSO: A High-Performance Python Package for Robotic Surveillance Strategy Optimization Using JAX

To enable the computation of effective randomized patrol routes for single- or multi-robot teams, we present RoSSO, a Python package designed for solving Markov chain optimization problems. We exploit machine-learning techniques such as reverse-mode automatic differentiation and constraint parametrization to achieve superior efficiency compared to general-purpose nonlinear programming solvers. Additionally, we supplement a game-theoretic stochastic surveillance formulation in the literature with a novel greedy algorithm and multi-robot extension. We close with numerical results for a police district in downtown San Francisco that demonstrate RoSSO's capabilities on our new formulations and the prior work.

Contracting Dynamics for Time-Varying Convex Optimization

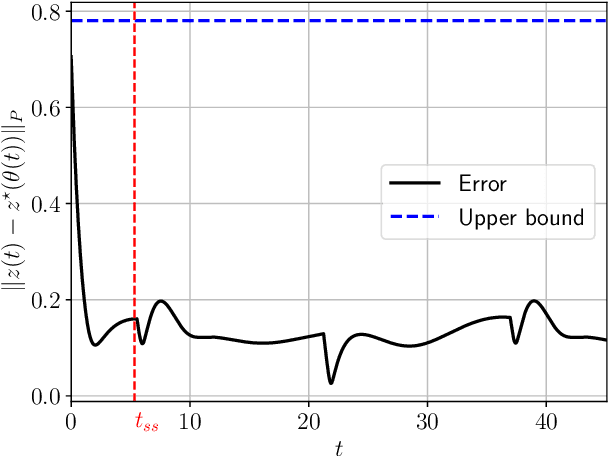
In this article, we provide a novel and broadly-applicable contraction-theoretic approach to continuous-time time-varying convex optimization. For any parameter-dependent contracting dynamics, we show that the tracking error between any solution trajectory and the equilibrium trajectory is uniformly upper bounded in terms of the contraction rate, the Lipschitz constant in which the parameter appears, and the rate of change of the parameter. To apply this result to time-varying convex optimization problems, we establish the strong infinitesimal contraction of dynamics solving three canonical problems, namely monotone inclusions, linear equality-constrained problems, and composite minimization problems. For each of these problems, we prove the sharpest-known rates of contraction and provide explicit tracking error bounds between solution trajectories and minimizing trajectories. We validate our theoretical results on two numerical examples.

Robust Training and Verification of Implicit Neural Networks: A Non-Euclidean Contractive Approach

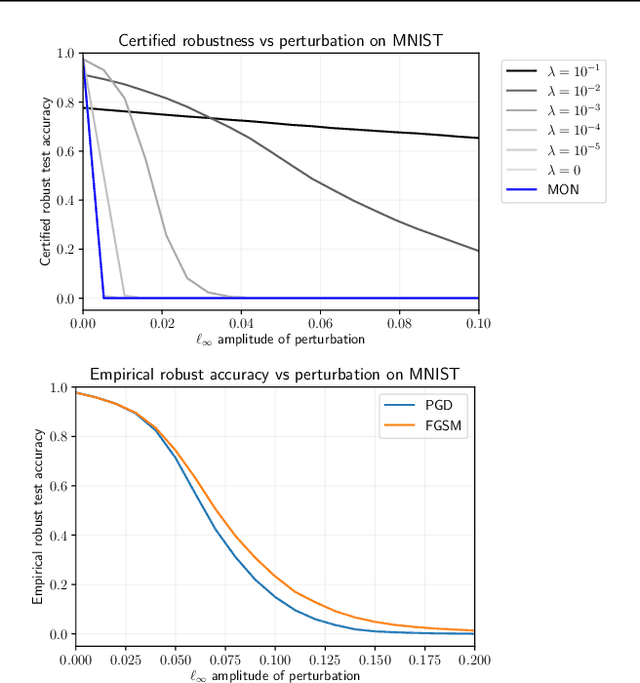
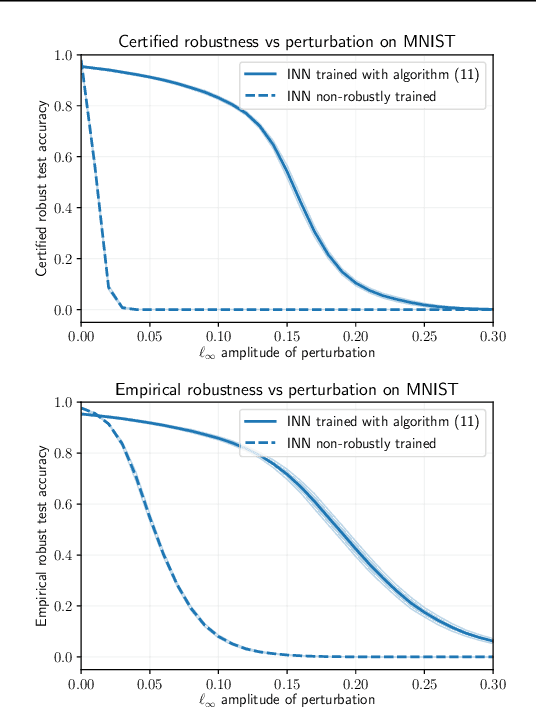
This paper proposes a theoretical and computational framework for training and robustness verification of implicit neural networks based upon non-Euclidean contraction theory. The basic idea is to cast the robustness analysis of a neural network as a reachability problem and use (i) the $\ell_{\infty}$-norm input-output Lipschitz constant and (ii) the tight inclusion function of the network to over-approximate its reachable sets. First, for a given implicit neural network, we use $\ell_{\infty}$-matrix measures to propose sufficient conditions for its well-posedness, design an iterative algorithm to compute its fixed points, and provide upper bounds for its $\ell_\infty$-norm input-output Lipschitz constant. Second, we introduce a related embedded network and show that the embedded network can be used to provide an $\ell_\infty$-norm box over-approximation of the reachable sets of the original network. Moreover, we use the embedded network to design an iterative algorithm for computing the upper bounds of the original system's tight inclusion function. Third, we use the upper bounds of the Lipschitz constants and the upper bounds of the tight inclusion functions to design two algorithms for the training and robustness verification of implicit neural networks. Finally, we apply our algorithms to train implicit neural networks on the MNIST dataset and compare the robustness of our models with the models trained via existing approaches in the literature.

Comparative Analysis of Interval Reachability for Robust Implicit and Feedforward Neural Networks

We use interval reachability analysis to obtain robustness guarantees for implicit neural networks (INNs). INNs are a class of implicit learning models that use implicit equations as layers and have been shown to exhibit several notable benefits over traditional deep neural networks. We first establish that tight inclusion functions of neural networks, which provide the tightest rectangular over-approximation of an input-output map, lead to sharper robustness guarantees than the well-studied robustness measures of local Lipschitz constants. Like Lipschitz constants, tight inclusions functions are computationally challenging to obtain, and we thus propose using mixed monotonicity and contraction theory to obtain computationally efficient estimates of tight inclusion functions for INNs. We show that our approach performs at least as well as, and generally better than, applying state-of-the-art interval bound propagation methods to INNs. We design a novel optimization problem for training robust INNs and we provide empirical evidence that suitably-trained INNs can be more robust than comparably-trained feedforward networks.

Modeling Human-AI Team Decision Making

AI and humans bring complementary skills to group deliberations. Modeling this group decision making is especially challenging when the deliberations include an element of risk and an exploration-exploitation process of appraising the capabilities of the human and AI agents. To investigate this question, we presented a sequence of intellective issues to a set of human groups aided by imperfect AI agents. A group's goal was to appraise the relative expertise of the group's members and its available AI agents, evaluate the risks associated with different actions, and maximize the overall reward by reaching consensus. We propose and empirically validate models of human-AI team decision making under such uncertain circumstances, and show the value of socio-cognitive constructs of prospect theory, influence dynamics, and Bayesian learning in predicting the behavior of human-AI groups.