Neural Network-assisted Interval Reachability for Systems with Control Barrier Function-Based Safe Controllers

Control Barrier Functions (CBFs) have been widely utilized in the design of optimization-based controllers and filters for dynamical systems to ensure forward invariance of a given set of safe states. While CBF-based controllers offer safety guarantees, they can compromise the performance of the system, leading to undesirable behaviors such as unbounded trajectories and emergence of locally stable spurious equilibria. Computing reachable sets for systems with CBF-based controllers is an effective approach for runtime performance and stability verification, and can potentially serve as a tool for trajectory re-planning. In this paper, we propose a computationally efficient interval reachability method for performance verification of systems with optimization-based controllers by: (i) approximating the optimization-based controller by a pre-trained neural network to avoid solving optimization problems repeatedly, and (ii) using mixed monotone theory to construct an embedding system that leverages state-of-the-art neural network verification algorithms for bounding the output of the neural network. Results in terms of closeness of solutions of trajectories of the system with the optimization-based controller and the neural network are derived. Using a single trajectory of the embedding system along with our closeness of solutions result, we obtain an over-approximation of the reachable set of the system with optimization-based controllers. Numerical results are presented to corroborate the technical findings.

$\texttt{immrax}$: A Parallelizable and Differentiable Toolbox for Interval Analysis and Mixed Monotone Reachability in JAX

We present an implementation of interval analysis and mixed monotone interval reachability analysis as function transforms in Python, fully composable with the computational framework JAX. The resulting toolbox inherits several key features from JAX, including computational efficiency through Just-In-Time Compilation, GPU acceleration for quick parallelized computations, and Automatic Differentiability. We demonstrate the toolbox's performance on several case studies, including a reachability problem on a vehicle model controlled by a neural network, and a robust closed-loop optimal control problem for a swinging pendulum.

Forward Invariance in Neural Network Controlled Systems

We present a framework based on interval analysis and monotone systems theory to certify and search for forward invariant sets in nonlinear systems with neural network controllers. The framework (i) constructs localized first-order inclusion functions for the closed-loop system using Jacobian bounds and existing neural network verification tools; (ii) builds a dynamical embedding system where its evaluation along a single trajectory directly corresponds with a nested family of hyper-rectangles provably converging to an attractive set of the original system; (iii) utilizes linear transformations to build families of nested paralleletopes with the same properties. The framework is automated in Python using our interval analysis toolbox $\texttt{npinterval}$, in conjunction with the symbolic arithmetic toolbox $\texttt{sympy}$, demonstrated on an $8$-dimensional leader-follower system.

Efficient Interaction-Aware Interval Analysis of Neural Network Feedback Loops

In this paper, we propose a computationally efficient framework for interval reachability of systems with neural network controllers. Our approach leverages inclusion functions for the open-loop system and the neural network controller to embed the closed-loop system into a larger-dimensional embedding system, where a single trajectory over-approximates the original system's behavior under uncertainty. We propose two methods for constructing closed-loop embedding systems, which account for the interactions between the system and the controller in different ways. The interconnection-based approach considers the worst-case evolution of each coordinate separately by substituting the neural network inclusion function into the open-loop inclusion function. The interaction-based approach uses novel Jacobian-based inclusion functions to capture the first-order interactions between the open-loop system and the controller by leveraging state-of-the-art neural network verifiers. Finally, we implement our approach in a Python framework called ReachMM to demonstrate its efficiency and scalability on benchmarks and examples ranging to $200$ state dimensions.

A Toolbox for Fast Interval Arithmetic in numpy with an Application to Formal Verification of Neural Network Controlled Systems

In this paper, we present a toolbox for interval analysis in numpy, with an application to formal verification of neural network controlled systems. Using the notion of natural inclusion functions, we systematically construct interval bounds for a general class of mappings. The toolbox offers efficient computation of natural inclusion functions using compiled C code, as well as a familiar interface in numpy with its canonical features, such as n-dimensional arrays, matrix/vector operations, and vectorization. We then use this toolbox in formal verification of dynamical systems with neural network controllers, through the composition of their inclusion functions.

Contraction-Guided Adaptive Partitioning for Reachability Analysis of Neural Network Controlled Systems

In this paper, we present a contraction-guided adaptive partitioning algorithm for improving interval-valued robust reachable set estimates in a nonlinear feedback loop with a neural network controller and disturbances. Based on an estimate of the contraction rate of over-approximated intervals, the algorithm chooses when and where to partition. Then, by leveraging a decoupling of the neural network verification step and reachability partitioning layers, the algorithm can provide accuracy improvements for little computational cost. This approach is applicable with any sufficiently accurate open-loop interval-valued reachability estimation technique and any method for bounding the input-output behavior of a neural network. Using contraction-based robustness analysis, we provide guarantees of the algorithm's performance with mixed monotone reachability. Finally, we demonstrate the algorithm's performance through several numerical simulations and compare it with existing methods in the literature. In particular, we report a sizable improvement in the accuracy of reachable set estimation in a fraction of the runtime as compared to state-of-the-art methods.

Interval Reachability of Nonlinear Dynamical Systems with Neural Network Controllers

This paper proposes a computationally efficient framework, based on interval analysis, for rigorous verification of nonlinear continuous-time dynamical systems with neural network controllers. Given a neural network, we use an existing verification algorithm to construct inclusion functions for its input-output behavior. Inspired by mixed monotone theory, we embed the closed-loop dynamics into a larger system using an inclusion function of the neural network and a decomposition function of the open-loop system. This embedding provides a scalable approach for safety analysis of the neural control loop while preserving the nonlinear structure of the system. We show that one can efficiently compute hyper-rectangular over-approximations of the reachable sets using a single trajectory of the embedding system. We design an algorithm to leverage this computational advantage through partitioning strategies, improving our reachable set estimates while balancing its runtime with tunable parameters. We demonstrate the performance of this algorithm through two case studies. First, we demonstrate this method's strength in complex nonlinear environments. Then, we show that our approach matches the performance of the state-of-the art verification algorithm for linear discretized systems.

Robust Training and Verification of Implicit Neural Networks: A Non-Euclidean Contractive Approach

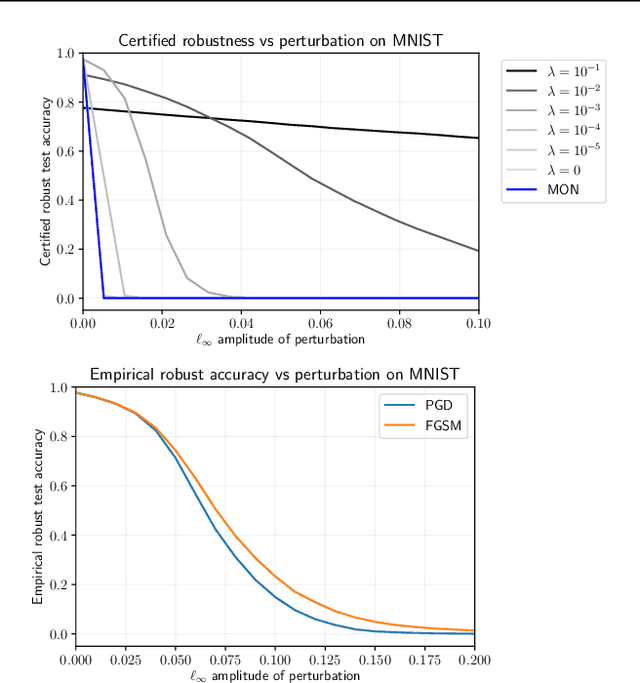
This paper proposes a theoretical and computational framework for training and robustness verification of implicit neural networks based upon non-Euclidean contraction theory. The basic idea is to cast the robustness analysis of a neural network as a reachability problem and use (i) the $\ell_{\infty}$-norm input-output Lipschitz constant and (ii) the tight inclusion function of the network to over-approximate its reachable sets. First, for a given implicit neural network, we use $\ell_{\infty}$-matrix measures to propose sufficient conditions for its well-posedness, design an iterative algorithm to compute its fixed points, and provide upper bounds for its $\ell_\infty$-norm input-output Lipschitz constant. Second, we introduce a related embedded network and show that the embedded network can be used to provide an $\ell_\infty$-norm box over-approximation of the reachable sets of the original network. Moreover, we use the embedded network to design an iterative algorithm for computing the upper bounds of the original system's tight inclusion function. Third, we use the upper bounds of the Lipschitz constants and the upper bounds of the tight inclusion functions to design two algorithms for the training and robustness verification of implicit neural networks. Finally, we apply our algorithms to train implicit neural networks on the MNIST dataset and compare the robustness of our models with the models trained via existing approaches in the literature.

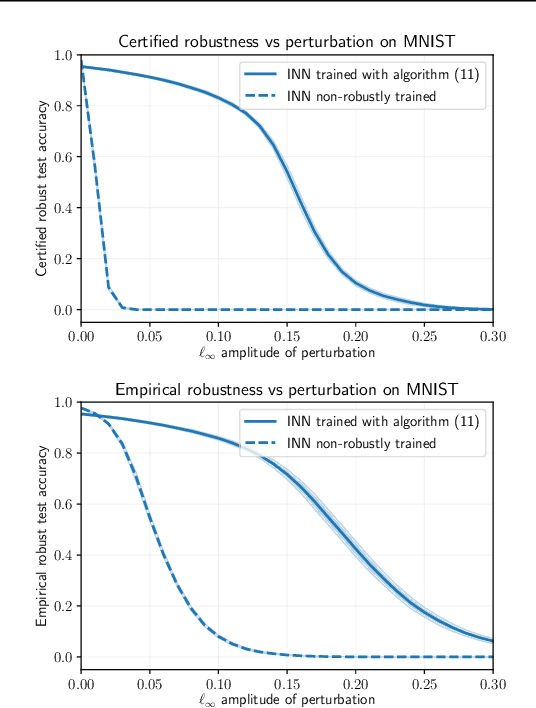
Comparative Analysis of Interval Reachability for Robust Implicit and Feedforward Neural Networks

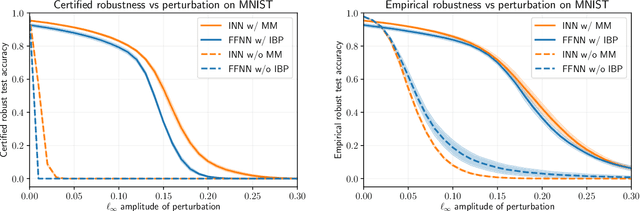
We use interval reachability analysis to obtain robustness guarantees for implicit neural networks (INNs). INNs are a class of implicit learning models that use implicit equations as layers and have been shown to exhibit several notable benefits over traditional deep neural networks. We first establish that tight inclusion functions of neural networks, which provide the tightest rectangular over-approximation of an input-output map, lead to sharper robustness guarantees than the well-studied robustness measures of local Lipschitz constants. Like Lipschitz constants, tight inclusions functions are computationally challenging to obtain, and we thus propose using mixed monotonicity and contraction theory to obtain computationally efficient estimates of tight inclusion functions for INNs. We show that our approach performs at least as well as, and generally better than, applying state-of-the-art interval bound propagation methods to INNs. We design a novel optimization problem for training robust INNs and we provide empirical evidence that suitably-trained INNs can be more robust than comparably-trained feedforward networks.

Robustness Certificates for Implicit Neural Networks: A Mixed Monotone Contractive Approach

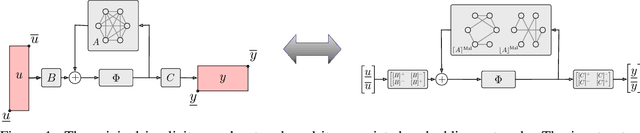
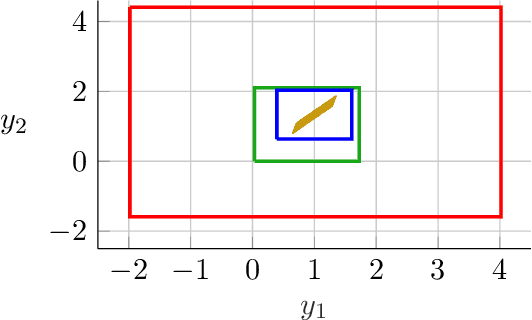
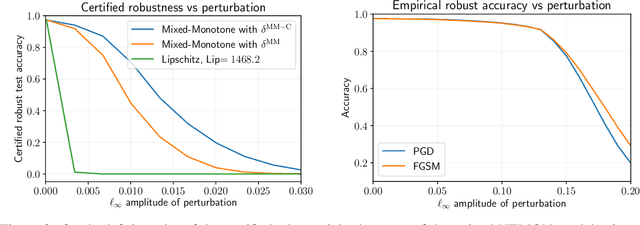
Implicit neural networks are a general class of learning models that replace the layers in traditional feedforward models with implicit algebraic equations. Compared to traditional learning models, implicit networks offer competitive performance and reduced memory consumption. However, they can remain brittle with respect to input adversarial perturbations. This paper proposes a theoretical and computational framework for robustness verification of implicit neural networks; our framework blends together mixed monotone systems theory and contraction theory. First, given an implicit neural network, we introduce a related embedded network and show that, given an $\ell_\infty$-norm box constraint on the input, the embedded network provides an $\ell_\infty$-norm box overapproximation for the output of the given network. Second, using $\ell_{\infty}$-matrix measures, we propose sufficient conditions for well-posedness of both the original and embedded system and design an iterative algorithm to compute the $\ell_{\infty}$-norm box robustness margins for reachability and classification problems. Third, of independent value, we propose a novel relative classifier variable that leads to tighter bounds on the certified adversarial robustness in classification problems. Finally, we perform numerical simulations on a Non-Euclidean Monotone Operator Network (NEMON) trained on the MNIST dataset. In these simulations, we compare the accuracy and run time of our mixed monotone contractive approach with the existing robustness verification approaches in the literature for estimating the certified adversarial robustness.