Certified Robust Invariant Polytope Training in Neural Controlled ODEs

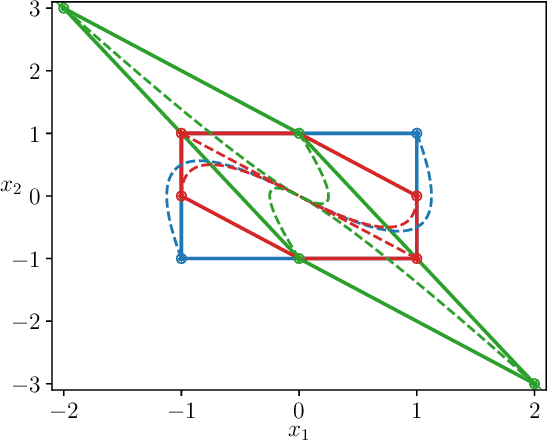
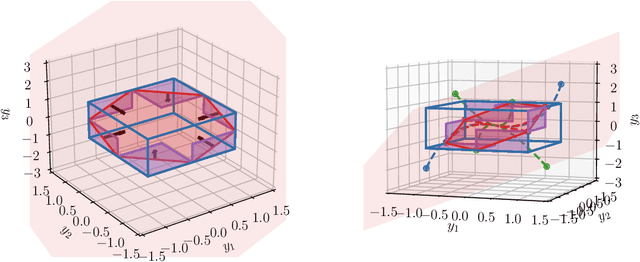
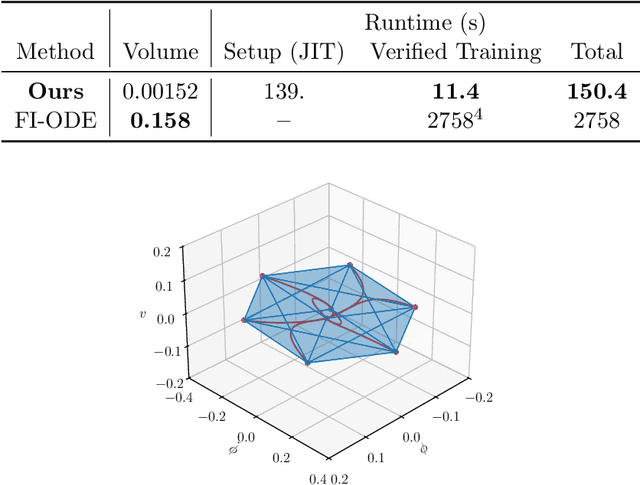
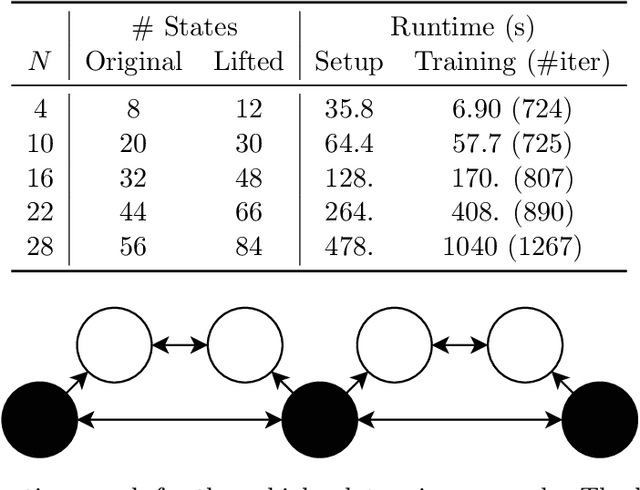
We consider a nonlinear control system modeled as an ordinary differential equation subject to disturbance, with a state feedback controller parameterized as a feedforward neural network. We propose a framework for training controllers with certified robust forward invariant polytopes, where any trajectory initialized inside the polytope remains within the polytope, regardless of the disturbance. First, we parameterize a family of lifted control systems in a higher dimensional space, where the original neural controlled system evolves on an invariant subspace of each lifted system. We use interval analysis and neural network verifiers to further construct a family of lifted embedding systems, carefully capturing the knowledge of this invariant subspace. If the vector field of any lifted embedding system satisfies a sign constraint at a single point, then a certain convex polytope of the original system is robustly forward invariant. Treating the neural network controller and the lifted system parameters as variables, we propose an algorithm to train controllers with certified forward invariant polytopes in the closed-loop control system. Through two examples, we demonstrate how the simplicity of the sign constraint allows our approach to scale with system dimension to over $50$ states, and outperform state-of-the-art Lyapunov-based sampling approaches in runtime.

$\texttt{immrax}$: A Parallelizable and Differentiable Toolbox for Interval Analysis and Mixed Monotone Reachability in JAX

We present an implementation of interval analysis and mixed monotone interval reachability analysis as function transforms in Python, fully composable with the computational framework JAX. The resulting toolbox inherits several key features from JAX, including computational efficiency through Just-In-Time Compilation, GPU acceleration for quick parallelized computations, and Automatic Differentiability. We demonstrate the toolbox's performance on several case studies, including a reachability problem on a vehicle model controlled by a neural network, and a robust closed-loop optimal control problem for a swinging pendulum.

Forward Invariance in Neural Network Controlled Systems

We present a framework based on interval analysis and monotone systems theory to certify and search for forward invariant sets in nonlinear systems with neural network controllers. The framework (i) constructs localized first-order inclusion functions for the closed-loop system using Jacobian bounds and existing neural network verification tools; (ii) builds a dynamical embedding system where its evaluation along a single trajectory directly corresponds with a nested family of hyper-rectangles provably converging to an attractive set of the original system; (iii) utilizes linear transformations to build families of nested paralleletopes with the same properties. The framework is automated in Python using our interval analysis toolbox $\texttt{npinterval}$, in conjunction with the symbolic arithmetic toolbox $\texttt{sympy}$, demonstrated on an $8$-dimensional leader-follower system.

Efficient Interaction-Aware Interval Analysis of Neural Network Feedback Loops

In this paper, we propose a computationally efficient framework for interval reachability of systems with neural network controllers. Our approach leverages inclusion functions for the open-loop system and the neural network controller to embed the closed-loop system into a larger-dimensional embedding system, where a single trajectory over-approximates the original system's behavior under uncertainty. We propose two methods for constructing closed-loop embedding systems, which account for the interactions between the system and the controller in different ways. The interconnection-based approach considers the worst-case evolution of each coordinate separately by substituting the neural network inclusion function into the open-loop inclusion function. The interaction-based approach uses novel Jacobian-based inclusion functions to capture the first-order interactions between the open-loop system and the controller by leveraging state-of-the-art neural network verifiers. Finally, we implement our approach in a Python framework called ReachMM to demonstrate its efficiency and scalability on benchmarks and examples ranging to $200$ state dimensions.

A Toolbox for Fast Interval Arithmetic in numpy with an Application to Formal Verification of Neural Network Controlled Systems

In this paper, we present a toolbox for interval analysis in numpy, with an application to formal verification of neural network controlled systems. Using the notion of natural inclusion functions, we systematically construct interval bounds for a general class of mappings. The toolbox offers efficient computation of natural inclusion functions using compiled C code, as well as a familiar interface in numpy with its canonical features, such as n-dimensional arrays, matrix/vector operations, and vectorization. We then use this toolbox in formal verification of dynamical systems with neural network controllers, through the composition of their inclusion functions.

Contraction-Guided Adaptive Partitioning for Reachability Analysis of Neural Network Controlled Systems

In this paper, we present a contraction-guided adaptive partitioning algorithm for improving interval-valued robust reachable set estimates in a nonlinear feedback loop with a neural network controller and disturbances. Based on an estimate of the contraction rate of over-approximated intervals, the algorithm chooses when and where to partition. Then, by leveraging a decoupling of the neural network verification step and reachability partitioning layers, the algorithm can provide accuracy improvements for little computational cost. This approach is applicable with any sufficiently accurate open-loop interval-valued reachability estimation technique and any method for bounding the input-output behavior of a neural network. Using contraction-based robustness analysis, we provide guarantees of the algorithm's performance with mixed monotone reachability. Finally, we demonstrate the algorithm's performance through several numerical simulations and compare it with existing methods in the literature. In particular, we report a sizable improvement in the accuracy of reachable set estimation in a fraction of the runtime as compared to state-of-the-art methods.

Interval Reachability of Nonlinear Dynamical Systems with Neural Network Controllers

This paper proposes a computationally efficient framework, based on interval analysis, for rigorous verification of nonlinear continuous-time dynamical systems with neural network controllers. Given a neural network, we use an existing verification algorithm to construct inclusion functions for its input-output behavior. Inspired by mixed monotone theory, we embed the closed-loop dynamics into a larger system using an inclusion function of the neural network and a decomposition function of the open-loop system. This embedding provides a scalable approach for safety analysis of the neural control loop while preserving the nonlinear structure of the system. We show that one can efficiently compute hyper-rectangular over-approximations of the reachable sets using a single trajectory of the embedding system. We design an algorithm to leverage this computational advantage through partitioning strategies, improving our reachable set estimates while balancing its runtime with tunable parameters. We demonstrate the performance of this algorithm through two case studies. First, we demonstrate this method's strength in complex nonlinear environments. Then, we show that our approach matches the performance of the state-of-the art verification algorithm for linear discretized systems.