Lightweight Tracking Control for Computationally Constrained Aerial Systems with the Newton-Raphson Method

We investigate the performance of a lightweight tracking controller, based on a flow version of the Newton-Raphson method, applied to a miniature blimp and a mid-size quadrotor. This tracking technique has been shown to enjoy theoretical guarantees of performance and has been applied with success in simulation studies and on mobile robots with simple motion models. This paper investigates the technique through real-world flight experiments on aerial hardware platforms subject to realistic deployment and onboard computational constraints. The technique's performance is assessed in comparison with the established control frameworks of feedback linearization for the blimp, and nonlinear model predictive control for both quadrotor and blimp. The performance metrics under consideration are (i) root mean square error of flight trajectories with respect to target trajectories, (ii) algorithms' computation times, and (iii) CPU energy consumption associated with the control algorithms. The experimental findings show that the Newton-Raphson flow-based tracking controller achieves comparable or superior tracking performance to the baseline methods with substantially reduced computation time and energy expenditure.

Seeing, Saying, Solving: An LLM-to-TL Framework for Cooperative Robots

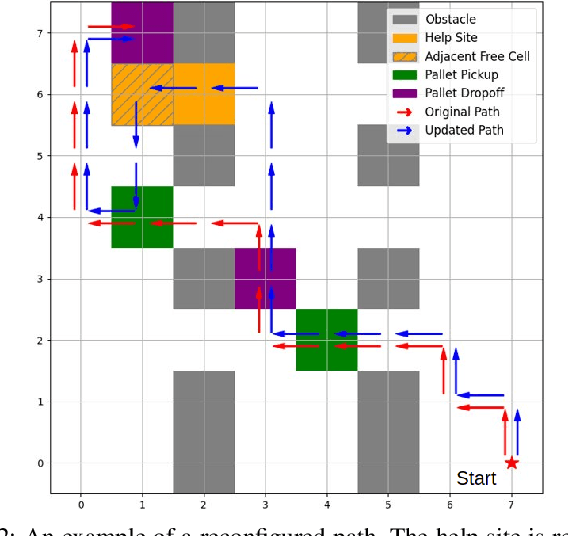
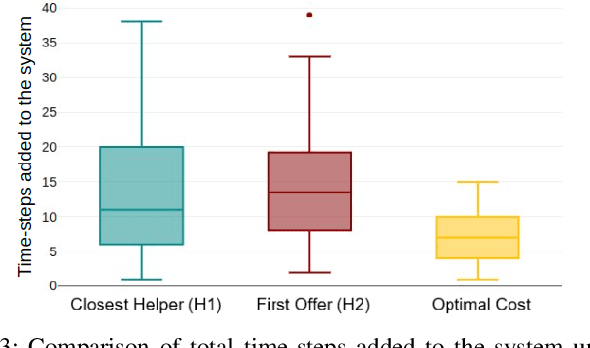
Increased robot deployment, such as in warehousing, has revealed a need for seamless collaboration among heterogeneous robot teams to resolve unforeseen conflicts. To address this challenge, we propose a novel, decentralized framework for robots to request and provide help. The framework begins with robots detecting conflicts using a Vision Language Model (VLM), then reasoning over whether help is needed. If so, it crafts and broadcasts a natural language (NL) help request using a Large Language Model (LLM). Potential helper robots reason over the request and offer help (if able), along with information about impact to their current tasks. Helper reasoning is implemented via an LLM grounded in Signal Temporal Logic (STL) using a Backus-Naur Form (BNF) grammar to guarantee syntactically valid NL-to-STL translations, which are then solved as a Mixed Integer Linear Program (MILP). Finally, the requester robot chooses a helper by reasoning over impact on the overall system. We evaluate our system via experiments considering different strategies for choosing a helper, and find that a requester robot can minimize overall time impact on the system by considering multiple help offers versus simple heuristics (e.g., selecting the nearest robot to help).

Optimization-based Task and Motion Planning under Signal Temporal Logic Specifications using Logic Network Flow

This paper proposes an optimization-based task and motion planning framework, named ``Logic Network Flow", to integrate signal temporal logic (STL) specifications into efficient mixed-binary linear programmings. In this framework, temporal predicates are encoded as polyhedron constraints on each edge of the network flow, instead of as constraints between the nodes as in the traditional Logic Tree formulation. Synthesized with Dynamic Network Flows, Logic Network Flows render a tighter convex relaxation compared to Logic Trees derived from these STL specifications. Our formulation is evaluated on several multi-robot motion planning case studies. Empirical results demonstrate that our formulation outperforms Logic Tree formulation in terms of computation time for several planning problems. As the problem size scales up, our method still discovers better lower and upper bounds by exploring fewer number of nodes during the branch-and-bound process, although this comes at the cost of increased computational load for each node when exploring branches.

Disturbance-Robust Backup Control Barrier Functions: Safety Under Uncertain Dynamics

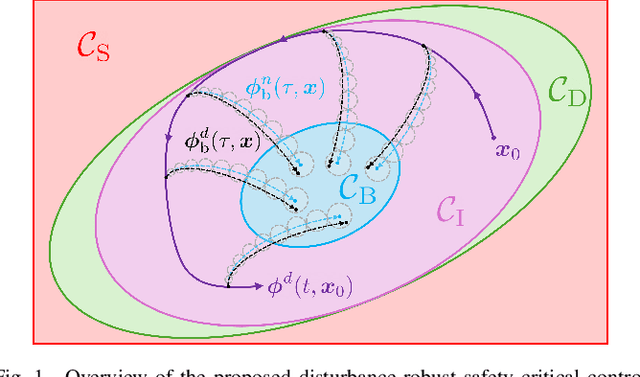
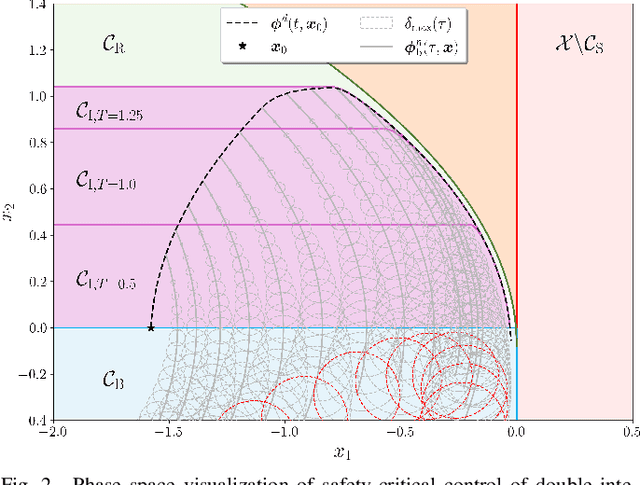
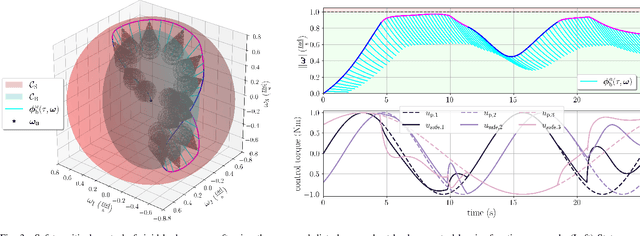
Obtaining a controlled invariant set is crucial for safety-critical control with control barrier functions (CBFs) but is non-trivial for complex nonlinear systems and constraints. Backup control barrier functions allow such sets to be constructed online in a computationally tractable manner by examining the evolution (or flow) of the system under a known backup control law. However, for systems with unmodeled disturbances, this flow cannot be directly computed, making the current methods inadequate for assuring safety in these scenarios. To address this gap, we leverage bounds on the nominal and disturbed flow to compute a forward invariant set online by ensuring safety of an expanding norm ball tube centered around the nominal system evolution. We prove that this set results in robust control constraints which guarantee safety of the disturbed system via our Disturbance-Robust Backup Control Barrier Function (DR-BCBF) solution. Additionally, the efficacy of the proposed framework is demonstrated in simulation, applied to a double integrator problem and a rigid body spacecraft rotation problem with rate constraints.

Newton-Raphson Flow for Aggressive Quadrotor Tracking Control

We apply the Newton-Raphson flow tracking controller to aggressive quadrotor flight and demonstrate that it achieves good tracking performance over a suite of benchmark trajectories, beating the native trajectory tracking controller in the popular PX4 Autopilot. The Newton-Raphson flow tracking controller is a recently proposed integrator-type controller that aims to drive to zero the error between a future predicted system output and the reference trajectory. This controller is computationally lightweight, requiring only an imprecise predictor, and achieves guaranteed asymptotic error bounds under certain conditions. We show that these theoretical advantages are realizable on a quadrotor hardware platform. Our experiments are conducted on a Holybrox x500v2 quadrotor using a Pixhawk 6x flight controller and a Rasbperry Pi 4 companion computer which receives location information from an OptiTrack motion capture system and sends input commands through the ROS2 API for the PX4 software stack.

Certified Robust Invariant Polytope Training in Neural Controlled ODEs

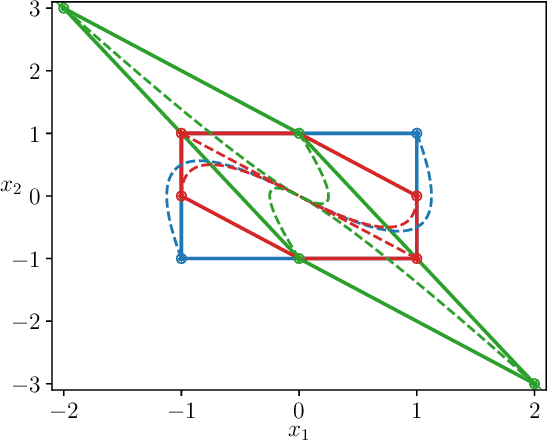
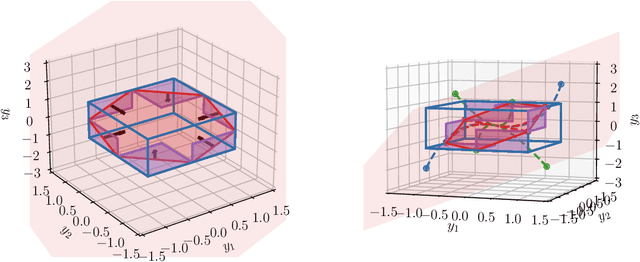
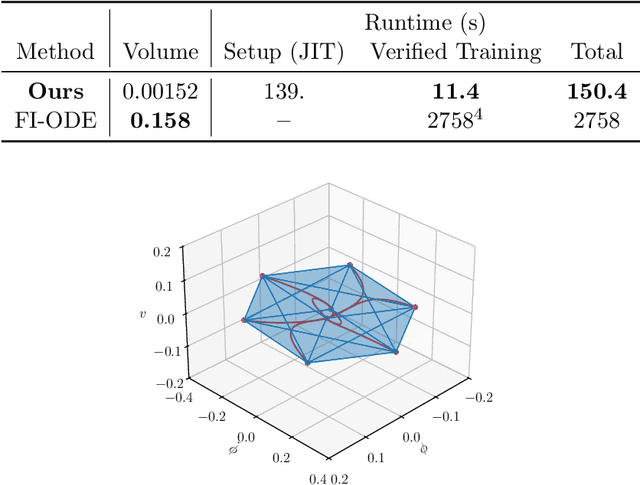
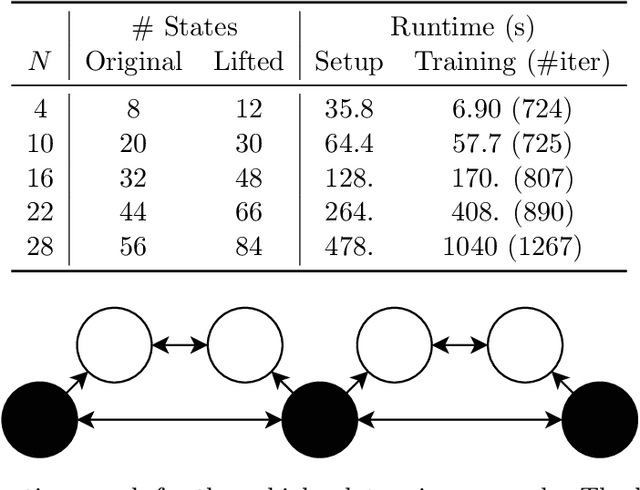
We consider a nonlinear control system modeled as an ordinary differential equation subject to disturbance, with a state feedback controller parameterized as a feedforward neural network. We propose a framework for training controllers with certified robust forward invariant polytopes, where any trajectory initialized inside the polytope remains within the polytope, regardless of the disturbance. First, we parameterize a family of lifted control systems in a higher dimensional space, where the original neural controlled system evolves on an invariant subspace of each lifted system. We use interval analysis and neural network verifiers to further construct a family of lifted embedding systems, carefully capturing the knowledge of this invariant subspace. If the vector field of any lifted embedding system satisfies a sign constraint at a single point, then a certain convex polytope of the original system is robustly forward invariant. Treating the neural network controller and the lifted system parameters as variables, we propose an algorithm to train controllers with certified forward invariant polytopes in the closed-loop control system. Through two examples, we demonstrate how the simplicity of the sign constraint allows our approach to scale with system dimension to over $50$ states, and outperform state-of-the-art Lyapunov-based sampling approaches in runtime.

A Unified Approach to Multi-task Legged Navigation: Temporal Logic Meets Reinforcement Learning

This study examines the problem of hopping robot navigation planning to achieve simultaneous goal-directed and environment exploration tasks. We consider a scenario in which the robot has mandatory goal-directed tasks defined using Linear Temporal Logic (LTL) specifications as well as optional exploration tasks represented using a reward function. Additionally, there exists uncertainty in the robot dynamics which results in motion perturbation. We first propose an abstraction of 3D hopping robot dynamics which enables high-level planning and a neural-network-based optimization for low-level control. We then introduce a Multi-task Product IMDP (MT-PIMDP) model of the system and tasks. We propose a unified control policy synthesis algorithm which enables both task-directed goal-reaching behaviors as well as task-agnostic exploration to learn perturbations and reward. We provide a formal proof of the trade-off induced by prioritizing either LTL or RL actions. We demonstrate our methods with simulation case studies in a 2D world navigation environment.

LTL-D*: Incrementally Optimal Replanning for Feasible and Infeasible Tasks in Linear Temporal Logic Specifications

This paper presents an incremental replanning algorithm, dubbed LTL-D*, for temporal-logic-based task planning in a dynamically changing environment. Unexpected changes in the environment may lead to failures in satisfying a task specification in the form of a Linear Temporal Logic (LTL). In this study, the considered failures are categorized into two classes: (i) the desired LTL specification can be satisfied via replanning, and (ii) the desired LTL specification is infeasible to meet strictly and can only be satisfied in a "relaxed" fashion. To address these failures, the proposed algorithm finds an optimal replanning solution that minimally violates desired task specifications. In particular, our approach leverages the D* Lite algorithm and employs a distance metric within the synthesized automaton to quantify the degree of the task violation and then replan incrementally. This ensures plan optimality and reduces planning time, especially when frequent replanning is required. Our approach is implemented in a robot navigation simulation to demonstrate a significant improvement in the computational efficiency for replanning by two orders of magnitude.

Bipedal Safe Navigation over Uncertain Rough Terrain: Unifying Terrain Mapping and Locomotion Stability

We study the problem of bipedal robot navigation in complex environments with uncertain and rough terrain. In particular, we consider a scenario in which the robot is expected to reach a desired goal location by traversing an environment with uncertain terrain elevation. Such terrain uncertainties induce not only untraversable regions but also robot motion perturbations. Thus, the problems of terrain mapping and locomotion stability are intertwined. We evaluate three different kernels for Gaussian process (GP) regression to learn the terrain elevation. We also learn the motion deviation resulting from both the terrain as well as the discrepancy between the reduced-order Prismatic Inverted Pendulum Model used for planning and the full-order locomotion dynamics. We propose a hierarchical locomotion-dynamics-aware sampling-based navigation planner. The global navigation planner plans a series of local waypoints to reach the desired goal locations while respecting locomotion stability constraints. Then, a local navigation planner is used to generate a sequence of dynamically feasible footsteps to reach local waypoints. We develop a novel trajectory evaluation metric to minimize motion deviation and maximize information gain of the terrain elevation map. We evaluate the efficacy of our planning framework on Digit bipedal robot simulation in MuJoCo.

$\texttt{immrax}$: A Parallelizable and Differentiable Toolbox for Interval Analysis and Mixed Monotone Reachability in JAX

We present an implementation of interval analysis and mixed monotone interval reachability analysis as function transforms in Python, fully composable with the computational framework JAX. The resulting toolbox inherits several key features from JAX, including computational efficiency through Just-In-Time Compilation, GPU acceleration for quick parallelized computations, and Automatic Differentiability. We demonstrate the toolbox's performance on several case studies, including a reachability problem on a vehicle model controlled by a neural network, and a robust closed-loop optimal control problem for a swinging pendulum.