Active Constraint Learning in High Dimensions from Demonstrations

We present an iterative active constraint learning (ACL) algorithm, within the learning from demonstrations (LfD) paradigm, which intelligently solicits informative demonstration trajectories for inferring an unknown constraint in the demonstrator's environment. Our approach iteratively trains a Gaussian process (GP) on the available demonstration dataset to represent the unknown constraints, uses the resulting GP posterior to query start/goal states, and generates informative demonstrations which are added to the dataset. Across simulation and hardware experiments using high-dimensional nonlinear dynamics and unknown nonlinear constraints, our method outperforms a baseline, random-sampling based method at accurately performing constraint inference from an iteratively generated set of sparse but informative demonstrations.

Language Conditioning Improves Accuracy of Aircraft Goal Prediction in Untowered Airspace

Autonomous aircraft must safely operate in untowered airspace, where coordination relies on voice-based communication among human pilots. Safe operation requires an aircraft to predict the intent, and corresponding goal location, of other aircraft. This paper introduces a multimodal framework for aircraft goal prediction that integrates natural language understanding with spatial reasoning to improve autonomous decision-making in such environments. We leverage automatic speech recognition and large language models to transcribe and interpret pilot radio calls, identify aircraft, and extract discrete intent labels. These intent labels are fused with observed trajectories to condition a temporal convolutional network and Gaussian mixture model for probabilistic goal prediction. Our method significantly reduces goal prediction error compared to baselines that rely solely on motion history, demonstrating that language-conditioned prediction increases prediction accuracy. Experiments on a real-world dataset from an untowered airport validate the approach and highlight its potential to enable socially aware, language-conditioned robotic motion planning.

Constraint Learning in Multi-Agent Dynamic Games from Demonstrations of Local Nash Interactions

We present an inverse dynamic game-based algorithm to learn parametric constraints from a given dataset of local generalized Nash equilibrium interactions between multiple agents. Specifically, we introduce mixed-integer linear programs (MILP) encoding the Karush-Kuhn-Tucker (KKT) conditions of the interacting agents, which recover constraints consistent with the Nash stationarity of the interaction demonstrations. We establish theoretical guarantees that our method learns inner approximations of the true safe and unsafe sets, as well as limitations of constraint learnability from demonstrations of Nash equilibrium interactions. We also use the interaction constraints recovered by our method to design motion plans that robustly satisfy the underlying constraints. Across simulations and hardware experiments, our methods proved capable of inferring constraints and designing interactive motion plans for various classes of constraints, both convex and non-convex, from interaction demonstrations of agents with nonlinear dynamics.

Seeing, Saying, Solving: An LLM-to-TL Framework for Cooperative Robots

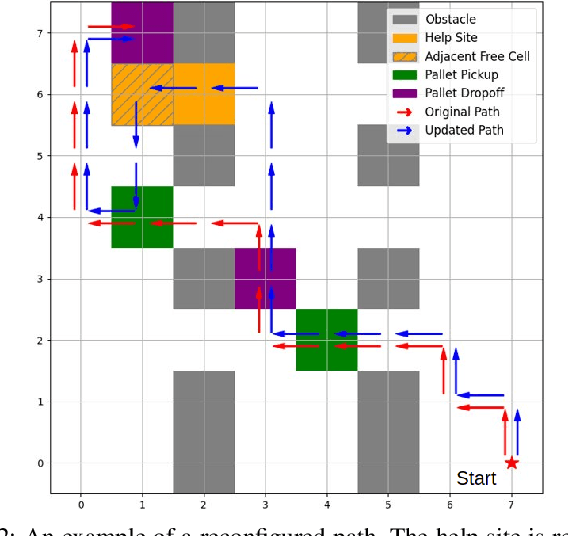
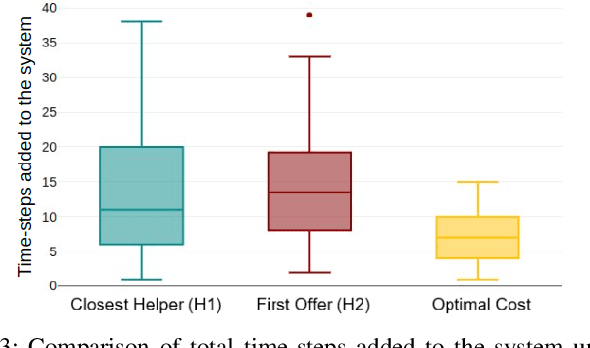
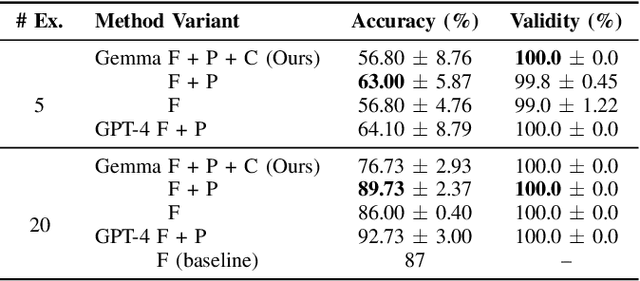
Increased robot deployment, such as in warehousing, has revealed a need for seamless collaboration among heterogeneous robot teams to resolve unforeseen conflicts. To address this challenge, we propose a novel, decentralized framework for robots to request and provide help. The framework begins with robots detecting conflicts using a Vision Language Model (VLM), then reasoning over whether help is needed. If so, it crafts and broadcasts a natural language (NL) help request using a Large Language Model (LLM). Potential helper robots reason over the request and offer help (if able), along with information about impact to their current tasks. Helper reasoning is implemented via an LLM grounded in Signal Temporal Logic (STL) using a Backus-Naur Form (BNF) grammar to guarantee syntactically valid NL-to-STL translations, which are then solved as a Mixed Integer Linear Program (MILP). Finally, the requester robot chooses a helper by reasoning over impact on the overall system. We evaluate our system via experiments considering different strategies for choosing a helper, and find that a requester robot can minimize overall time impact on the system by considering multiple help offers versus simple heuristics (e.g., selecting the nearest robot to help).

Contingency Games for Multi-Agent Interaction

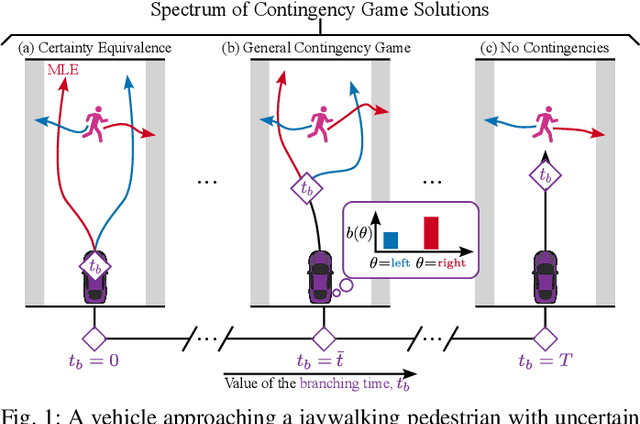
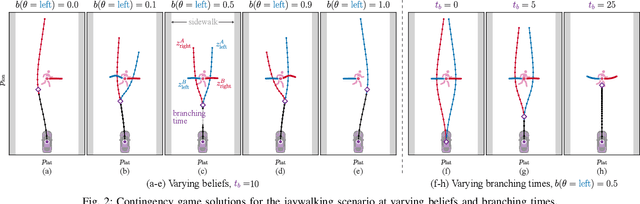
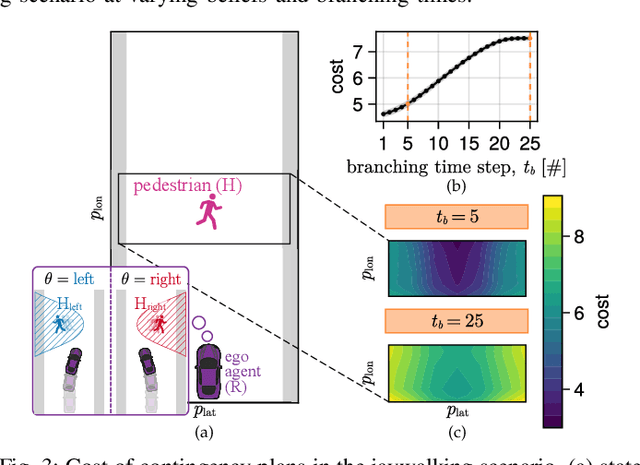
Contingency planning, wherein an agent generates a set of possible plans conditioned on the outcome of an uncertain event, is an increasingly popular way for robots to act under uncertainty. In this work, we take a game-theoretic perspective on contingency planning which is tailored to multi-agent scenarios in which a robot's actions impact the decisions of other agents and vice versa. The resulting contingency game allows the robot to efficiently coordinate with other agents by generating strategic motion plans conditioned on multiple possible intents for other actors in the scene. Contingency games are parameterized via a scalar variable which represents a future time at which intent uncertainty will be resolved. Varying this parameter enables a designer to easily adjust how conservatively the robot behaves in the game. Interestingly, we also find that existing variants of game-theoretic planning under uncertainty are readily obtained as special cases of contingency games. Lastly, we offer an efficient method for solving N-player contingency games with nonlinear dynamics and non-convex costs and constraints. Through a series of simulated autonomous driving scenarios, we demonstrate that plans generated via contingency games provide quantitative performance gains over game-theoretic motion plans that do not account for future uncertainty reduction.

Cost Inference for Feedback Dynamic Games from Noisy Partial State Observations and Incomplete Trajectories

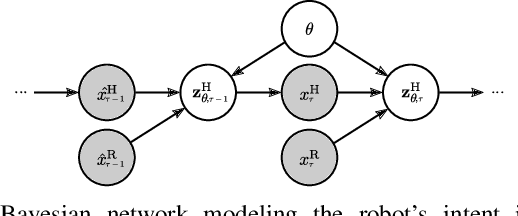
In multi-agent dynamic games, the Nash equilibrium state trajectory of each agent is determined by its cost function and the information pattern of the game. However, the cost and trajectory of each agent may be unavailable to the other agents. Prior work on using partial observations to infer the costs in dynamic games assumes an open-loop information pattern. In this work, we demonstrate that the feedback Nash equilibrium concept is more expressive and encodes more complex behavior. It is desirable to develop specific tools for inferring players' objectives in feedback games. Therefore, we consider the dynamic game cost inference problem under the feedback information pattern, using only partial state observations and incomplete trajectory data. To this end, we first propose an inverse feedback game loss function, whose minimizer yields a feedback Nash equilibrium state trajectory closest to the observation data. We characterize the landscape and differentiability of the loss function. Given the difficulty of obtaining the exact gradient, our main contribution is an efficient gradient approximator, which enables a novel inverse feedback game solver that minimizes the loss using first-order optimization. In thorough empirical evaluations, we demonstrate that our algorithm converges reliably and has better robustness and generalization performance than the open-loop baseline method when the observation data reflects a group of players acting in a feedback Nash game.

Towards Dynamic Causal Discovery with Rare Events: A Nonparametric Conditional Independence Test

Causal phenomena associated with rare events occur across a wide range of engineering problems, such as risk-sensitive safety analysis, accident analysis and prevention, and extreme value theory. However, current methods for causal discovery are often unable to uncover causal links, between random variables in a dynamic setting, that manifest only when the variables first experience low-probability realizations. To address this issue, we introduce a novel statistical independence test on data collected from time-invariant dynamical systems in which rare but consequential events occur. In particular, we exploit the time-invariance of the underlying data to construct a superimposed dataset of the system state before rare events happen at different timesteps. We then design a conditional independence test on the reorganized data. We provide non-asymptotic sample complexity bounds for the consistency of our method, and validate its performance across various simulated and real-world datasets, including incident data collected from the Caltrans Performance Measurement System (PeMS). Code containing the datasets and experiments is publicly available.

SLAM Backends with Objects in Motion: A Unifying Framework and Tutorial

Simultaneous Localization and Mapping (SLAM) algorithms are frequently deployed to support a wide range of robotics applications, such as autonomous navigation in unknown environments, and scene mapping in virtual reality. Many of these applications require autonomous agents to perform SLAM in highly dynamic scenes. To this end, this tutorial extends a recently introduced, unifying optimization-based SLAM backend framework to environments with moving objects and features. Using this framework, we consider a rapprochement of recent advances in dynamic SLAM. Moreover, we present dynamic EKF SLAM: a novel, filtering-based dynamic SLAM algorithm generated from our framework, and prove that it is mathematically equivalent to a direct extension of the classical EKF SLAM algorithm to the dynamic environment setting. Empirical results with simulated data indicate that dynamic EKF SLAM can achieve high localization and mobile object pose estimation accuracy, as well as high map precision, with high efficiency.

Pursuit of a Discriminative Representation for Multiple Subspaces via Sequential Games

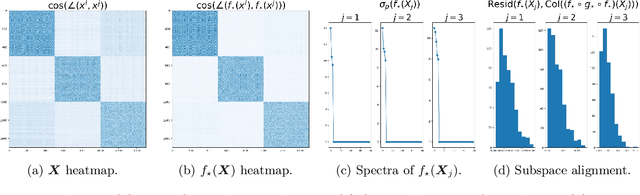
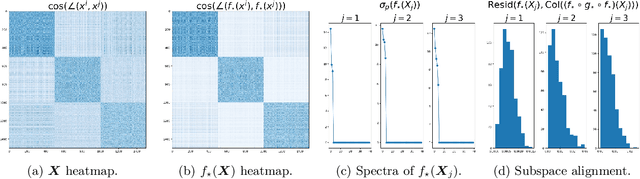
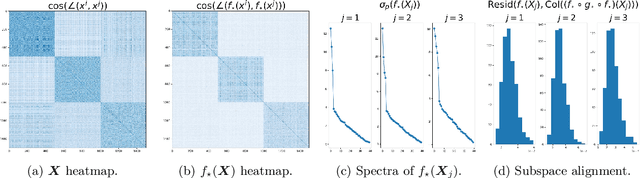
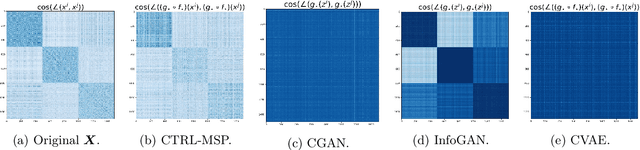
We consider the problem of learning discriminative representations for data in a high-dimensional space with distribution supported on or around multiple low-dimensional linear subspaces. That is, we wish to compute a linear injective map of the data such that the features lie on multiple orthogonal subspaces. Instead of treating this learning problem using multiple PCAs, we cast it as a sequential game using the closed-loop transcription (CTRL) framework recently proposed for learning discriminative and generative representations for general low-dimensional submanifolds. We prove that the equilibrium solutions to the game indeed give correct representations. Our approach unifies classical methods of learning subspaces with modern deep learning practice, by showing that subspace learning problems may be provably solved using the modern toolkit of representation learning. In addition, our work provides the first theoretical justification for the CTRL framework, in the important case of linear subspaces. We support our theoretical findings with compelling empirical evidence. We also generalize the sequential game formulation to more general representation learning problems. Our code, including methods for easy reproduction of experimental results, is publically available on GitHub.

GTP-SLAM: Game-Theoretic Priors for Simultaneous Localization and Mapping in Multi-Agent Scenarios

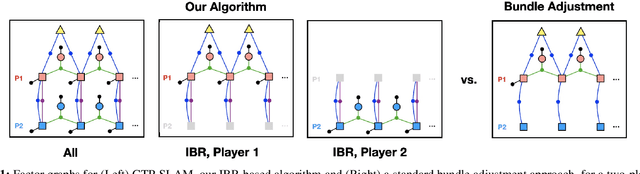
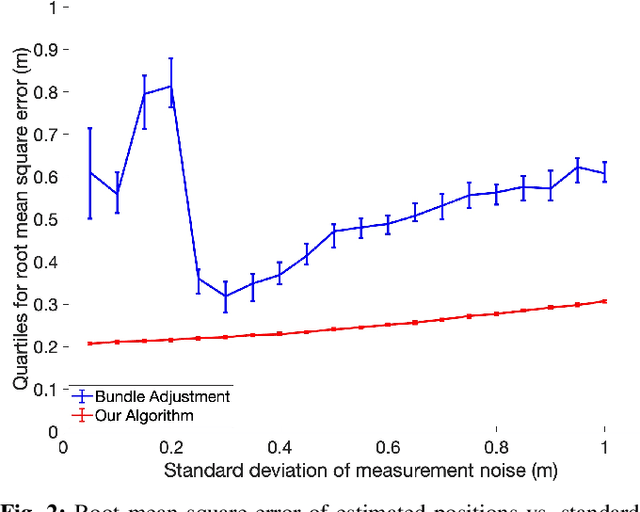
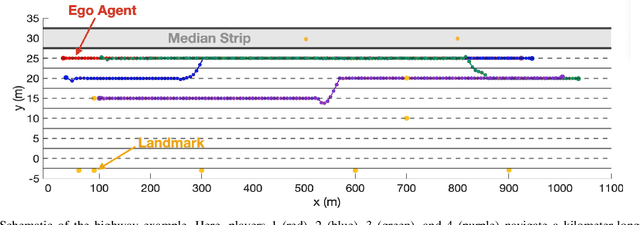
Robots operating in complex, multi-player settings must simultaneously model the environment and the behavior of human or robotic agents who share that environment. Environmental modeling is often approached using Simultaneous Localization and Mapping (SLAM) techniques; however, SLAM algorithms usually neglect multi-player interactions. In contrast, a recent branch of the motion planning literature uses dynamic game theory to explicitly model noncooperative interactions of multiple agents in a known environment with perfect localization. In this work, we fuse ideas from these disparate communities to solve SLAM problems with game theoretic priors. We present GTP-SLAM, a novel, iterative best response-based SLAM algorithm that accurately performs state localization and map reconstruction in an uncharted scene, while capturing the inherent game-theoretic interactions among multiple agents in that scene. By formulating the underlying SLAM problem as a potential game, we inherit a strong convergence guarantee. Empirical results indicate that, when deployed in a realistic traffic simulation, our approach performs localization and mapping more accurately than a standard bundle adjustment algorithm across a wide range of noise levels.