Parallel Stochastic Gradient-Based Planning for World Models

World models simulate environment dynamics from raw sensory inputs like video. However, using them for planning can be challenging due to the vast and unstructured search space. We propose a robust and highly parallelizable planner that leverages the differentiability of the learned world model for efficient optimization, solving long-horizon control tasks from visual input. Our method treats states as optimization variables ("virtual states") with soft dynamics constraints, enabling parallel computation and easier optimization. To facilitate exploration and avoid local optima, we introduce stochasticity into the states. To mitigate sensitive gradients through high-dimensional vision-based world models, we modify the gradient structure to descend towards valid plans while only requiring action-input gradients. Our planner, which we call GRASP (Gradient RelAxed Stochastic Planner), can be viewed as a stochastic version of a non-condensed or collocation-based optimal controller. We provide theoretical justification and experiments on video-based world models, where our resulting planner outperforms existing planning algorithms like the cross-entropy method (CEM) and vanilla gradient-based optimization (GD) on long-horizon experiments, both in success rate and time to convergence.

Action-Minimization Meets Generative Modeling: Efficient Transition Path Sampling with the Onsager-Machlup Functional

Transition path sampling (TPS), which involves finding probable paths connecting two points on an energy landscape, remains a challenge due to the complexity of real-world atomistic systems. Current machine learning approaches use expensive, task-specific, and data-free training procedures, limiting their ability to benefit from recent advances in atomistic machine learning, such as high-quality datasets and large-scale pre-trained models. In this work, we address TPS by interpreting candidate paths as trajectories sampled from stochastic dynamics induced by the learned score function of pre-trained generative models, specifically denoising diffusion and flow matching. Under these dynamics, finding high-likelihood transition paths becomes equivalent to minimizing the Onsager-Machlup (OM) action functional. This enables us to repurpose pre-trained generative models for TPS in a zero-shot manner, in contrast with bespoke, task-specific TPS models trained in previous work. We demonstrate our approach on varied molecular systems, obtaining diverse, physically realistic transition pathways and generalizing beyond the pre-trained model's original training dataset. Our method can be easily incorporated into new generative models, making it practically relevant as models continue to scale and improve with increased data availability.

Learning a Diffusion Model Policy from Rewards via Q-Score Matching

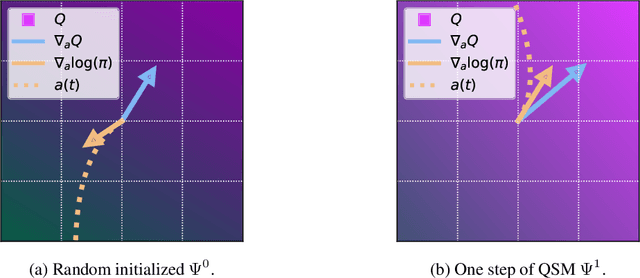
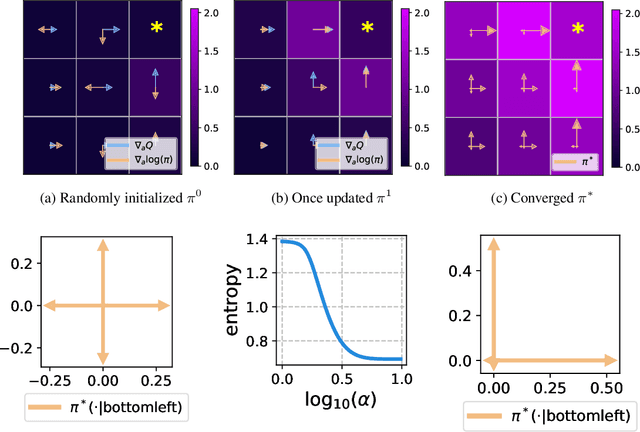
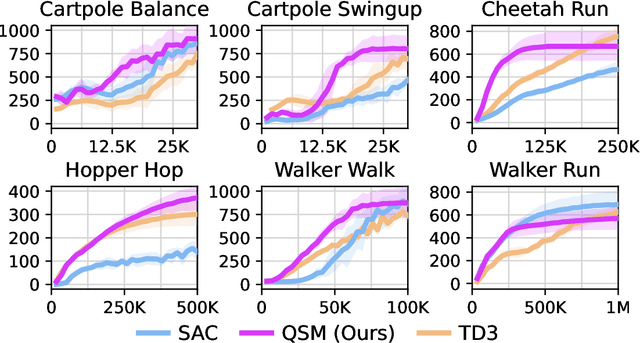
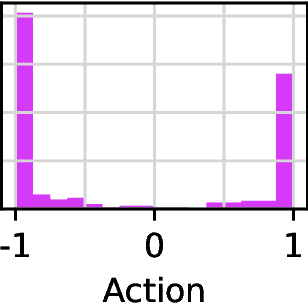
Diffusion models have become a popular choice for representing actor policies in behavior cloning and offline reinforcement learning. This is due to their natural ability to optimize an expressive class of distributions over a continuous space. However, previous works fail to exploit the score-based structure of diffusion models, and instead utilize a simple behavior cloning term to train the actor, limiting their ability in the actor-critic setting. In this paper, we focus on off-policy reinforcement learning and propose a new method for learning a diffusion model policy that exploits the linked structure between the score of the policy and the action gradient of the Q-function. We denote this method Q-score matching and provide theoretical justification for this approach. We conduct experiments in simulated environments to demonstrate the effectiveness of our proposed method and compare to popular baselines.

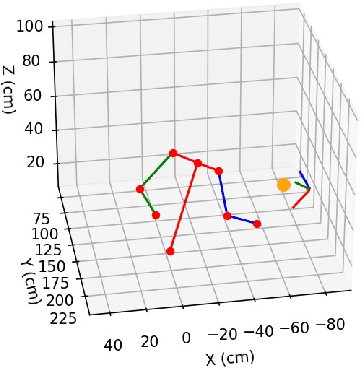
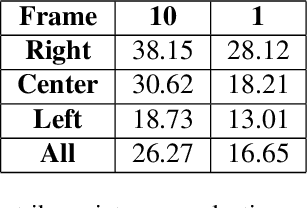
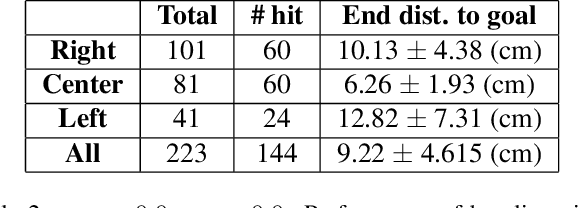
Role of Uncertainty in Anticipatory Trajectory Prediction for a Ping-Pong Playing Robot

Robotic interaction in fast-paced environments presents a substantial challenge, particularly in tasks requiring the prediction of dynamic, non-stationary objects for timely and accurate responses. An example of such a task is ping-pong, where the physical limitations of a robot may prevent it from reaching its goal in the time it takes the ball to cross the table. The scene of a ping-pong match contains rich visual information of a player's movement that can allow future game state prediction, with varying degrees of uncertainty. To this aim, we present a visual modeling, prediction, and control system to inform a ping-pong playing robot utilizing visual model uncertainty to allow earlier motion of the robot throughout the game. We present demonstrations and metrics in simulation to show the benefit of incorporating model uncertainty, the limitations of current standard model uncertainty estimators, and the need for more verifiable model uncertainty estimation. Our code is publicly available.

Representation Learning via Manifold Flattening and Reconstruction

This work proposes an algorithm for explicitly constructing a pair of neural networks that linearize and reconstruct an embedded submanifold, from finite samples of this manifold. Our such-generated neural networks, called Flattening Networks (FlatNet), are theoretically interpretable, computationally feasible at scale, and generalize well to test data, a balance not typically found in manifold-based learning methods. We present empirical results and comparisons to other models on synthetic high-dimensional manifold data and 2D image data. Our code is publicly available.

Pursuit of a Discriminative Representation for Multiple Subspaces via Sequential Games

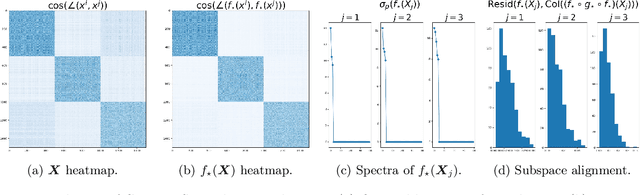
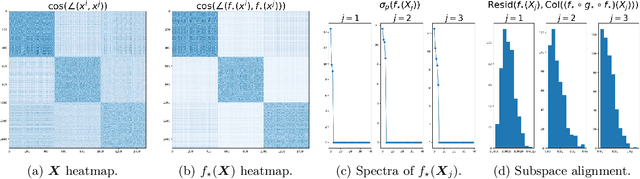
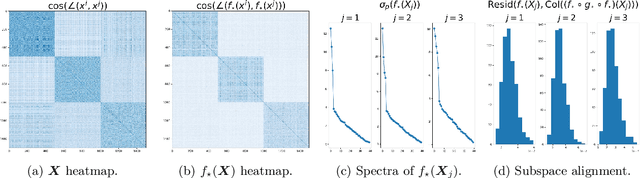
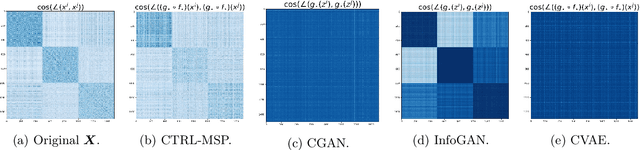
We consider the problem of learning discriminative representations for data in a high-dimensional space with distribution supported on or around multiple low-dimensional linear subspaces. That is, we wish to compute a linear injective map of the data such that the features lie on multiple orthogonal subspaces. Instead of treating this learning problem using multiple PCAs, we cast it as a sequential game using the closed-loop transcription (CTRL) framework recently proposed for learning discriminative and generative representations for general low-dimensional submanifolds. We prove that the equilibrium solutions to the game indeed give correct representations. Our approach unifies classical methods of learning subspaces with modern deep learning practice, by showing that subspace learning problems may be provably solved using the modern toolkit of representation learning. In addition, our work provides the first theoretical justification for the CTRL framework, in the important case of linear subspaces. We support our theoretical findings with compelling empirical evidence. We also generalize the sequential game formulation to more general representation learning problems. Our code, including methods for easy reproduction of experimental results, is publically available on GitHub.

Closed-Loop Data Transcription to an LDR via Minimaxing Rate Reduction

This work proposes a new computational framework for learning an explicit generative model for real-world datasets. In particular we propose to learn {\em a closed-loop transcription} between a multi-class multi-dimensional data distribution and a { linear discriminative representation (LDR)} in the feature space that consists of multiple independent multi-dimensional linear subspaces. In particular, we argue that the optimal encoding and decoding mappings sought can be formulated as the equilibrium point of a {\em two-player minimax game between the encoder and decoder}. A natural utility function for this game is the so-called {\em rate reduction}, a simple information-theoretic measure for distances between mixtures of subspace-like Gaussians in the feature space. Our formulation draws inspiration from closed-loop error feedback from control systems and avoids expensive evaluating and minimizing approximated distances between arbitrary distributions in either the data space or the feature space. To a large extent, this new formulation unifies the concepts and benefits of Auto-Encoding and GAN and naturally extends them to the settings of learning a {\em both discriminative and generative} representation for multi-class and multi-dimensional real-world data. Our extensive experiments on many benchmark imagery datasets demonstrate tremendous potential of this new closed-loop formulation: under fair comparison, visual quality of the learned decoder and classification performance of the encoder is competitive and often better than existing methods based on GAN, VAE, or a combination of both. We notice that the so learned features of different classes are explicitly mapped onto approximately {\em independent principal subspaces} in the feature space; and diverse visual attributes within each class are modeled by the {\em independent principal components} within each subspace.