Decentralized Learning in General-sum Markov Games

The Markov game framework is widely used to model interactions among agents with heterogeneous utilities in dynamic and uncertain societal-scale systems. In these systems, agents typically operate in a decentralized manner due to privacy and scalability concerns, often acting without any information about other agents. The design and analysis of decentralized learning algorithms that provably converge to rational outcomes remain elusive, especially beyond Markov zero-sum games and Markov potential games, which do not adequately capture the nature of many real-world interactions that is neither fully competitive nor fully cooperative. This paper investigates the design of decentralized learning algorithms for general-sum Markov games, aiming to provide provable guarantees of convergence to approximate Nash equilibria in the long run. Our approach builds on constructing a Markov Near-Potential Function (MNPF) to address the intractability of designing algorithms that converge to exact Nash equilibria. We demonstrate that MNPFs play a central role in ensuring the convergence of an actor-critic-based decentralized learning algorithm to approximate Nash equilibria. By leveraging a two-timescale approach, where Q-function estimates are updated faster than policy updates, we show that the system converges to a level set of the MNPF over the set of approximate Nash equilibria. This convergence result is further strengthened if the set of Nash equilibria is assumed to be finite. Our findings provide a new perspective on the analysis and design of decentralized learning algorithms in multi-agent systems.

Markov $α$-Potential Games: Equilibrium Approximation and Regret Analysis

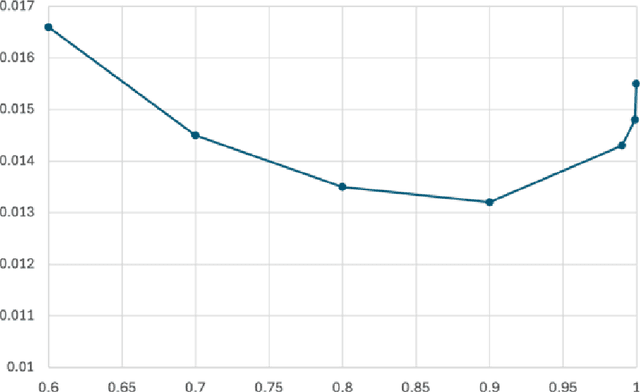
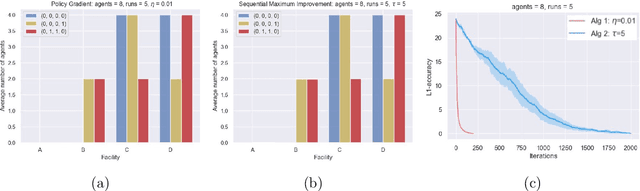
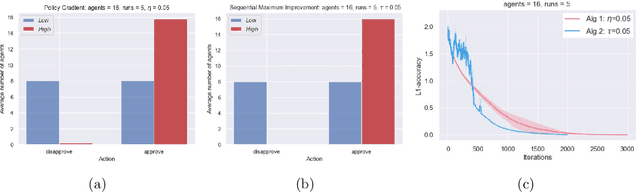
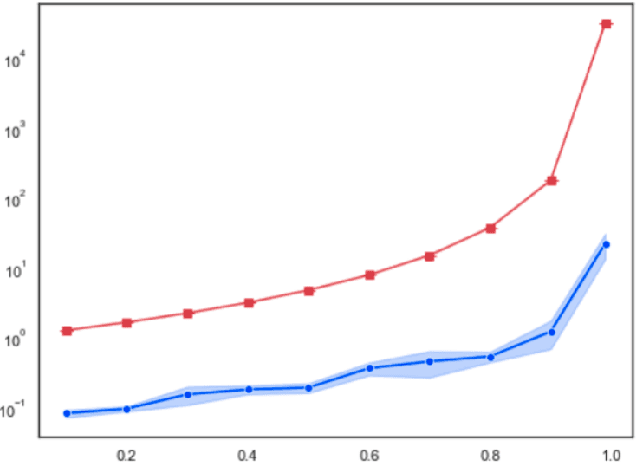
This paper proposes a new framework to study multi-agent interaction in Markov games: Markov $\alpha$-potential games. Markov potential games are special cases of Markov $\alpha$-potential games, so are two important and practically significant classes of games: Markov congestion games and perturbed Markov team games. In this paper, {$\alpha$-potential} functions for both games are provided and the gap $\alpha$ is characterized with respect to game parameters. Two algorithms -- the projected gradient-ascent algorithm and the sequential maximum improvement smoothed best response dynamics -- are introduced for approximating the stationary Nash equilibrium in Markov $\alpha$-potential games. The Nash-regret for each algorithm is shown to scale sub-linearly in time horizon. Our analysis and numerical experiments demonstrates that simple algorithms are capable of finding approximate equilibrium in Markov $\alpha$-potential games.

Pursuit of a Discriminative Representation for Multiple Subspaces via Sequential Games

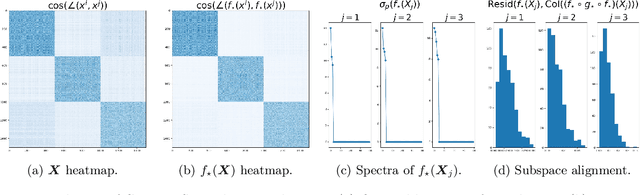
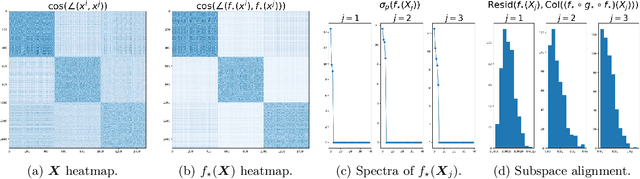
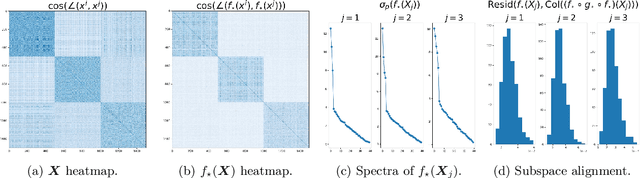
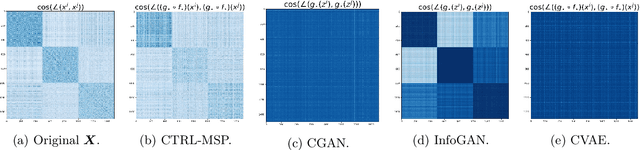
We consider the problem of learning discriminative representations for data in a high-dimensional space with distribution supported on or around multiple low-dimensional linear subspaces. That is, we wish to compute a linear injective map of the data such that the features lie on multiple orthogonal subspaces. Instead of treating this learning problem using multiple PCAs, we cast it as a sequential game using the closed-loop transcription (CTRL) framework recently proposed for learning discriminative and generative representations for general low-dimensional submanifolds. We prove that the equilibrium solutions to the game indeed give correct representations. Our approach unifies classical methods of learning subspaces with modern deep learning practice, by showing that subspace learning problems may be provably solved using the modern toolkit of representation learning. In addition, our work provides the first theoretical justification for the CTRL framework, in the important case of linear subspaces. We support our theoretical findings with compelling empirical evidence. We also generalize the sequential game formulation to more general representation learning problems. Our code, including methods for easy reproduction of experimental results, is publically available on GitHub.

Independent and Decentralized Learning in Markov Potential Games

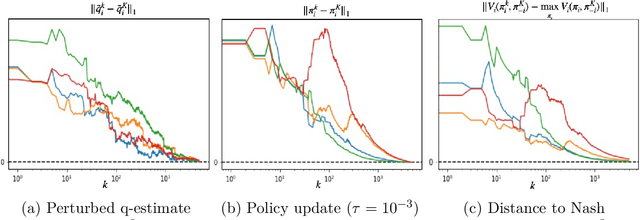
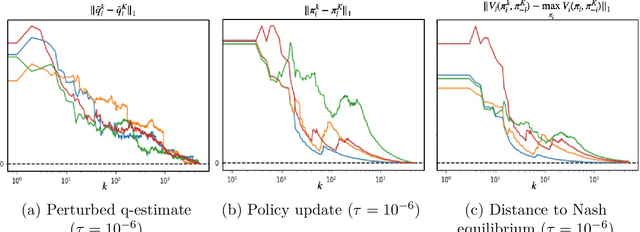
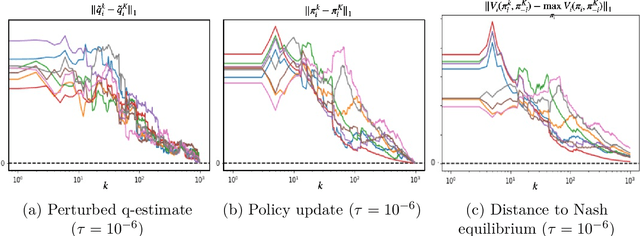
We propose a multi-agent reinforcement learning dynamics, and analyze its convergence properties in infinite-horizon discounted Markov potential games. We focus on the independent and decentralized setting, where players can only observe the realized state and their own reward in every stage. Players do not have knowledge of the game model, and cannot coordinate with each other. In each stage of our learning dynamics, players update their estimate of a perturbed Q-function that evaluates their total contingent payoff based on the realized one-stage reward in an asynchronous manner. Then, players independently update their policies by incorporating a smoothed optimal one-stage deviation strategy based on the estimated Q-function. A key feature of the learning dynamics is that the Q-function estimates are updated at a faster timescale than the policies. We prove that the policies induced by our learning dynamics converge to a stationary Nash equilibrium in Markov potential games with probability 1. Our results build on the theory of two timescale asynchronous stochastic approximation, and new analysis on the monotonicity of potential function along the trajectory of policy updates in Markov potential games.

Interpretable Machine Learning Models for Modal Split Prediction in Transportation Systems

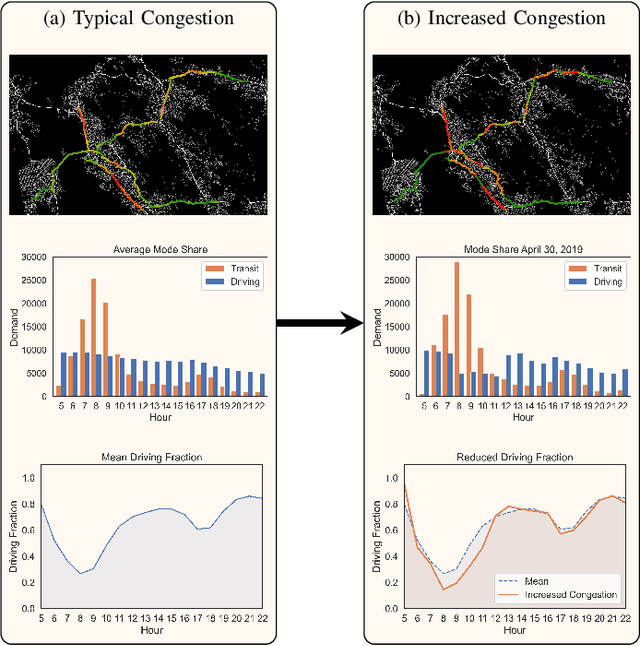
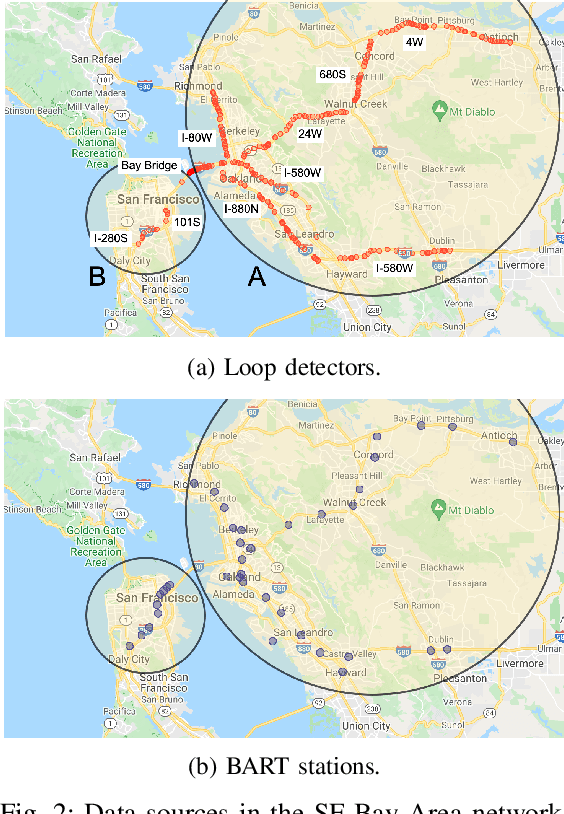
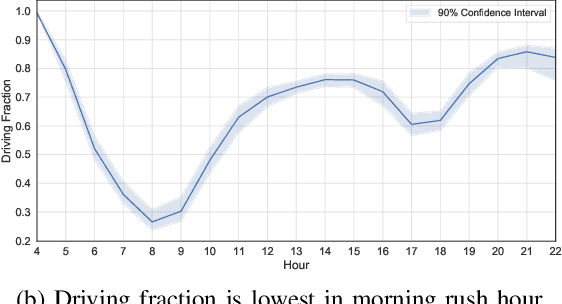
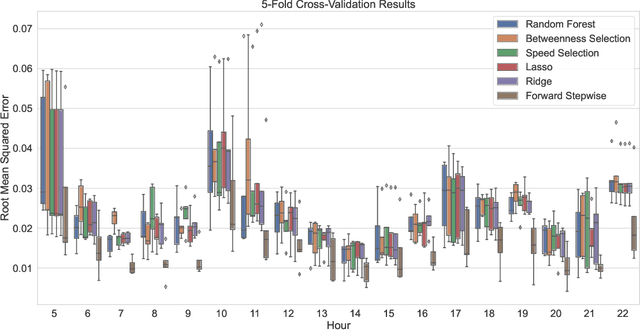
Modal split prediction in transportation networks has the potential to support network operators in managing traffic congestion and improving transit service reliability. We focus on the problem of hourly prediction of the fraction of travelers choosing one mode of transportation over another using high-dimensional travel time data. We use logistic regression as base model and employ various regularization techniques for variable selection to prevent overfitting and resolve multicollinearity issues. Importantly, we interpret the prediction accuracy results with respect to the inherent variability of modal splits and travelers' aggregate responsiveness to changes in travel time. By visualizing model parameters, we conclude that the subset of segments found important for predictive accuracy changes from hour-to-hour and include segments that are topologically central and/or highly congested. We apply our approach to the San Francisco Bay Area freeway and rapid transit network and demonstrate superior prediction accuracy and interpretability of our method compared to pre-specified variable selection methods.

Multi-agent Bayesian Learning with Adaptive Strategies: Convergence and Stability

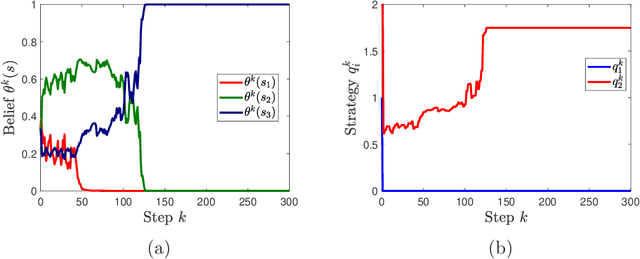
We study learning dynamics induced by strategic agents who repeatedly play a game with an unknown payoff-relevant parameter. In each step, an information system estimates a belief distribution of the parameter based on the players' strategies and realized payoffs using Bayes' rule. Players adjust their strategies by accounting for an equilibrium strategy or a best response strategy based on the updated belief. We prove that beliefs and strategies converge to a fixed point with probability 1. We also provide conditions that guarantee local and global stability of fixed points. Any fixed point belief consistently estimates the payoff distribution given the fixed point strategy profile. However, convergence to a complete information Nash equilibrium is not always guaranteed. We provide a sufficient and necessary condition under which fixed point belief recovers the unknown parameter. We also provide a sufficient condition for convergence to complete information equilibrium even when parameter learning is incomplete.