Population-Proportional Preference Learning from Human Feedback: An Axiomatic Approach

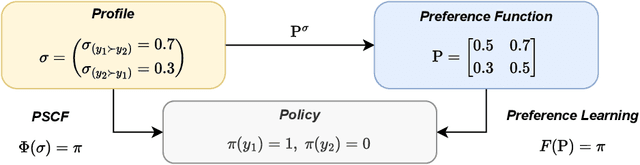
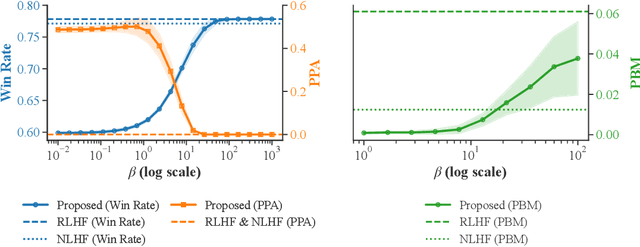
Conventional preference learning methods often prioritize opinions held more widely when aggregating preferences from multiple evaluators. This may result in policies that are biased in favor of some types of opinions or groups. The objective of this paper is to develop a novel preference learning framework capable of aligning aggregate opinions and policies proportionally with the true population distribution of evaluator preferences. Our approach infers the feasible set of evaluator population distributions directly from pairwise comparison data. Using these estimates, the algorithm constructs a policy that satisfies foundational axioms from social choice theory, namely monotonicity and Pareto efficiency, as well as our newly-introduced axioms of population-proportional representation and population-bounded robustness. We propose a soft-max relaxation method that smoothly trade-offs population-proportional representation with the selection of the Condorcet winner (which beats all other options in pairwise comparisons). Finally, we validate the effectiveness and scalability of our approach through experiments on both tabular recommendation tasks and large-scale language model alignment.

What Data Enables Optimal Decisions? An Exact Characterization for Linear Optimization

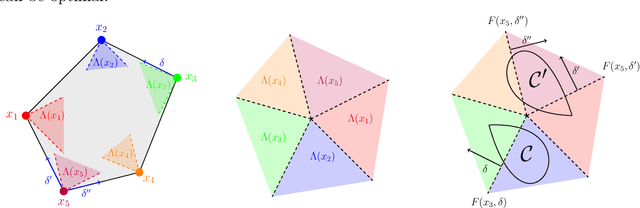
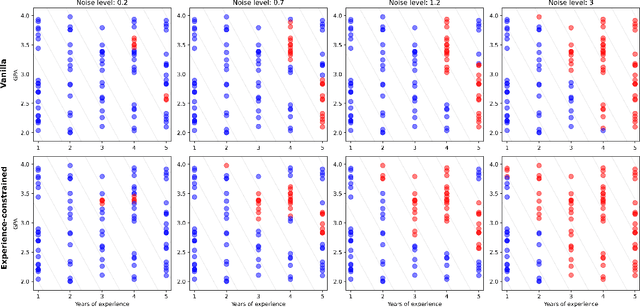
We study the fundamental question of how informative a dataset is for solving a given decision-making task. In our setting, the dataset provides partial information about unknown parameters that influence task outcomes. Focusing on linear programs, we characterize when a dataset is sufficient to recover an optimal decision, given an uncertainty set on the cost vector. Our main contribution is a sharp geometric characterization that identifies the directions of the cost vector that matter for optimality, relative to the task constraints and uncertainty set. We further develop a practical algorithm that, for a given task, constructs a minimal or least-costly sufficient dataset. Our results reveal that small, well-chosen datasets can often fully determine optimal decisions -- offering a principled foundation for task-aware data selection.

UFT: Unifying Supervised and Reinforcement Fine-Tuning

Post-training has demonstrated its importance in enhancing the reasoning capabilities of large language models (LLMs). The primary post-training methods can be categorized into supervised fine-tuning (SFT) and reinforcement fine-tuning (RFT). SFT is efficient and well-suited for small language models, but it may lead to overfitting and limit the reasoning abilities of larger models. In contrast, RFT generally yields better generalization but depends heavily on the strength of the base model. To address the limitations of SFT and RFT, we propose Unified Fine-Tuning (UFT), a novel post-training paradigm that unifies SFT and RFT into a single, integrated process. UFT enables the model to effectively explore solutions while incorporating informative supervision signals, bridging the gap between memorizing and thinking underlying existing methods. Notably, UFT outperforms both SFT and RFT in general, regardless of model sizes. Furthermore, we theoretically prove that UFT breaks RFT's inherent exponential sample complexity bottleneck, showing for the first time that unified training can exponentially accelerate convergence on long-horizon reasoning tasks.

Differentially Private Equilibrium Finding in Polymatrix Games

We study equilibrium finding in polymatrix games under differential privacy constraints. To start, we show that high accuracy and asymptotically vanishing differential privacy budget (as the number of players goes to infinity) cannot be achieved simultaneously under either of the two settings: (i) We seek to establish equilibrium approximation guarantees in terms of Euclidean distance to the equilibrium set, and (ii) the adversary has access to all communication channels. Then, assuming the adversary has access to a constant number of communication channels, we develop a novel distributed algorithm that recovers strategies with simultaneously vanishing Nash gap (in expected utility, also referred to as exploitability and privacy budget as the number of players increases.

MAPoRL: Multi-Agent Post-Co-Training for Collaborative Large Language Models with Reinforcement Learning

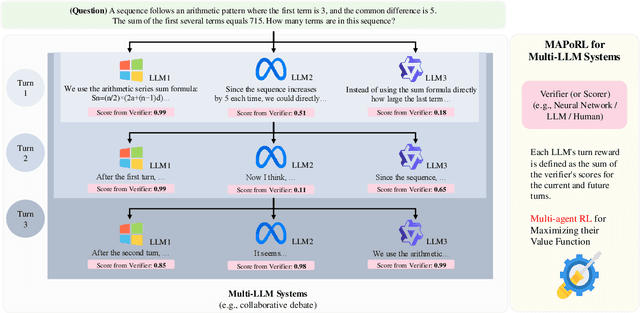
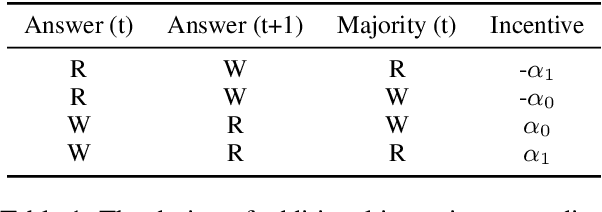
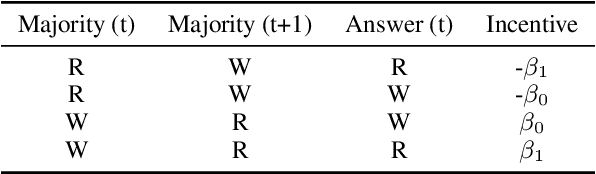
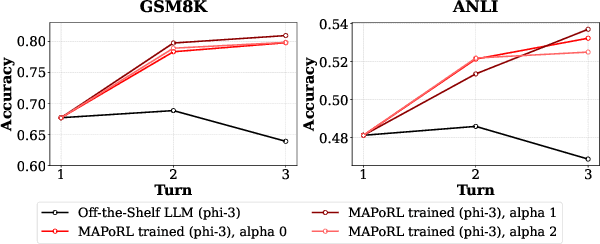
Leveraging multiple large language models (LLMs) to build collaborative multi-agentic workflows has demonstrated significant potential. However, most previous studies focus on prompting the out-of-the-box LLMs, relying on their innate capability for collaboration, which may not improve LLMs' performance as shown recently. In this paper, we introduce a new post-training paradigm MAPoRL (Multi-Agent Post-co-training for collaborative LLMs with Reinforcement Learning), to explicitly elicit the collaborative behaviors and further unleash the power of multi-agentic LLM frameworks. In MAPoRL, multiple LLMs first generate their own responses independently and engage in a multi-turn discussion to collaboratively improve the final answer. In the end, a MAPoRL verifier evaluates both the answer and the discussion, by assigning a score that verifies the correctness of the answer, while adding incentives to encourage corrective and persuasive discussions. The score serves as the co-training reward, and is then maximized through multi-agent RL. Unlike existing LLM post-training paradigms, MAPoRL advocates the co-training of multiple LLMs together using RL for better generalization. Accompanied by analytical insights, our experiments demonstrate that training individual LLMs alone is insufficient to induce effective collaboration. In contrast, multi-agent co-training can boost the collaboration performance across benchmarks, with generalization to unseen domains.

Last-Iterate Convergence of Payoff-Based Independent Learning in Zero-Sum Stochastic Games

In this paper, we consider two-player zero-sum matrix and stochastic games and develop learning dynamics that are payoff-based, convergent, rational, and symmetric between the two players. Specifically, the learning dynamics for matrix games are based on the smoothed best-response dynamics, while the learning dynamics for stochastic games build upon those for matrix games, with additional incorporation of the minimax value iteration. To our knowledge, our theoretical results present the first finite-sample analysis of such learning dynamics with last-iterate guarantees. In the matrix game setting, the results imply a sample complexity of $O(\epsilon^{-1})$ to find the Nash distribution and a sample complexity of $O(\epsilon^{-8})$ to find a Nash equilibrium. In the stochastic game setting, the results also imply a sample complexity of $O(\epsilon^{-8})$ to find a Nash equilibrium. To establish these results, the main challenge is to handle stochastic approximation algorithms with multiple sets of coupled and stochastic iterates that evolve on (possibly) different time scales. To overcome this challenge, we developed a coupled Lyapunov-based approach, which may be of independent interest to the broader community studying the convergence behavior of stochastic approximation algorithms.

A Policy-Gradient Approach to Solving Imperfect-Information Games with Iterate Convergence

Policy gradient methods have become a staple of any single-agent reinforcement learning toolbox, due to their combination of desirable properties: iterate convergence, efficient use of stochastic trajectory feedback, and theoretically-sound avoidance of importance sampling corrections. In multi-agent imperfect-information settings (extensive-form games), however, it is still unknown whether the same desiderata can be guaranteed while retaining theoretical guarantees. Instead, sound methods for extensive-form games rely on approximating counterfactual values (as opposed to Q values), which are incompatible with policy gradient methodologies. In this paper, we investigate whether policy gradient can be safely used in two-player zero-sum imperfect-information extensive-form games (EFGs). We establish positive results, showing for the first time that a policy gradient method leads to provable best-iterate convergence to a regularized Nash equilibrium in self-play.

Finite-Sample Guarantees for Best-Response Learning Dynamics in Zero-Sum Matrix Games

We study best-response type learning dynamics for two player zero-sum matrix games. We consider two settings that are distinguished by the type of information that each player has about the game and their opponent's strategy. The first setting is the full information case, in which each player knows their own and the opponent's payoff matrices and observes the opponent's mixed strategy. The second setting is the minimal information case, where players do not observe the opponent's strategy and are not aware of either of the payoff matrices (instead they only observe their realized payoffs). For this setting, also known as the radically uncoupled case in the learning in games literature, we study a two-timescale learning dynamics that combine smoothed best-response type updates for strategy estimates with a TD-learning update to estimate a local payoff function. For these dynamics, without additional exploration, we provide polynomial-time finite-sample guarantees for convergence to an $\epsilon$-Nash equilibrium.

LiteEFG: An Efficient Python Library for Solving Extensive-form Games

LiteEFG is an efficient library with easy-to-use Python bindings, which can solve multiplayer extensive-form games (EFGs). LiteEFG enables the user to express computation graphs in Python to define updates on the game tree structure. The graph is then executed by the C++ backend, leading to significant speedups compared to running the algorithm in Python. Moreover, in LiteEFG, the user needs to only specify the computation graph of the update rule in a decision node of the game, and LiteEFG will automatically distribute the update rule to each decision node and handle the structure of the imperfect-information game.

A Unified Linear Programming Framework for Offline Reward Learning from Human Demonstrations and Feedback

Inverse Reinforcement Learning (IRL) and Reinforcement Learning from Human Feedback (RLHF) are pivotal methodologies in reward learning, which involve inferring and shaping the underlying reward function of sequential decision-making problems based on observed human demonstrations and feedback. Most prior work in reward learning has relied on prior knowledge or assumptions about decision or preference models, potentially leading to robustness issues. In response, this paper introduces a novel linear programming (LP) framework tailored for offline reward learning. Utilizing pre-collected trajectories without online exploration, this framework estimates a feasible reward set from the primal-dual optimality conditions of a suitably designed LP, and offers an optimality guarantee with provable sample efficiency. Our LP framework also enables aligning the reward functions with human feedback, such as pairwise trajectory comparison data, while maintaining computational tractability and sample efficiency. We demonstrate that our framework potentially achieves better performance compared to the conventional maximum likelihood estimation (MLE) approach through analytical examples and numerical experiments.