Modular and Adaptive Conformal Prediction for Sequential Models via Residual Decomposition

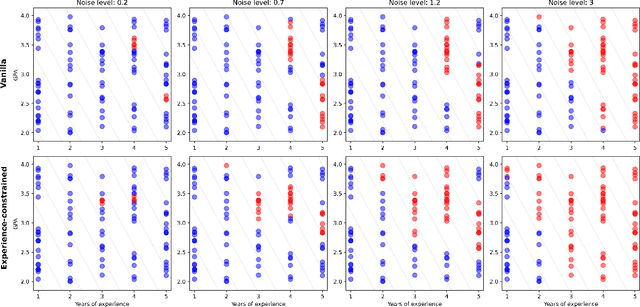
Conformal prediction offers finite-sample coverage guarantees under minimal assumptions. However, existing methods treat the entire modeling process as a black box, overlooking opportunities to exploit modular structure. We introduce a conformal prediction framework for two-stage sequential models, where an upstream predictor generates intermediate representations for a downstream model. By decomposing the overall prediction residual into stage-specific components, our method enables practitioners to attribute uncertainty to specific pipeline stages. We develop a risk-controlled parameter selection procedure using family-wise error rate (FWER) control to calibrate stage-wise scaling parameters, and propose an adaptive extension for non-stationary settings that preserves long-run coverage guarantees. Experiments on synthetic distribution shifts, as well as real-world supply chain and stock market data, demonstrate that our approach maintains coverage under conditions that degrade standard conformal methods, while providing interpretable stage-wise uncertainty attribution. This framework offers diagnostic advantages and robust coverage that standard conformal methods lack.

What Data Enables Optimal Decisions? An Exact Characterization for Linear Optimization

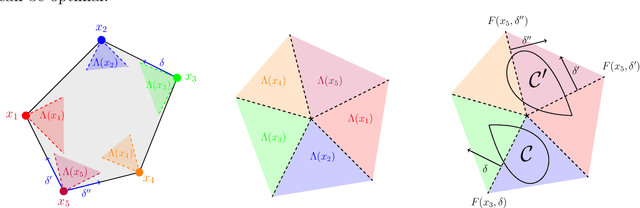
We study the fundamental question of how informative a dataset is for solving a given decision-making task. In our setting, the dataset provides partial information about unknown parameters that influence task outcomes. Focusing on linear programs, we characterize when a dataset is sufficient to recover an optimal decision, given an uncertainty set on the cost vector. Our main contribution is a sharp geometric characterization that identifies the directions of the cost vector that matter for optimality, relative to the task constraints and uncertainty set. We further develop a practical algorithm that, for a given task, constructs a minimal or least-costly sufficient dataset. Our results reveal that small, well-chosen datasets can often fully determine optimal decisions -- offering a principled foundation for task-aware data selection.

A Deep Generative Learning Approach for Two-stage Adaptive Robust Optimization

Two-stage adaptive robust optimization is a powerful approach for planning under uncertainty that aims to balance costs of "here-and-now" first-stage decisions with those of "wait-and-see" recourse decisions made after uncertainty is realized. To embed robustness against uncertainty, modelers typically assume a simple polyhedral or ellipsoidal set over which contingencies may be realized. However, these simple uncertainty sets tend to yield highly conservative decision-making when uncertainties are high-dimensional. In this work, we introduce AGRO, a column-and-constraint generation algorithm that performs adversarial generation for two-stage adaptive robust optimization using a variational autoencoder. AGRO identifies realistic and cost-maximizing contingencies by optimizing over spherical uncertainty sets in a latent space using a projected gradient ascent approach that differentiates the optimal recourse cost with respect to the latent variable. To demonstrate the cost- and time-efficiency of our approach experimentally, we apply AGRO to an adaptive robust capacity expansion problem for a regional power system and show that AGRO is able to reduce costs by up to 7.8% and runtimes by up to 77% in comparison to the conventional column-and-constraint generation algorithm.

Learning-assisted Stochastic Capacity Expansion Planning: A Bayesian Optimization Approach

Solving large-scale capacity expansion problems (CEPs) is central to cost-effective decarbonization of regional-scale energy systems. To ensure the intended outcomes of CEPs, modeling uncertainty due to weather-dependent variable renewable energy (VRE) supply and energy demand becomes crucially important. However, the resulting stochastic optimization models are often less computationally tractable than their deterministic counterparts. Here, we propose a learning-assisted approximate solution method to tractably solve two-stage stochastic CEPs. Our method identifies low-cost planning decisions by constructing and solving a sequence of tractable temporally aggregated surrogate problems. We adopt a Bayesian optimization approach to searching the space of time series aggregation hyperparameters and compute approximate solutions that minimize costs on a validation set of supply-demand projections. Importantly, we evaluate solved planning outcomes on a held-out set of test projections. We apply our approach to generation and transmission expansion planning for a joint power-gas system spanning New England. We show that our approach yields an estimated cost savings of up to 3.8% in comparison to benchmark time series aggregation approaches.

Uncertainty Informed Optimal Resource Allocation with Gaussian Process based Bayesian Inference

We focus on the problem of uncertainty informed allocation of medical resources (vaccines) to heterogeneous populations for managing epidemic spread. We tackle two related questions: (1) For a compartmental ordinary differential equation (ODE) model of epidemic spread, how can we estimate and integrate parameter uncertainty into resource allocation decisions? (2) How can we computationally handle both nonlinear ODE constraints and parameter uncertainties for a generic stochastic optimization problem for resource allocation? To the best of our knowledge current literature does not fully resolve these questions. Here, we develop a data-driven approach to represent parameter uncertainty accurately and tractably in a novel stochastic optimization problem formulation. We first generate a tractable scenario set by estimating the distribution on ODE model parameters using Bayesian inference with Gaussian processes. Next, we develop a parallelized solution algorithm that accounts for scenario-dependent nonlinear ODE constraints. Our scenario-set generation procedure and solution approach are flexible in that they can handle any compartmental epidemiological ODE model. Our computational experiments on two different non-linear ODE models (SEIR and SEPIHR) indicate that accounting for uncertainty in key epidemiological parameters can improve the efficacy of time-critical allocation decisions by 4-8%. This improvement can be attributed to data-driven and optimal (strategic) nature of vaccine allocations, especially in the early stages of the epidemic when the allocation strategy can crucially impact the long-term trajectory of the disease.

Learning Spatio-Temporal Aggregations for Large-Scale Capacity Expansion Problems

Effective investment planning decisions are crucial to ensure cyber-physical infrastructures satisfy performance requirements over an extended time horizon. Computing these decisions often requires solving Capacity Expansion Problems (CEPs). In the context of regional-scale energy systems, these problems are prohibitively expensive to solve due to large network sizes, heterogeneous node characteristics, and a large number of operational periods. To maintain tractability, traditional approaches aggregate network nodes and/or select a set of representative time periods. Often, these reductions do not capture supply-demand variations that crucially impact CEP costs and constraints, leading to suboptimal decisions. Here, we propose a novel graph convolutional autoencoder approach for spatio-temporal aggregation of a generic CEP with heterogeneous nodes (CEPHN). Our architecture leverages graph pooling to identify nodes with similar characteristics and minimizes a multi-objective loss function. This loss function is tailored to induce desirable spatial and temporal aggregations with regard to tractability and optimality. In particular, the output of the graph pooling provides a spatial aggregation while clustering the low-dimensional encoded representations yields a temporal aggregation. We apply our approach to generation expansion planning of a coupled 88-node power and natural gas system in New England. The resulting aggregation leads to a simpler CEPHN with 6 nodes and a small set of representative days selected from one year. We evaluate aggregation outcomes over a range of hyperparameters governing the loss function and compare resulting upper bounds on the original problem with those obtained using benchmark methods. We show that our approach provides upper bounds that are 33% (resp. 10%) lower those than obtained from benchmark spatial (resp. temporal) aggregation approaches.

Effective Dimension in Bandit Problems under Censorship

In this paper, we study both multi-armed and contextual bandit problems in censored environments. Our goal is to estimate the performance loss due to censorship in the context of classical algorithms designed for uncensored environments. Our main contributions include the introduction of a broad class of censorship models and their analysis in terms of the effective dimension of the problem -- a natural measure of its underlying statistical complexity and main driver of the regret bound. In particular, the effective dimension allows us to maintain the structure of the original problem at first order, while embedding it in a bigger space, and thus naturally leads to results analogous to uncensored settings. Our analysis involves a continuous generalization of the Elliptical Potential Inequality, which we believe is of independent interest. We also discover an interesting property of decision-making under censorship: a transient phase during which initial misspecification of censorship is self-corrected at an extra cost, followed by a stationary phase that reflects the inherent slowdown of learning governed by the effective dimension. Our results are useful for applications of sequential decision-making models where the feedback received depends on strategic uncertainty (e.g., agents' willingness to follow a recommendation) and/or random uncertainty (e.g., loss or delay in arrival of information).

Graph Representation Learning for Energy Demand Data: Application to Joint Energy System Planning under Emissions Constraints

A rapid transformation of current electric power and natural gas (NG) infrastructure is imperative to meet the mid-century goal of CO2 emissions reduction requires. This necessitates a long-term planning of the joint power-NG system under representative demand and supply patterns, operational constraints, and policy considerations. Our work is motivated by the computational and practical challenges associated with solving the generation and transmission expansion problem (GTEP) for joint planning of power-NG systems. Specifically, we focus on efficiently extracting a set of representative days from power and NG data in respective networks and using this set to reduce the computational burden required to solve the GTEP. We propose a Graph Autoencoder for Multiple time resolution Energy Systems (GAMES) to capture the spatio-temporal demand patterns in interdependent networks and account for differences in the temporal resolution of available data. The resulting embeddings are used in a clustering algorithm to select representative days. We evaluate the effectiveness of our approach in solving a GTEP formulation calibrated for the joint power-NG system in New England. This formulation accounts for the physical interdependencies between power and NG systems, including the joint emissions constraint. Our results show that the set of representative days obtained from GAMES not only allows us to tractably solve the GTEP formulation, but also achieves a lower cost of implementing the joint planning decisions.

Interpretable Machine Learning Models for Modal Split Prediction in Transportation Systems

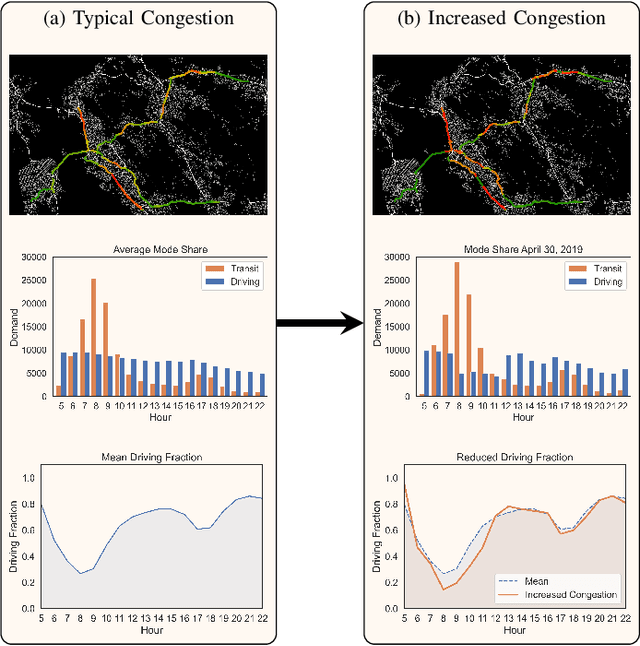
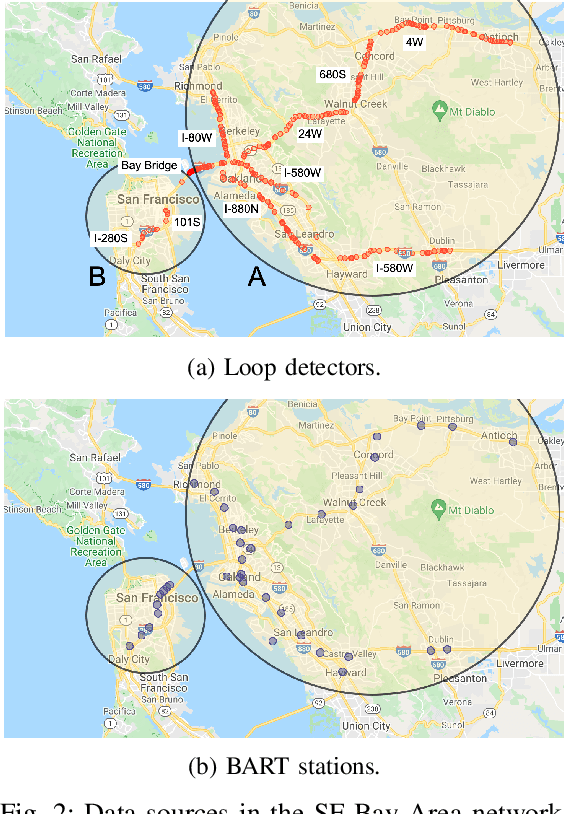
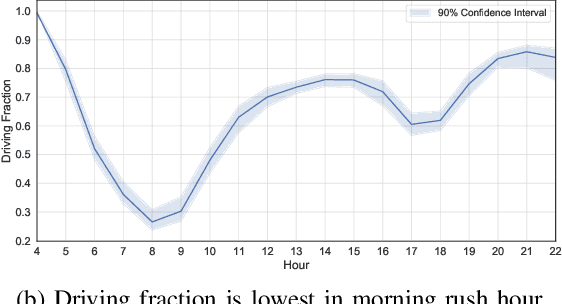
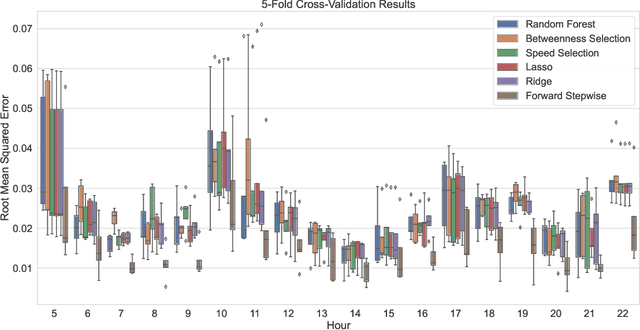
Modal split prediction in transportation networks has the potential to support network operators in managing traffic congestion and improving transit service reliability. We focus on the problem of hourly prediction of the fraction of travelers choosing one mode of transportation over another using high-dimensional travel time data. We use logistic regression as base model and employ various regularization techniques for variable selection to prevent overfitting and resolve multicollinearity issues. Importantly, we interpret the prediction accuracy results with respect to the inherent variability of modal splits and travelers' aggregate responsiveness to changes in travel time. By visualizing model parameters, we conclude that the subset of segments found important for predictive accuracy changes from hour-to-hour and include segments that are topologically central and/or highly congested. We apply our approach to the San Francisco Bay Area freeway and rapid transit network and demonstrate superior prediction accuracy and interpretability of our method compared to pre-specified variable selection methods.

Damage Estimation and Localization from Sparse Aerial Imagery

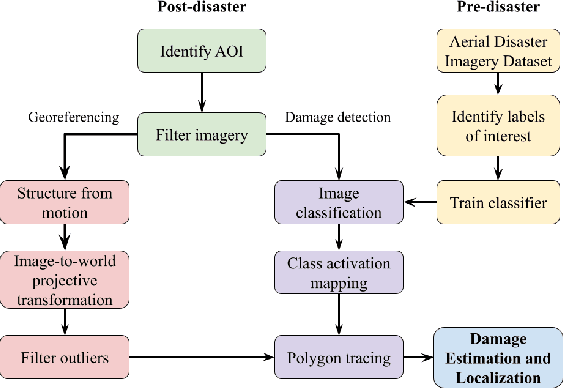
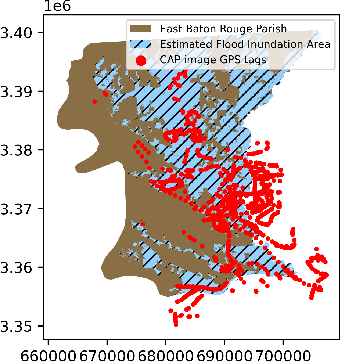
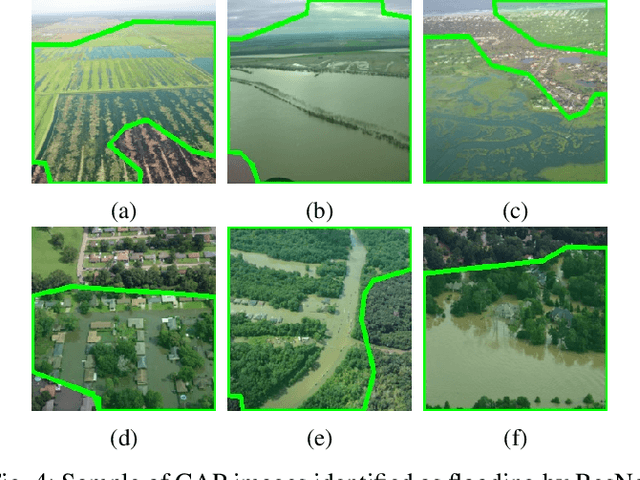
Aerial images provide important situational awareness for responding to natural disasters such as hurricanes. They are well-suited for providing information for damage estimation and localization (DEL); i.e., characterizing the type and spatial extent of damage following a disaster. Despite recent advances in sensing and unmanned aerial systems technology, much of post-disaster aerial imagery is still taken by handheld DSLR cameras from small, manned, fixed-wing aircraft. However, these handheld cameras lack IMU information, and images are taken opportunistically post-event by operators. As such, DEL from such imagery is still a highly manual and time-consuming process. We propose an approach to both detect damage in aerial images and localize it in world coordinates, with specific focus on detecting and localizing flooding. The approach is based on using structure from motion to relate image coordinates to world coordinates via a projective transformation, using class activation mapping to detect the extent of damage in an image, and applying the projective transformation to localize damage in world coordinates. We evaluate the performance of our approach on post-event data from the 2016 Louisiana floods, and find that our approach achieves a precision of 88%. Given this high precision using limited data, we argue that this approach is currently viable for fast and effective DEL from handheld aerial imagery for disaster response.