Multi-Query Shortest-Path Problem in Graphs of Convex Sets

The Shortest-Path Problem in Graph of Convex Sets (SPP in GCS) is a recently developed optimization framework that blends discrete and continuous decision making. Many relevant problems in robotics, such as collision-free motion planning, can be cast and solved as an SPP in GCS, yielding lower-cost solutions and faster runtimes than state-of-the-art algorithms. In this paper, we are motivated by motion planning of robot arms that must operate swiftly in static environments. We consider a multi-query extension of the SPP in GCS, where the goal is to efficiently precompute optimal paths between given sets of initial and target conditions. Our solution consists of two stages. Offline, we use semidefinite programming to compute a coarse lower bound on the problem's cost-to-go function. Then, online, this lower bound is used to incrementally generate feasible paths by solving short-horizon convex programs. For a robot arm with seven joints, our method designs higher quality trajectories up to two orders of magnitude faster than existing motion planners.

A Unified Linear Programming Framework for Offline Reward Learning from Human Demonstrations and Feedback

Inverse Reinforcement Learning (IRL) and Reinforcement Learning from Human Feedback (RLHF) are pivotal methodologies in reward learning, which involve inferring and shaping the underlying reward function of sequential decision-making problems based on observed human demonstrations and feedback. Most prior work in reward learning has relied on prior knowledge or assumptions about decision or preference models, potentially leading to robustness issues. In response, this paper introduces a novel linear programming (LP) framework tailored for offline reward learning. Utilizing pre-collected trajectories without online exploration, this framework estimates a feasible reward set from the primal-dual optimality conditions of a suitably designed LP, and offers an optimality guarantee with provable sample efficiency. Our LP framework also enables aligning the reward functions with human feedback, such as pairwise trajectory comparison data, while maintaining computational tractability and sample efficiency. We demonstrate that our framework potentially achieves better performance compared to the conventional maximum likelihood estimation (MLE) approach through analytical examples and numerical experiments.

Towards Tight Convex Relaxations for Contact-Rich Manipulation

We present a method for global motion planning of robotic systems that interact with the environment through contacts. Our method directly handles the hybrid nature of such tasks using tools from convex optimization. We formulate the motion-planning problem as a shortest-path problem in a graph of convex sets, where a path in the graph corresponds to a contact sequence and a convex set models the quasi-static dynamics within a fixed contact mode. For each contact mode, we use semidefinite programming to relax the nonconvex dynamics that results from the simultaneous optimization of the object's pose, contact locations, and contact forces. The result is a tight convex relaxation of the overall planning problem, that can be efficiently solved and quickly rounded to find a feasible contact-rich trajectory. As a first application of this technique, we focus on the task of planar pushing. Exhaustive experiments show that our convex-optimization method generates plans that are consistently within a small percentage of the global optimum. We demonstrate the quality of these plans on a real robotic system.

Kernel approximation on algebraic varieties

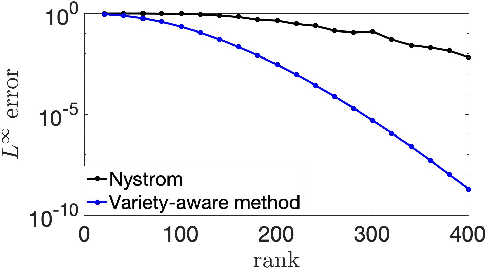
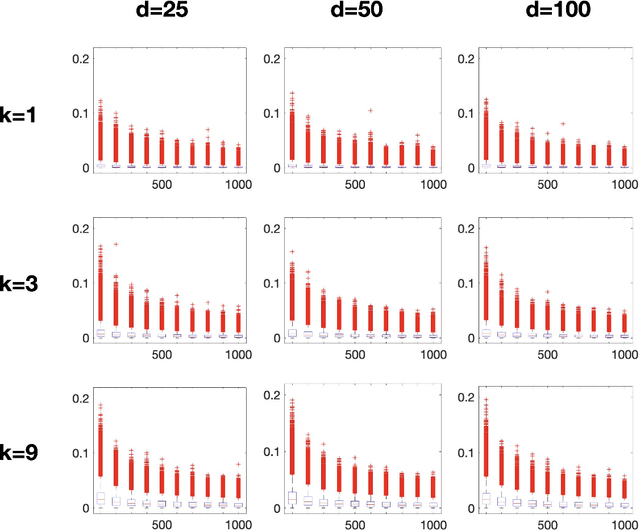
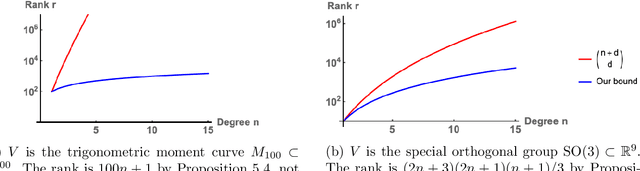
Low-rank approximation of kernels is a fundamental mathematical problem with widespread algorithmic applications. Often the kernel is restricted to an algebraic variety, e.g., in problems involving sparse or low-rank data. We show that significantly better approximations are obtainable in this setting: the rank required to achieve a given error depends on the variety's dimension rather than the ambient dimension, which is typically much larger. This is true in both high-precision and high-dimensional regimes. Our results are presented for smooth isotropic kernels, the predominant class of kernels used in applications. Our main technical insight is to approximate smooth kernels by polynomial kernels, and leverage two key properties of polynomial kernels that hold when they are restricted to a variety. First, their ranks decrease exponentially in the variety's co-dimension. Second, their maximum values are governed by their values over a small set of points. Together, our results provide a general approach for exploiting (approximate) "algebraic structure" in datasets in order to efficiently solve large-scale data science problems.

Convergence Rate of Block-Coordinate Maximization Burer-Monteiro Method for Solving Large SDPs

Semidefinite programming (SDP) with equality constraints arise in many optimization and machine learning problems, such as Max-Cut, community detection and robust PCA. Although SDPs can be solved to arbitrary precision in polynomial time, generic convex solvers do not scale well with the dimension of the problem. In order to address this issue, Burer and Monteiro \cite{burer2003nonlinear} proposed to reduce the dimension of the problem by appealing to a low-rank factorization, and solve the subsequent non-convex problem instead. It is well-understood that the resulting non-convex problem acts as a reliable surrogate to the original SDP, and can be efficiently solved using the block-coordinate maximization method. Despite its simplicity, remarkable success, and wide use in practice, the theoretical understanding of the convergence of this method is limited. We prove that the block-coordinate maximization algorithm applied to the non-convex Burer-Monteiro approach enjoys a global sublinear rate without any assumptions on the problem, and a local linear convergence rate despite no local maxima is locally strongly concave. We illustrate our results through examples and numerical experiments.

Rejoinder: Latent variable graphical model selection via convex optimization

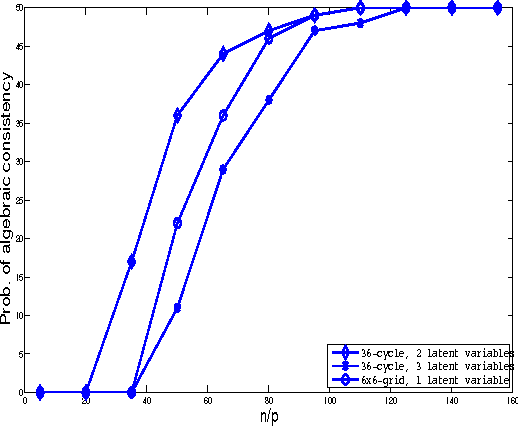
Rejoinder to "Latent variable graphical model selection via convex optimization" by Venkat Chandrasekaran, Pablo A. Parrilo and Alan S. Willsky [arXiv:1008.1290].