Modeling groundwater levels in California's Central Valley by hierarchical Gaussian process and neural network regression

Modeling groundwater levels continuously across California's Central Valley (CV) hydrological system is challenging due to low-quality well data which is sparsely and noisily sampled across time and space. A novel machine learning method is proposed for modeling groundwater levels by learning from a 3D lithological texture model of the CV aquifer. The proposed formulation performs multivariate regression by combining Gaussian processes (GP) and deep neural networks (DNN). Proposed hierarchical modeling approach constitutes training the DNN to learn a lithologically informed latent space where non-parametric regression with GP is performed. The methodology is applied for modeling groundwater levels across the CV during 2015 - 2020. We demonstrate the efficacy of GP-DNN regression for modeling non-stationary features in the well data with fast and reliable uncertainty quantification. Our results indicate that the 2017 and 2019 wet years in California were largely ineffective in replenishing the groundwater loss caused during previous drought years.

Optimal Convex and Nonconvex Regularizers for a Data Source

In optimization-based approaches to inverse problems and to statistical estimation, it is common to augment the objective with a regularizer to address challenges associated with ill-posedness. The choice of a suitable regularizer is typically driven by prior domain information and computational considerations. Convex regularizers are attractive as they are endowed with certificates of optimality as well as the toolkit of convex analysis, but exhibit a computational scaling that makes them ill-suited beyond moderate-sized problem instances. On the other hand, nonconvex regularizers can often be deployed at scale, but do not enjoy the certification properties associated with convex regularizers. In this paper, we seek a systematic understanding of the power and the limitations of convex regularization by investigating the following questions: Given a distribution, what are the optimal regularizers, both convex and nonconvex, for data drawn from the distribution? What properties of a data source govern whether it is amenable to convex regularization? We address these questions for the class of continuous and positively homogenous regularizers for which convex and nonconvex regularizers correspond, respectively, to convex bodies and star bodies. By leveraging dual Brunn-Minkowski theory, we show that a radial function derived from a data distribution is the key quantity for identifying optimal regularizers and for assessing the amenability of a data source to convex regularization. Using tools such as $\Gamma$-convergence, we show that our results are robust in the sense that the optimal regularizers for a sample drawn from a distribution converge to their population counterparts as the sample size grows large. Finally, we give generalization guarantees that recover previous results for polyhedral regularizers (i.e., dictionary learning) and lead to new ones for semidefinite regularizers.

Spectrahedral Regression

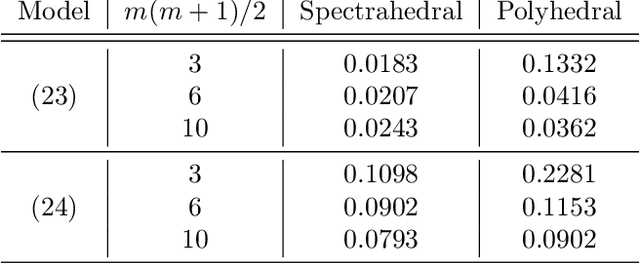
Convex regression is the problem of fitting a convex function to a data set consisting of input-output pairs. We present a new approach to this problem called spectrahedral regression, in which we fit a spectrahedral function to the data, i.e. a function that is the maximum eigenvalue of an affine matrix expression of the input. This method represents a significant generalization of polyhedral (also called max-affine) regression, in which a polyhedral function (a maximum of a fixed number of affine functions) is fit to the data. We prove bounds on how well spectrahedral functions can approximate arbitrary convex functions via statistical risk analysis. We also analyze an alternating minimization algorithm for the non-convex optimization problem of fitting the best spectrahedral function to a given data set. We show that this algorithm converges geometrically with high probability to a small ball around the optimal parameter given a good initialization. Finally, we demonstrate the utility of our approach with experiments on synthetic data sets as well as real data arising in applications such as economics and engineering design.

Learning Exponential Family Graphical Models with Latent Variables using Regularized Conditional Likelihood

Fitting a graphical model to a collection of random variables given sample observations is a challenging task if the observed variables are influenced by latent variables, which can induce significant confounding statistical dependencies among the observed variables. We present a new convex relaxation framework based on regularized conditional likelihood for latent-variable graphical modeling in which the conditional distribution of the observed variables conditioned on the latent variables is given by an exponential family graphical model. In comparison to previously proposed tractable methods that proceed by characterizing the marginal distribution of the observed variables, our approach is applicable in a broader range of settings as it does not require knowledge about the specific form of distribution of the latent variables and it can be specialized to yield tractable approaches to problems in which the observed data are not well-modeled as Gaussian. We demonstrate the utility and flexibility of our framework via a series of numerical experiments on synthetic as well as real data.

A Matrix Factorization Approach for Learning Semidefinite-Representable Regularizers

Regularization techniques are widely employed in optimization-based approaches for solving ill-posed inverse problems in data analysis and scientific computing. These methods are based on augmenting the objective with a penalty function, which is specified based on prior domain-specific expertise to induce a desired structure in the solution. We consider the problem of learning suitable regularization functions from data in settings in which precise domain knowledge is not directly available. Previous work under the title of `dictionary learning' or `sparse coding' may be viewed as learning a regularization function that can be computed via linear programming. We describe generalizations of these methods to learn regularizers that can be computed and optimized via semidefinite programming. Our framework for learning such semidefinite regularizers is based on obtaining structured factorizations of data matrices, and our algorithmic approach for computing these factorizations combines recent techniques for rank minimization problems along with an operator analog of Sinkhorn scaling. Under suitable conditions on the input data, our algorithm provides a locally linearly convergent method for identifying the correct regularizer that promotes the type of structure contained in the data. Our analysis is based on the stability properties of Operator Sinkhorn scaling and their relation to geometric aspects of determinantal varieties (in particular tangent spaces with respect to these varieties). The regularizers obtained using our framework can be employed effectively in semidefinite programming relaxations for solving inverse problems.

Rejoinder: Latent variable graphical model selection via convex optimization

Rejoinder to "Latent variable graphical model selection via convex optimization" by Venkat Chandrasekaran, Pablo A. Parrilo and Alan S. Willsky [arXiv:1008.1290].

Complexity of Inference in Graphical Models

It is well-known that inference in graphical models is hard in the worst case, but tractable for models with bounded treewidth. We ask whether treewidth is the only structural criterion of the underlying graph that enables tractable inference. In other words, is there some class of structures with unbounded treewidth in which inference is tractable? Subject to a combinatorial hypothesis due to Robertson et al. (1994), we show that low treewidth is indeed the only structural restriction that can ensure tractability. Thus, even for the "best case" graph structure, there is no inference algorithm with complexity polynomial in the treewidth.

Feedback Message Passing for Inference in Gaussian Graphical Models

While loopy belief propagation (LBP) performs reasonably well for inference in some Gaussian graphical models with cycles, its performance is unsatisfactory for many others. In particular for some models LBP does not converge, and in general when it does converge, the computed variances are incorrect (except for cycle-free graphs for which belief propagation (BP) is non-iterative and exact). In this paper we propose {\em feedback message passing} (FMP), a message-passing algorithm that makes use of a special set of vertices (called a {\em feedback vertex set} or {\em FVS}) whose removal results in a cycle-free graph. In FMP, standard BP is employed several times on the cycle-free subgraph excluding the FVS while a special message-passing scheme is used for the nodes in the FVS. The computational complexity of exact inference is $O(k^2n)$, where $k$ is the number of feedback nodes, and $n$ is the total number of nodes. When the size of the FVS is very large, FMP is intractable. Hence we propose {\em approximate FMP}, where a pseudo-FVS is used instead of an FVS, and where inference in the non-cycle-free graph obtained by removing the pseudo-FVS is carried out approximately using LBP. We show that, when approximate FMP converges, it yields exact means and variances on the pseudo-FVS and exact means throughout the remainder of the graph. We also provide theoretical results on the convergence and accuracy of approximate FMP. In particular, we prove error bounds on variance computation. Based on these theoretical results, we design efficient algorithms to select a pseudo-FVS of bounded size. The choice of the pseudo-FVS allows us to explicitly trade off between efficiency and accuracy. Experimental results show that using a pseudo-FVS of size no larger than $\log(n)$, this procedure converges much more often, more quickly, and provides more accurate results than LBP on the entire graph.