The Star Geometry of Critic-Based Regularizer Learning

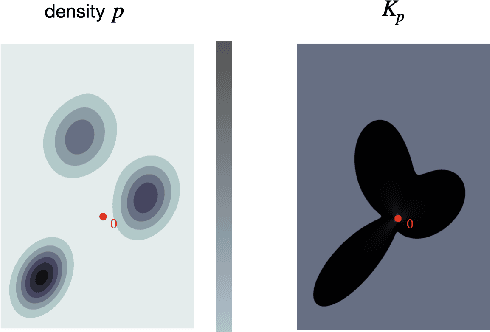
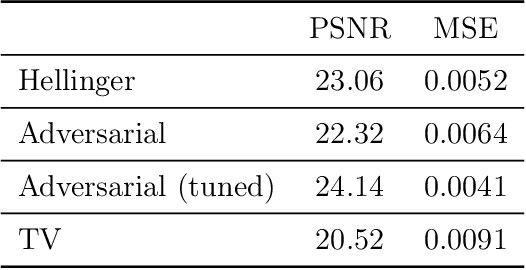
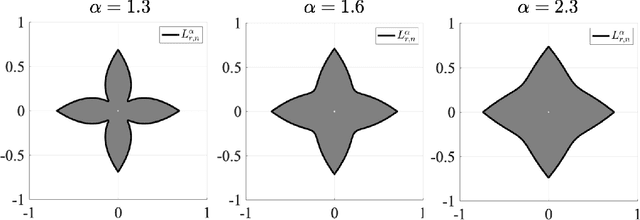
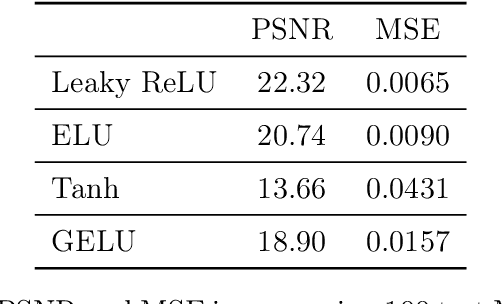
Variational regularization is a classical technique to solve statistical inference tasks and inverse problems, with modern data-driven approaches parameterizing regularizers via deep neural networks showcasing impressive empirical performance. Recent works along these lines learn task-dependent regularizers. This is done by integrating information about the measurements and ground-truth data in an unsupervised, critic-based loss function, where the regularizer attributes low values to likely data and high values to unlikely data. However, there is little theory about the structure of regularizers learned via this process and how it relates to the two data distributions. To make progress on this challenge, we initiate a study of optimizing critic-based loss functions to learn regularizers over a particular family of regularizers: gauges (or Minkowski functionals) of star-shaped bodies. This family contains regularizers that are commonly employed in practice and shares properties with regularizers parameterized by deep neural networks. We specifically investigate critic-based losses derived from variational representations of statistical distances between probability measures. By leveraging tools from star geometry and dual Brunn-Minkowski theory, we illustrate how these losses can be interpreted as dual mixed volumes that depend on the data distribution. This allows us to derive exact expressions for the optimal regularizer in certain cases. Finally, we identify which neural network architectures give rise to such star body gauges and when do such regularizers have favorable properties for optimization. More broadly, this work highlights how the tools of star geometry can aid in understanding the geometry of unsupervised regularizer learning.

Semidefinite Relaxations of the Gromov-Wasserstein Distance

The Gromov-Wasserstein (GW) distance is a variant of the optimal transport problem that allows one to match objects between incomparable spaces. At its core, the GW distance is specified as the solution of a non-convex quadratic program and is not known to be tractable to solve. In particular, existing solvers for the GW distance are only able to find locally optimal solutions. In this work, we propose a semi-definite programming (SDP) relaxation of the GW distance. The relaxation can be viewed as the dual of the GW distance augmented with constraints that relate the linear and quadratic terms of transportation maps. Our relaxation provides a principled manner to compute the approximation ratio of any transport map to the global optimal solution. Finally, our numerical experiments suggest that the proposed relaxation is strong in that it frequently computes the global optimal solution, together with a proof of global optimality.

Dictionary Learning under Symmetries via Group Representations

The dictionary learning problem can be viewed as a data-driven process to learn a suitable transformation so that data is sparsely represented directly from example data. In this paper, we examine the problem of learning a dictionary that is invariant under a pre-specified group of transformations. Natural settings include Cryo-EM, multi-object tracking, synchronization, pose estimation, etc. We specifically study this problem under the lens of mathematical representation theory. Leveraging the power of non-abelian Fourier analysis for functions over compact groups, we prescribe an algorithmic recipe for learning dictionaries that obey such invariances. We relate the dictionary learning problem in the physical domain, which is naturally modelled as being infinite dimensional, with the associated computational problem, which is necessarily finite dimensional. We establish that the dictionary learning problem can be effectively understood as an optimization instance over certain matrix orbitopes having a particular block-diagonal structure governed by the irreducible representations of the group of symmetries. This perspective enables us to introduce a band-limiting procedure which obtains dimensionality reduction in applications. We provide guarantees for our computational ansatz to provide a desirable dictionary learning outcome. We apply our paradigm to investigate the dictionary learning problem for the groups SO(2) and SO(3). While the SO(2) orbitope admits an exact spectrahedral description, substantially less is understood about the SO(3) orbitope. We describe a tractable spectrahedral outer approximation of the SO(3) orbitope, and contribute an alternating minimization paradigm to perform optimization in this setting. We provide numerical experiments to highlight the efficacy of our approach in learning SO(3) invariant dictionaries, both on synthetic and on real world data.

Optimal Convex and Nonconvex Regularizers for a Data Source

In optimization-based approaches to inverse problems and to statistical estimation, it is common to augment the objective with a regularizer to address challenges associated with ill-posedness. The choice of a suitable regularizer is typically driven by prior domain information and computational considerations. Convex regularizers are attractive as they are endowed with certificates of optimality as well as the toolkit of convex analysis, but exhibit a computational scaling that makes them ill-suited beyond moderate-sized problem instances. On the other hand, nonconvex regularizers can often be deployed at scale, but do not enjoy the certification properties associated with convex regularizers. In this paper, we seek a systematic understanding of the power and the limitations of convex regularization by investigating the following questions: Given a distribution, what are the optimal regularizers, both convex and nonconvex, for data drawn from the distribution? What properties of a data source govern whether it is amenable to convex regularization? We address these questions for the class of continuous and positively homogenous regularizers for which convex and nonconvex regularizers correspond, respectively, to convex bodies and star bodies. By leveraging dual Brunn-Minkowski theory, we show that a radial function derived from a data distribution is the key quantity for identifying optimal regularizers and for assessing the amenability of a data source to convex regularization. Using tools such as $\Gamma$-convergence, we show that our results are robust in the sense that the optimal regularizers for a sample drawn from a distribution converge to their population counterparts as the sample size grows large. Finally, we give generalization guarantees that recover previous results for polyhedral regularizers (i.e., dictionary learning) and lead to new ones for semidefinite regularizers.

Multiplicative updates for symmetric-cone factorizations

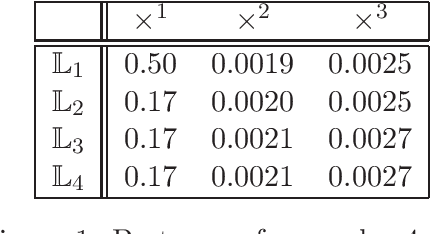
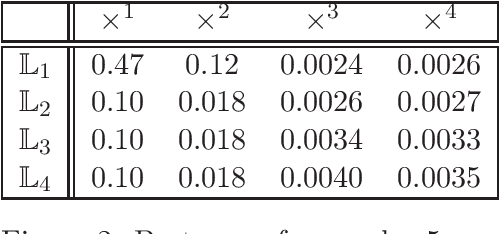
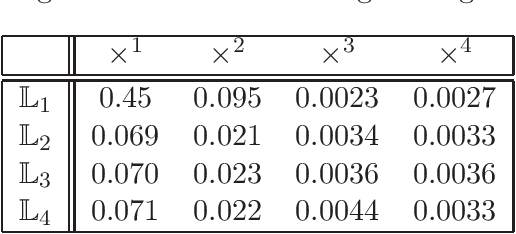
Given a matrix $X\in \mathbb{R}^{m\times n}_+$ with non-negative entries, the cone factorization problem over a cone $\mathcal{K}\subseteq \mathbb{R}^k$ concerns computing $\{ a_1,\ldots, a_{m} \} \subseteq \mathcal{K}$ and $\{ b_1,\ldots, b_{n} \} \subseteq~\mathcal{K}^*$ belonging to its dual so that $X_{ij} = \langle a_i, b_j \rangle$ for all $i\in [m], j\in [n]$. Cone factorizations are fundamental to mathematical optimization as they allow us to express convex bodies as feasible regions of linear conic programs. In this paper, we introduce and analyze the symmetric-cone multiplicative update (SCMU) algorithm for computing cone factorizations when $\mathcal{K}$ is symmetric; i.e., it is self-dual and homogeneous. Symmetric cones are of central interest in mathematical optimization as they provide a common language for studying linear optimization over the nonnegative orthant (linear programs), over the second-order cone (second order cone programs), and over the cone of positive semidefinite matrices (semidefinite programs). The SCMU algorithm is multiplicative in the sense that the iterates are updated by applying a meticulously chosen automorphism of the cone computed using a generalization of the geometric mean to symmetric cones. Using an extension of Lieb's concavity theorem and von Neumann's trace inequality to symmetric cones, we show that the squared loss objective is non-decreasing along the trajectories of the SCMU algorithm. Specialized to the nonnegative orthant, the SCMU algorithm corresponds to the seminal algorithm by Lee and Seung for computing Nonnegative Matrix Factorizations.

A Non-commutative Extension of Lee-Seung's Algorithm for Positive Semidefinite Factorizations

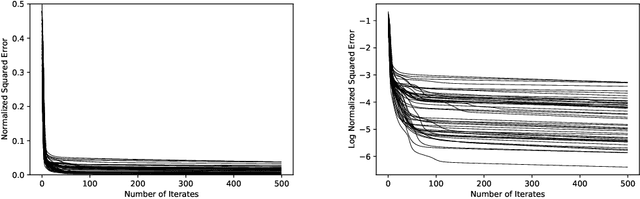
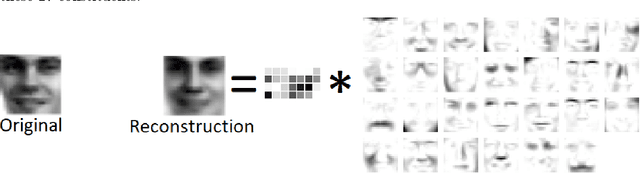
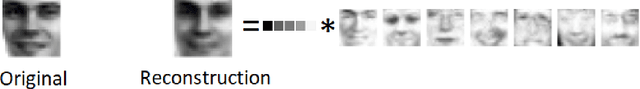
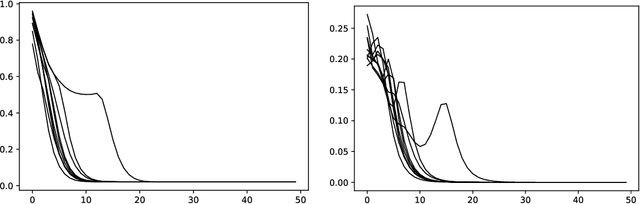
Given a matrix $X\in \mathbb{R}_+^{m\times n}$ with nonnegative entries, a Positive Semidefinite (PSD) factorization of $X$ is a collection of $r \times r$-dimensional PSD matrices $\{A_i\}$ and $\{B_j\}$ satisfying $X_{ij}= \mathrm{tr}(A_i B_j)$ for all $\ i\in [m],\ j\in [n]$. PSD factorizations are fundamentally linked to understanding the expressiveness of semidefinite programs as well as the power and limitations of quantum resources in information theory. The PSD factorization task generalizes the Non-negative Matrix Factorization (NMF) problem where we seek a collection of $r$-dimensional nonnegative vectors $\{a_i\}$ and $\{b_j\}$ satisfying $X_{ij}= a_i^\top b_j$, for all $i\in [m],\ j\in [n]$ -- one can recover the latter problem by choosing matrices in the PSD factorization to be diagonal. The most widely used algorithm for computing NMFs of a matrix is the Multiplicative Update algorithm developed by Lee and Seung, in which nonnegativity of the updates is preserved by scaling with positive diagonal matrices. In this paper, we describe a non-commutative extension of Lee-Seung's algorithm, which we call the Matrix Multiplicative Update (MMU) algorithm, for computing PSD factorizations. The MMU algorithm ensures that updates remain PSD by congruence scaling with the matrix geometric mean of appropriate PSD matrices, and it retains the simplicity of implementation that Lee-Seung's algorithm enjoys. Building on the Majorization-Minimization framework, we show that under our update scheme the squared loss objective is non-increasing and fixed points correspond to critical points. The analysis relies on Lieb's Concavity Theorem. Beyond PSD factorizations, we use the MMU algorithm as a primitive to calculate block-diagonal PSD factorizations and tensor PSD factorizations. We demonstrate the utility of our method with experiments on real and synthetic data.

Group Invariant Dictionary Learning

The dictionary learning problem concerns the task of representing data as sparse linear sums drawn from a smaller collection of basic building blocks. In application domains where such techniques are deployed, we frequently encounter datasets where some form of symmetry or invariance is present. Based on this observation, it is natural to learn dictionaries where such symmetries are also respected. In this paper, we develop a framework for learning dictionaries for data under the constraint that the collection of basic building blocks remains invariant under these symmetries. Our framework specializes to the convolutional dictionary learning problem when we consider translational symmetries. Our procedure for learning such dictionaries relies on representing the symmetry as the action of a matrix group acting on the data, and subsequently introducing a convex penalty function so as to induce sparsity with respect to the collection of matrix group elements. Using properties of positive semidefinite Hermitian Toeplitz matrices, we apply our framework to learn dictionaries that are invariant under continuous shifts. Our numerical experiments on synthetic data and ECG data show that the incorporation of such symmetries as priors are most valuable when the dataset has few data-points, or when the full range of symmetries is inadequately expressed in the dataset.

Collaborative Inference for Efficient Remote Monitoring

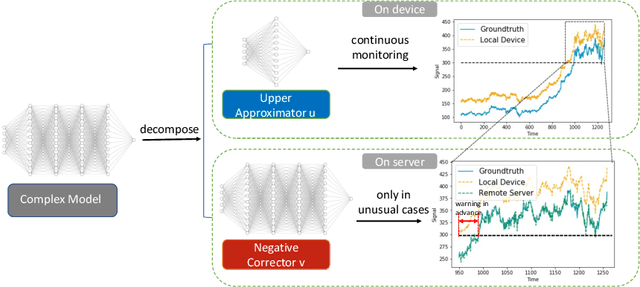
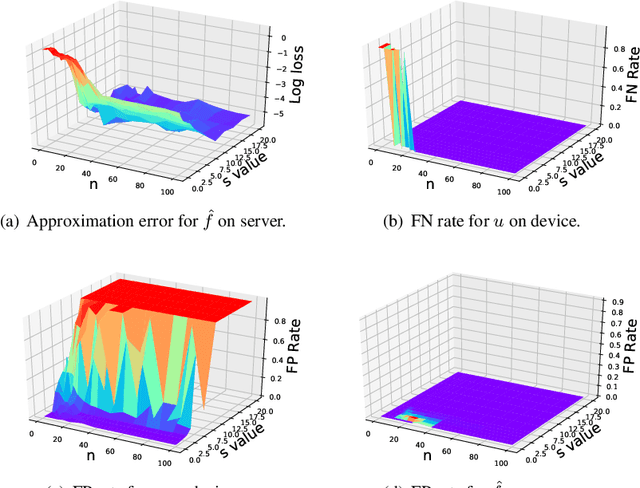
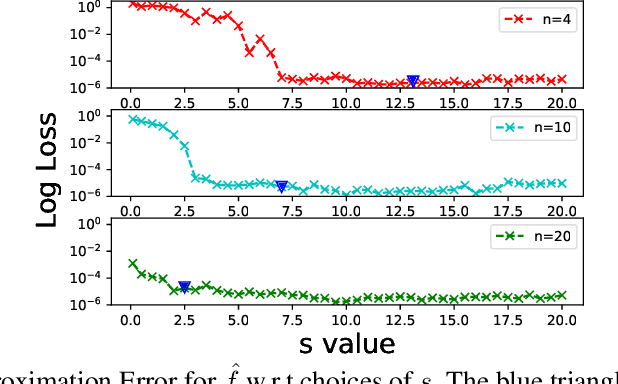
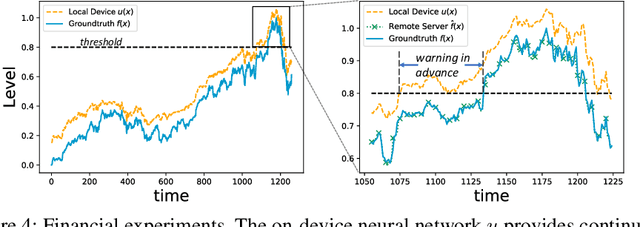
While current machine learning models have impressive performance over a wide range of applications, their large size and complexity render them unsuitable for tasks such as remote monitoring on edge devices with limited storage and computational power. A naive approach to resolve this on the model level is to use simpler architectures, but this sacrifices prediction accuracy and is unsuitable for monitoring applications requiring accurate detection of the onset of adverse events. In this paper, we propose an alternative solution to this problem by decomposing the predictive model as the sum of a simple function which serves as a local monitoring tool, and a complex correction term to be evaluated on the server. A sign requirement is imposed on the latter to ensure that the local monitoring function is safe, in the sense that it can effectively serve as an early warning system. Our analysis quantifies the trade-offs between model complexity and performance, and serves as a guidance for architecture design. We validate our proposed framework on a series of monitoring experiments, where we succeed at learning monitoring models with significantly reduced complexity that minimally violate the safety requirement. More broadly, our framework is useful for learning classifiers in applications where false negatives are significantly more costly compared to false positives.

A Matrix Factorization Approach for Learning Semidefinite-Representable Regularizers

Regularization techniques are widely employed in optimization-based approaches for solving ill-posed inverse problems in data analysis and scientific computing. These methods are based on augmenting the objective with a penalty function, which is specified based on prior domain-specific expertise to induce a desired structure in the solution. We consider the problem of learning suitable regularization functions from data in settings in which precise domain knowledge is not directly available. Previous work under the title of `dictionary learning' or `sparse coding' may be viewed as learning a regularization function that can be computed via linear programming. We describe generalizations of these methods to learn regularizers that can be computed and optimized via semidefinite programming. Our framework for learning such semidefinite regularizers is based on obtaining structured factorizations of data matrices, and our algorithmic approach for computing these factorizations combines recent techniques for rank minimization problems along with an operator analog of Sinkhorn scaling. Under suitable conditions on the input data, our algorithm provides a locally linearly convergent method for identifying the correct regularizer that promotes the type of structure contained in the data. Our analysis is based on the stability properties of Operator Sinkhorn scaling and their relation to geometric aspects of determinantal varieties (in particular tangent spaces with respect to these varieties). The regularizers obtained using our framework can be employed effectively in semidefinite programming relaxations for solving inverse problems.