Discovering How Agents Learn Using Few Data

Decentralized learning algorithms are an essential tool for designing multi-agent systems, as they enable agents to autonomously learn from their experience and past interactions. In this work, we propose a theoretical and algorithmic framework for real-time identification of the learning dynamics that govern agent behavior using a short burst of a single system trajectory. Our method identifies agent dynamics through polynomial regression, where we compensate for limited data by incorporating side-information constraints that capture fundamental assumptions or expectations about agent behavior. These constraints are enforced computationally using sum-of-squares optimization, leading to a hierarchy of increasingly better approximations of the true agent dynamics. Extensive experiments demonstrated that our approach, using only 5 samples from a short run of a single trajectory, accurately recovers the true dynamics across various benchmarks, including equilibrium selection and prediction of chaotic systems up to 10 Lyapunov times. These findings suggest that our approach has significant potential to support effective policy and decision-making in strategic multi-agent systems.

Multiplicative Updates for Online Convex Optimization over Symmetric Cones

We study online convex optimization where the possible actions are trace-one elements in a symmetric cone, generalizing the extensively-studied experts setup and its quantum counterpart. Symmetric cones provide a unifying framework for some of the most important optimization models, including linear, second-order cone, and semidefinite optimization. Using tools from the field of Euclidean Jordan Algebras, we introduce the Symmetric-Cone Multiplicative Weights Update (SCMWU), a projection-free algorithm for online optimization over the trace-one slice of an arbitrary symmetric cone. We show that SCMWU is equivalent to Follow-the-Regularized-Leader and Online Mirror Descent with symmetric-cone negative entropy as regularizer. Using this structural result we show that SCMWU is a no-regret algorithm, and verify our theoretical results with extensive experiments. Our results unify and generalize the analysis for the Multiplicative Weights Update method over the probability simplex and the Matrix Multiplicative Weights Update method over the set of density matrices.

Multiplicative updates for symmetric-cone factorizations

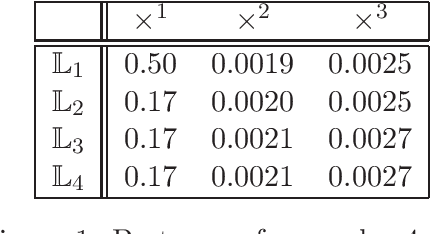
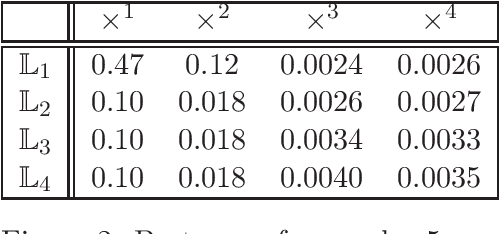
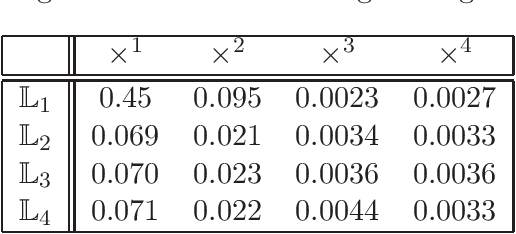
Given a matrix $X\in \mathbb{R}^{m\times n}_+$ with non-negative entries, the cone factorization problem over a cone $\mathcal{K}\subseteq \mathbb{R}^k$ concerns computing $\{ a_1,\ldots, a_{m} \} \subseteq \mathcal{K}$ and $\{ b_1,\ldots, b_{n} \} \subseteq~\mathcal{K}^*$ belonging to its dual so that $X_{ij} = \langle a_i, b_j \rangle$ for all $i\in [m], j\in [n]$. Cone factorizations are fundamental to mathematical optimization as they allow us to express convex bodies as feasible regions of linear conic programs. In this paper, we introduce and analyze the symmetric-cone multiplicative update (SCMU) algorithm for computing cone factorizations when $\mathcal{K}$ is symmetric; i.e., it is self-dual and homogeneous. Symmetric cones are of central interest in mathematical optimization as they provide a common language for studying linear optimization over the nonnegative orthant (linear programs), over the second-order cone (second order cone programs), and over the cone of positive semidefinite matrices (semidefinite programs). The SCMU algorithm is multiplicative in the sense that the iterates are updated by applying a meticulously chosen automorphism of the cone computed using a generalization of the geometric mean to symmetric cones. Using an extension of Lieb's concavity theorem and von Neumann's trace inequality to symmetric cones, we show that the squared loss objective is non-decreasing along the trajectories of the SCMU algorithm. Specialized to the nonnegative orthant, the SCMU algorithm corresponds to the seminal algorithm by Lee and Seung for computing Nonnegative Matrix Factorizations.

A Non-commutative Extension of Lee-Seung's Algorithm for Positive Semidefinite Factorizations

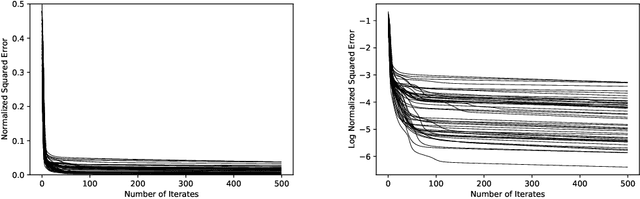
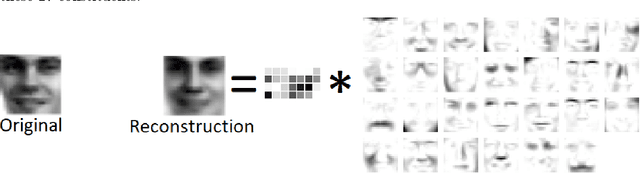
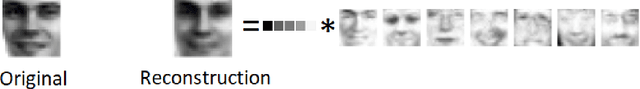
Given a matrix $X\in \mathbb{R}_+^{m\times n}$ with nonnegative entries, a Positive Semidefinite (PSD) factorization of $X$ is a collection of $r \times r$-dimensional PSD matrices $\{A_i\}$ and $\{B_j\}$ satisfying $X_{ij}= \mathrm{tr}(A_i B_j)$ for all $\ i\in [m],\ j\in [n]$. PSD factorizations are fundamentally linked to understanding the expressiveness of semidefinite programs as well as the power and limitations of quantum resources in information theory. The PSD factorization task generalizes the Non-negative Matrix Factorization (NMF) problem where we seek a collection of $r$-dimensional nonnegative vectors $\{a_i\}$ and $\{b_j\}$ satisfying $X_{ij}= a_i^\top b_j$, for all $i\in [m],\ j\in [n]$ -- one can recover the latter problem by choosing matrices in the PSD factorization to be diagonal. The most widely used algorithm for computing NMFs of a matrix is the Multiplicative Update algorithm developed by Lee and Seung, in which nonnegativity of the updates is preserved by scaling with positive diagonal matrices. In this paper, we describe a non-commutative extension of Lee-Seung's algorithm, which we call the Matrix Multiplicative Update (MMU) algorithm, for computing PSD factorizations. The MMU algorithm ensures that updates remain PSD by congruence scaling with the matrix geometric mean of appropriate PSD matrices, and it retains the simplicity of implementation that Lee-Seung's algorithm enjoys. Building on the Majorization-Minimization framework, we show that under our update scheme the squared loss objective is non-increasing and fixed points correspond to critical points. The analysis relies on Lieb's Concavity Theorem. Beyond PSD factorizations, we use the MMU algorithm as a primitive to calculate block-diagonal PSD factorizations and tensor PSD factorizations. We demonstrate the utility of our method with experiments on real and synthetic data.

Convergence to Second-Order Stationarity for Non-negative Matrix Factorization: Provably and Concurrently

Non-negative matrix factorization (NMF) is a fundamental non-convex optimization problem with numerous applications in Machine Learning (music analysis, document clustering, speech-source separation etc). Despite having received extensive study, it is poorly understood whether or not there exist natural algorithms that can provably converge to a local minimum. Part of the reason is because the objective is heavily symmetric and its gradient is not Lipschitz. In this paper we define a multiplicative weight update type dynamics (modification of the seminal Lee-Seung algorithm) that runs concurrently and provably avoids saddle points (first order stationary points that are not second order). Our techniques combine tools from dynamical systems such as stability and exploit the geometry of the NMF objective by reducing the standard NMF formulation over the non-negative orthant to a new formulation over (a scaled) simplex. An important advantage of our method is the use of concurrent updates, which permits implementations in parallel computing environments.

Analysis of Optimization Algorithms via Sum-of-Squares

In this work, we introduce a new framework for unifying and systematizing the performance analysis of first-order black-box optimization algorithms for unconstrained convex minimization over finite-dimensional Euclidean spaces. The low-cost iteration complexity enjoyed by this class of algorithms renders them particularly relevant for applications in machine learning and large-scale data analysis. However, existing proofs of convergence of such optimization algorithms consist mostly of ad-hoc arguments and case-by-case analyses. On the other hand, our approach is based on sum-of-squares optimization and puts forward a promising framework for unifying the convergence {analyses} of optimization algorithms. Illustrating the usefulness of our approach, we recover several known convergence bounds for four widely-used first-order algorithms in a unified manner, and also derive one new convergence result for gradient descent with Armijo-terminated line search.