A Non-commutative Extension of Lee-Seung's Algorithm for Positive Semidefinite Factorizations

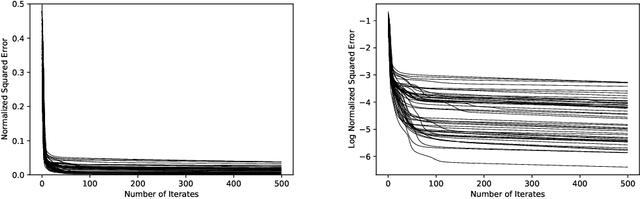
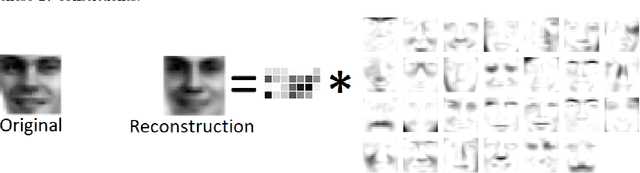
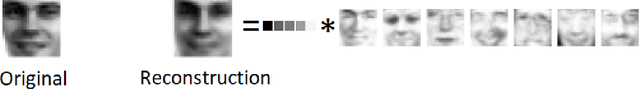
Given a matrix $X\in \mathbb{R}_+^{m\times n}$ with nonnegative entries, a Positive Semidefinite (PSD) factorization of $X$ is a collection of $r \times r$-dimensional PSD matrices $\{A_i\}$ and $\{B_j\}$ satisfying $X_{ij}= \mathrm{tr}(A_i B_j)$ for all $\ i\in [m],\ j\in [n]$. PSD factorizations are fundamentally linked to understanding the expressiveness of semidefinite programs as well as the power and limitations of quantum resources in information theory. The PSD factorization task generalizes the Non-negative Matrix Factorization (NMF) problem where we seek a collection of $r$-dimensional nonnegative vectors $\{a_i\}$ and $\{b_j\}$ satisfying $X_{ij}= a_i^\top b_j$, for all $i\in [m],\ j\in [n]$ -- one can recover the latter problem by choosing matrices in the PSD factorization to be diagonal. The most widely used algorithm for computing NMFs of a matrix is the Multiplicative Update algorithm developed by Lee and Seung, in which nonnegativity of the updates is preserved by scaling with positive diagonal matrices. In this paper, we describe a non-commutative extension of Lee-Seung's algorithm, which we call the Matrix Multiplicative Update (MMU) algorithm, for computing PSD factorizations. The MMU algorithm ensures that updates remain PSD by congruence scaling with the matrix geometric mean of appropriate PSD matrices, and it retains the simplicity of implementation that Lee-Seung's algorithm enjoys. Building on the Majorization-Minimization framework, we show that under our update scheme the squared loss objective is non-increasing and fixed points correspond to critical points. The analysis relies on Lieb's Concavity Theorem. Beyond PSD factorizations, we use the MMU algorithm as a primitive to calculate block-diagonal PSD factorizations and tensor PSD factorizations. We demonstrate the utility of our method with experiments on real and synthetic data.