Multiplicative updates for symmetric-cone factorizations
Paper and Code
Aug 02, 2021
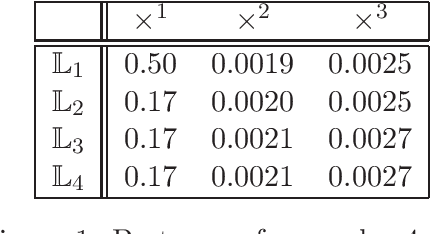
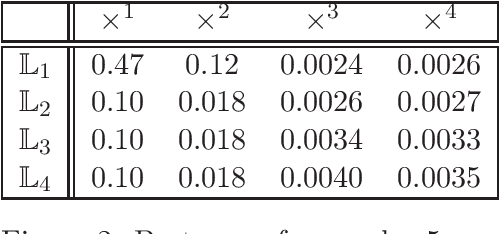
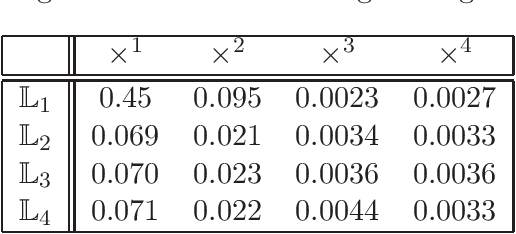
Given a matrix $X\in \mathbb{R}^{m\times n}_+$ with non-negative entries, the cone factorization problem over a cone $\mathcal{K}\subseteq \mathbb{R}^k$ concerns computing $\{ a_1,\ldots, a_{m} \} \subseteq \mathcal{K}$ and $\{ b_1,\ldots, b_{n} \} \subseteq~\mathcal{K}^*$ belonging to its dual so that $X_{ij} = \langle a_i, b_j \rangle$ for all $i\in [m], j\in [n]$. Cone factorizations are fundamental to mathematical optimization as they allow us to express convex bodies as feasible regions of linear conic programs. In this paper, we introduce and analyze the symmetric-cone multiplicative update (SCMU) algorithm for computing cone factorizations when $\mathcal{K}$ is symmetric; i.e., it is self-dual and homogeneous. Symmetric cones are of central interest in mathematical optimization as they provide a common language for studying linear optimization over the nonnegative orthant (linear programs), over the second-order cone (second order cone programs), and over the cone of positive semidefinite matrices (semidefinite programs). The SCMU algorithm is multiplicative in the sense that the iterates are updated by applying a meticulously chosen automorphism of the cone computed using a generalization of the geometric mean to symmetric cones. Using an extension of Lieb's concavity theorem and von Neumann's trace inequality to symmetric cones, we show that the squared loss objective is non-decreasing along the trajectories of the SCMU algorithm. Specialized to the nonnegative orthant, the SCMU algorithm corresponds to the seminal algorithm by Lee and Seung for computing Nonnegative Matrix Factorizations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge