Last-iterate Convergence Separation between Extra-gradient and Optimism in Constrained Periodic Games

Last-iterate behaviors of learning algorithms in repeated two-player zero-sum games have been extensively studied due to their wide applications in machine learning and related tasks. Typical algorithms that exhibit the last-iterate convergence property include optimistic and extra-gradient methods. However, most existing results establish these properties under the assumption that the game is time-independent. Recently, (Feng et al, 2023) studied the last-iterate behaviors of optimistic and extra-gradient methods in games with a time-varying payoff matrix, and proved that in an unconstrained periodic game, extra-gradient method converges to the equilibrium while optimistic method diverges. This finding challenges the conventional wisdom that these two methods are expected to behave similarly as they do in time-independent games. However, compared to unconstrained games, games with constrains are more common both in practical and theoretical studies. In this paper, we investigate the last-iterate behaviors of optimistic and extra-gradient methods in the constrained periodic games, demonstrating that similar separation results for last-iterate convergence also hold in this setting.

Optimistic Policy Gradient in Multi-Player Markov Games with a Single Controller: Convergence Beyond the Minty Property

Policy gradient methods enjoy strong practical performance in numerous tasks in reinforcement learning. Their theoretical understanding in multiagent settings, however, remains limited, especially beyond two-player competitive and potential Markov games. In this paper, we develop a new framework to characterize optimistic policy gradient methods in multi-player Markov games with a single controller. Specifically, under the further assumption that the game exhibits an equilibrium collapse, in that the marginals of coarse correlated equilibria (CCE) induce Nash equilibria (NE), we show convergence to stationary $\epsilon$-NE in $O(1/\epsilon^2)$ iterations, where $O(\cdot)$ suppresses polynomial factors in the natural parameters of the game. Such an equilibrium collapse is well-known to manifest itself in two-player zero-sum Markov games, but also occurs even in a class of multi-player Markov games with separable interactions, as established by recent work. As a result, we bypass known complexity barriers for computing stationary NE when either of our assumptions fails. Our approach relies on a natural generalization of the classical Minty property that we introduce, which we anticipate to have further applications beyond Markov games.

On the Convergence of No-Regret Learning Dynamics in Time-Varying Games

Most of the literature on learning in games has focused on the restrictive setting where the underlying repeated game does not change over time. Much less is known about the convergence of no-regret learning algorithms in dynamic multiagent settings. In this paper, we characterize the convergence of \emph{optimistic gradient descent (OGD)} in time-varying games by drawing a strong connection with \emph{dynamic regret}. Our framework yields sharp convergence bounds for the equilibrium gap of OGD in zero-sum games parameterized on the \emph{minimal} first-order variation of the Nash equilibria and the second-order variation of the payoff matrices, subsuming known results for static games. Furthermore, we establish improved \emph{second-order} variation bounds under strong convexity-concavity, as long as each game is repeated multiple times. Our results also apply to time-varying \emph{general-sum} multi-player games via a bilinear formulation of correlated equilibria, which has novel implications for meta-learning and for obtaining refined variation-dependent regret bounds, addressing questions left open in prior papers. Finally, we leverage our framework to also provide new insights on dynamic regret guarantees in static games.

On Scrambling Phenomena for Randomly Initialized Recurrent Networks

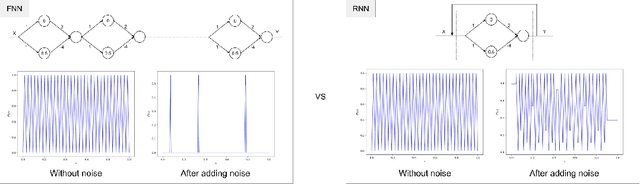
Recurrent Neural Networks (RNNs) frequently exhibit complicated dynamics, and their sensitivity to the initialization process often renders them notoriously hard to train. Recent works have shed light on such phenomena analyzing when exploding or vanishing gradients may occur, either of which is detrimental for training dynamics. In this paper, we point to a formal connection between RNNs and chaotic dynamical systems and prove a qualitatively stronger phenomenon about RNNs than what exploding gradients seem to suggest. Our main result proves that under standard initialization (e.g., He, Xavier etc.), RNNs will exhibit \textit{Li-Yorke chaos} with \textit{constant} probability \textit{independent} of the network's width. This explains the experimentally observed phenomenon of \textit{scrambling}, under which trajectories of nearby points may appear to be arbitrarily close during some timesteps, yet will be far away in future timesteps. In stark contrast to their feedforward counterparts, we show that chaotic behavior in RNNs is preserved under small perturbations and that their expressive power remains exponential in the number of feedback iterations. Our technical arguments rely on viewing RNNs as random walks under non-linear activations, and studying the existence of certain types of higher-order fixed points called \textit{periodic points} that lead to phase transitions from order to chaos.

Efficiently Computing Nash Equilibria in Adversarial Team Markov Games

Computing Nash equilibrium policies is a central problem in multi-agent reinforcement learning that has received extensive attention both in theory and in practice. However, provable guarantees have been thus far either limited to fully competitive or cooperative scenarios or impose strong assumptions that are difficult to meet in most practical applications. In this work, we depart from those prior results by investigating infinite-horizon \emph{adversarial team Markov games}, a natural and well-motivated class of games in which a team of identically-interested players -- in the absence of any explicit coordination or communication -- is competing against an adversarial player. This setting allows for a unifying treatment of zero-sum Markov games and Markov potential games, and serves as a step to model more realistic strategic interactions that feature both competing and cooperative interests. Our main contribution is the first algorithm for computing stationary $\epsilon$-approximate Nash equilibria in adversarial team Markov games with computational complexity that is polynomial in all the natural parameters of the game, as well as $1/\epsilon$. The proposed algorithm is particularly natural and practical, and it is based on performing independent policy gradient steps for each player in the team, in tandem with best responses from the side of the adversary; in turn, the policy for the adversary is then obtained by solving a carefully constructed linear program. Our analysis leverages non-standard techniques to establish the KKT optimality conditions for a nonlinear program with nonconvex constraints, thereby leading to a natural interpretation of the induced Lagrange multipliers. Along the way, we significantly extend an important characterization of optimal policies in adversarial (normal-form) team games due to Von Stengel and Koller (GEB `97).

Accelerated Multiplicative Weights Update Avoids Saddle Points almost always

We consider non-convex optimization problems with constraint that is a product of simplices. A commonly used algorithm in solving this type of problem is the Multiplicative Weights Update (MWU), an algorithm that is widely used in game theory, machine learning and multi-agent systems. Despite it has been known that MWU avoids saddle points, there is a question that remains unaddressed:"Is there an accelerated version of MWU that avoids saddle points provably?" In this paper we provide a positive answer to above question. We provide an accelerated MWU based on Riemannian Accelerated Gradient Descent, and prove that the Riemannian Accelerated Gradient Descent, thus the accelerated MWU, almost always avoid saddle points.

Teamwork makes von Neumann work: Min-Max Optimization in Two-Team Zero-Sum Games

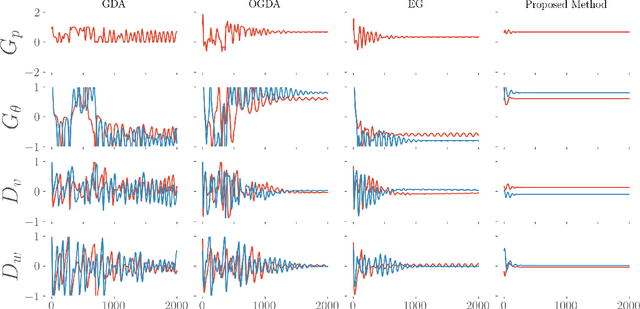
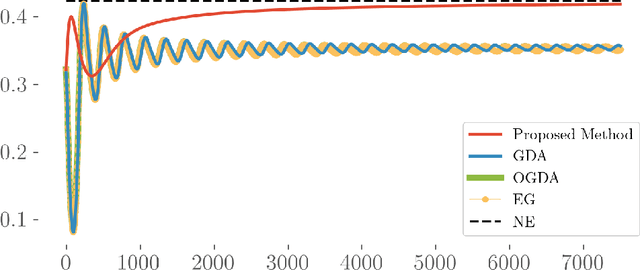
Motivated by recent advances in both theoretical and applied aspects of multiplayer games, spanning from e-sports to multi-agent generative adversarial networks, we focus on min-max optimization in team zero-sum games. In this class of games, players are split into two teams with payoffs equal within the same team and of opposite sign across the opponent team. Unlike the textbook two-player zero-sum games, finding a Nash equilibrium in our class can be shown to be CLS-hard, i.e., it is unlikely to have a polynomial-time algorithm for computing Nash equilibria. Moreover, in this generalized framework, we establish that even asymptotic last iterate or time average convergence to a Nash Equilibrium is not possible using Gradient Descent Ascent (GDA), its optimistic variant, and extra gradient. Specifically, we present a family of team games whose induced utility is \emph{non} multi-linear with \emph{non} attractive \emph{per-se} mixed Nash Equilibria, as strict saddle points of the underlying optimization landscape. Leveraging techniques from control theory, we complement these negative results by designing a modified GDA that converges locally to Nash equilibria. Finally, we discuss connections of our framework with AI architectures with team competition structures like multi-agent generative adversarial networks.

Independent Natural Policy Gradient Always Converges in Markov Potential Games

Multi-agent reinforcement learning has been successfully applied to fully-cooperative and fully-competitive environments, but little is currently known about mixed cooperative/competitive environments. In this paper, we focus on a particular class of multi-agent mixed cooperative/competitive stochastic games called Markov Potential Games (MPGs), which include cooperative games as a special case. Recent results have shown that independent policy gradient converges in MPGs but it was not known whether Independent Natural Policy Gradient converges in MPGs as well. We prove that Independent Natural Policy Gradient always converges in the last iterate using constant learning rates. The proof deviates from the existing approaches and the main challenge lies in the fact that Markov Potential Games do not have unique optimal values (as single-agent settings exhibit) so different initializations can lead to different limit point values. We complement our theoretical results with experiments that indicate that Natural Policy Gradient outperforms Policy Gradient in routing games and congestion games.

Global Convergence of Multi-Agent Policy Gradient in Markov Potential Games

Potential games are arguably one of the most important and widely studied classes of normal form games. They define the archetypal setting of multi-agent coordination as all agent utilities are perfectly aligned with each other via a common potential function. Can this intuitive framework be transplanted in the setting of Markov Games? What are the similarities and differences between multi-agent coordination with and without state dependence? We present a novel definition of Markov Potential Games (MPG) that generalizes prior attempts at capturing complex stateful multi-agent coordination. Counter-intuitively, insights from normal-form potential games do not carry over as MPGs can consist of settings where state-games can be zero-sum games. In the opposite direction, Markov games where every state-game is a potential game are not necessarily MPGs. Nevertheless, MPGs showcase standard desirable properties such as the existence of deterministic Nash policies. In our main technical result, we prove fast convergence of independent policy gradient to Nash policies by adapting recent gradient dominance property arguments developed for single agent MDPs to multi-agent learning settings.

Fast Convergence of Langevin Dynamics on Manifold: Geodesics meet Log-Sobolev

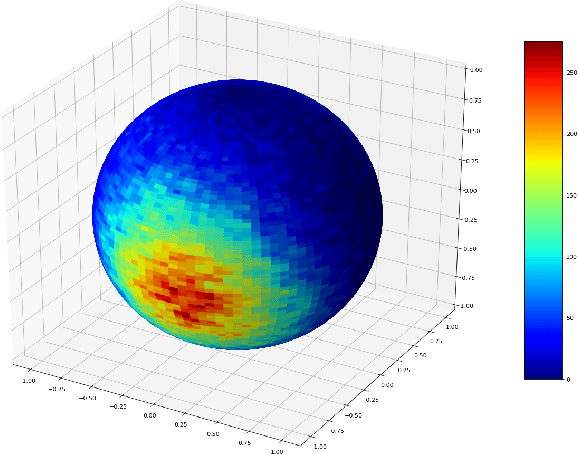
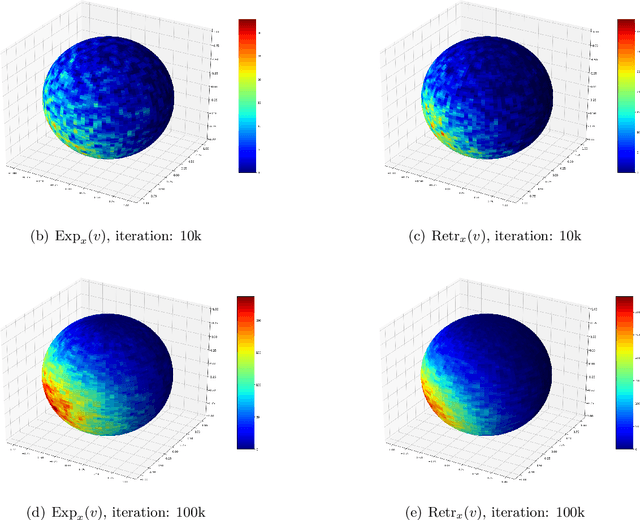
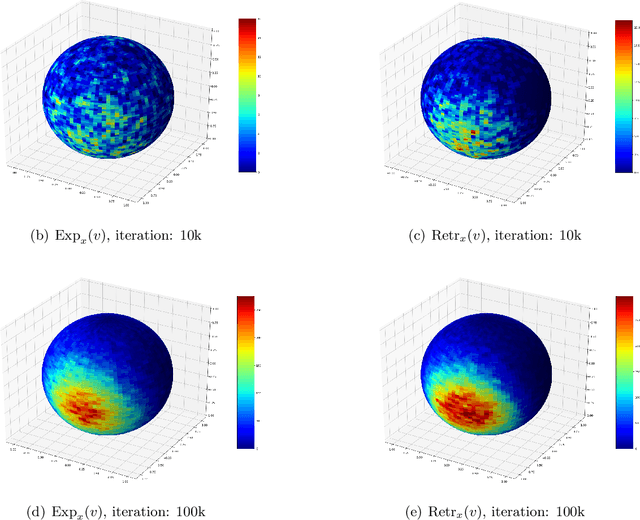
Sampling is a fundamental and arguably very important task with numerous applications in Machine Learning. One approach to sample from a high dimensional distribution $e^{-f}$ for some function $f$ is the Langevin Algorithm (LA). Recently, there has been a lot of progress in showing fast convergence of LA even in cases where $f$ is non-convex, notably [53], [39] in which the former paper focuses on functions $f$ defined in $\mathbb{R}^n$ and the latter paper focuses on functions with symmetries (like matrix completion type objectives) with manifold structure. Our work generalizes the results of [53] where $f$ is defined on a manifold $M$ rather than $\mathbb{R}^n$. From technical point of view, we show that KL decreases in a geometric rate whenever the distribution $e^{-f}$ satisfies a log-Sobolev inequality on $M$.