adaPARL: Adaptive Privacy-Aware Reinforcement Learning for Sequential-Decision Making Human-in-the-Loop Systems

Reinforcement learning (RL) presents numerous benefits compared to rule-based approaches in various applications. Privacy concerns have grown with the widespread use of RL trained with privacy-sensitive data in IoT devices, especially for human-in-the-loop systems. On the one hand, RL methods enhance the user experience by trying to adapt to the highly dynamic nature of humans. On the other hand, trained policies can leak the user's private information. Recent attention has been drawn to designing privacy-aware RL algorithms while maintaining an acceptable system utility. A central challenge in designing privacy-aware RL, especially for human-in-the-loop systems, is that humans have intrinsic variability and their preferences and behavior evolve. The effect of one privacy leak mitigation can be different for the same human or across different humans over time. Hence, we can not design one fixed model for privacy-aware RL that fits all. To that end, we propose adaPARL, an adaptive approach for privacy-aware RL, especially for human-in-the-loop IoT systems. adaPARL provides a personalized privacy-utility trade-off depending on human behavior and preference. We validate the proposed adaPARL on two IoT applications, namely (i) Human-in-the-Loop Smart Home and (ii) Human-in-the-Loop Virtual Reality (VR) Smart Classroom. Results obtained on these two applications validate the generality of adaPARL and its ability to provide a personalized privacy-utility trade-off. On average, for the first application, adaPARL improves the utility by $57\%$ over the baseline and by $43\%$ over randomization. adaPARL also reduces the privacy leak by $23\%$ on average. For the second application, adaPARL decreases the privacy leak to $44\%$ before the utility drops by $15\%$.

On Scrambling Phenomena for Randomly Initialized Recurrent Networks

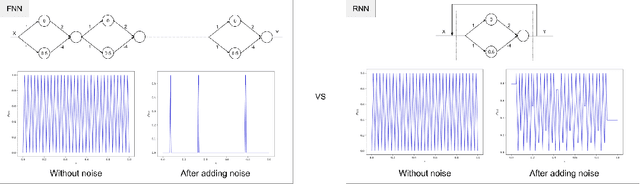
Recurrent Neural Networks (RNNs) frequently exhibit complicated dynamics, and their sensitivity to the initialization process often renders them notoriously hard to train. Recent works have shed light on such phenomena analyzing when exploding or vanishing gradients may occur, either of which is detrimental for training dynamics. In this paper, we point to a formal connection between RNNs and chaotic dynamical systems and prove a qualitatively stronger phenomenon about RNNs than what exploding gradients seem to suggest. Our main result proves that under standard initialization (e.g., He, Xavier etc.), RNNs will exhibit \textit{Li-Yorke chaos} with \textit{constant} probability \textit{independent} of the network's width. This explains the experimentally observed phenomenon of \textit{scrambling}, under which trajectories of nearby points may appear to be arbitrarily close during some timesteps, yet will be far away in future timesteps. In stark contrast to their feedforward counterparts, we show that chaotic behavior in RNNs is preserved under small perturbations and that their expressive power remains exponential in the number of feedback iterations. Our technical arguments rely on viewing RNNs as random walks under non-linear activations, and studying the existence of certain types of higher-order fixed points called \textit{periodic points} that lead to phase transitions from order to chaos.