Near-Optimal Dynamic Matching via Coarsening with Application to Heart Transplantation

Online matching has been a mainstay in domains such as Internet advertising and organ allocation, but practical algorithms often lack strong theoretical guarantees. We take an important step toward addressing this by developing new online matching algorithms based on a coarsening approach. Although coarsening typically implies a loss of granularity, we show that, to the contrary, aggregating offline nodes into capacitated clusters can yield near-optimal theoretical guarantees. We apply our methodology to heart transplant allocation to develop theoretically grounded policies based on structural properties of historical data. In realistic simulations, our policy closely matches the performance of the omniscient benchmark. Our work bridges the gap between data-driven heuristics and pessimistic theoretical lower bounds, and provides rigorous justification for prior clustering-based approaches in organ allocation.

Position: Machine Learning for Heart Transplant Allocation Policy Optimization Should Account for Incentives

The allocation of scarce donor organs constitutes one of the most consequential algorithmic challenges in healthcare. While the field is rapidly transitioning from rigid, rule-based systems to machine learning and data-driven optimization, we argue that current approaches often overlook a fundamental barrier: incentives. In this position paper, we highlight that organ allocation is not merely a static optimization problem, but rather a complex game involving transplant centers, clinicians, and regulators. Focusing on US adult heart transplant allocation, we identify critical incentive misalignments across the decision-making pipeline, and present data showing that they are having adverse consequences today. Our main position is that the next generation of allocation policies should be incentive aware. We outline a research agenda for the machine learning community, calling for the integration of mechanism design, strategic classification, causal inference, and social choice to ensure robustness, efficiency, and fairness in the face of strategic behavior from the various constituent groups.

Policy Optimization for Dynamic Heart Transplant Allocation

Heart transplantation is a viable path for patients suffering from advanced heart failure, but this lifesaving option is severely limited due to donor shortage. Although the current allocation policy was recently revised in 2018, a major concern is that it does not adequately take into account pretransplant and post-transplant mortality. In this paper, we take an important step toward addressing these deficiencies. To begin with, we use historical data from UNOS to develop a new simulator that enables us to evaluate and compare the performance of different policies. We then leverage our simulator to demonstrate that the status quo policy is considerably inferior to the myopic policy that matches incoming donors to the patient who maximizes the number of years gained by the transplant. Moreover, we develop improved policies that account for the dynamic nature of the allocation process through the use of potentials -- a measure of a patient's utility in future allocations that we introduce. We also show that batching together even a handful of donors -- which is a viable option for a certain type of donors -- further enhances performance. Our simulator also allows us to evaluate the effect of critical, and often unexplored, factors in the allocation, such as geographic proximity and the tendency to reject offers by the transplant centers.

Scale-Invariant Regret Matching and Online Learning with Optimal Convergence: Bridging Theory and Practice in Zero-Sum Games

A considerable chasm has been looming for decades between theory and practice in zero-sum game solving through first-order methods. Although a convergence rate of $T^{-1}$ has long been established since Nemirovski's mirror-prox algorithm and Nesterov's excessive gap technique in the early 2000s, the most effective paradigm in practice is *counterfactual regret minimization*, which is based on *regret matching* and its modern variants. In particular, the state of the art across most benchmarks is *predictive* regret matching$^+$ (PRM$^+$), in conjunction with non-uniform averaging. Yet, such algorithms can exhibit slower $\Omega(T^{-1/2})$ convergence even in self-play. In this paper, we close the gap between theory and practice. We propose a new scale-invariant and parameter-free variant of PRM$^+$, which we call IREG-PRM$^+$. We show that it achieves $T^{-1/2}$ best-iterate and $T^{-1}$ (i.e., optimal) average-iterate convergence guarantees, while also being on par with PRM$^+$ on benchmark games. From a technical standpoint, we draw an analogy between IREG-PRM$^+$ and optimistic gradient descent with *adaptive* learning rate. The basic flaw of PRM$^+$ is that the ($\ell_2$-)norm of the regret vector -- which can be thought of as the inverse of the learning rate -- can decrease. By contrast, we design IREG-PRM$^+$ so as to maintain the invariance that the norm of the regret vector is nondecreasing. This enables us to derive an RVU-type bound for IREG-PRM$^+$, the first such property that does not rely on introducing additional hyperparameters to enforce smoothness. Furthermore, we find that IREG-PRM$^+$ performs on par with an adaptive version of optimistic gradient descent that we introduce whose learning rate depends on the misprediction error, demystifying the effectiveness of the regret matching family *vis-a-vis* more standard optimization techniques.

A Polynomial-Time Algorithm for Variational Inequalities under the Minty Condition

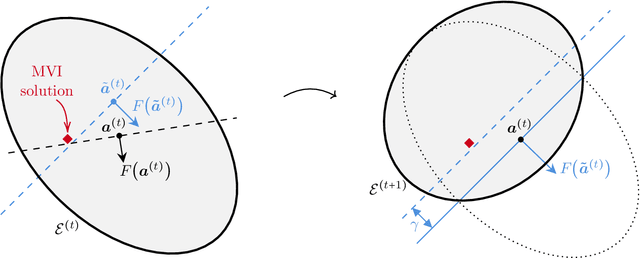
Solving (Stampacchia) variational inequalities (SVIs) is a foundational problem at the heart of optimization, with a host of critical applications ranging from engineering to economics. However, this expressivity comes at the cost of computational hardness. As a result, most research has focused on carving out specific subclasses that elude those intractability barriers. A classical property that goes back to the 1960s is the Minty condition, which postulates that the Minty VI (MVI) problem -- the weak dual of the SVI problem -- admits a solution. In this paper, we establish the first polynomial-time algorithm -- that is, with complexity growing polynomially in the dimension $d$ and $\log(1/\epsilon)$ -- for solving $\epsilon$-SVIs for Lipschitz continuous mappings under the Minty condition. Prior approaches either incurred an exponentially worse dependence on $1/\epsilon$ (and other natural parameters of the problem) or made overly restrictive assumptions -- such as strong monotonicity. To do so, we introduce a new variant of the ellipsoid algorithm wherein separating hyperplanes are obtained after taking a gradient descent step from the center of the ellipsoid. It succeeds even though the set of SVIs can be nonconvex and not fully dimensional. Moreover, when our algorithm is applied to an instance with no MVI solution and fails to identify an SVI solution, it produces a succinct certificate of MVI infeasibility. We also show that deciding whether the Minty condition holds is $\mathsf{coNP}$-complete. We provide several extensions and new applications of our main results. Specifically, we obtain the first polynomial-time algorithms for i) solving monotone VIs, ii) globally minimizing a (potentially nonsmooth) quasar-convex function, and iii) computing Nash equilibria in multi-player harmonic games.

Learning and Computation of $Φ$-Equilibria at the Frontier of Tractability

$\Phi$-equilibria -- and the associated notion of $\Phi$-regret -- are a powerful and flexible framework at the heart of online learning and game theory, whereby enriching the set of deviations $\Phi$ begets stronger notions of rationality. Recently, Daskalakis, Farina, Fishelson, Pipis, and Schneider (STOC '24) -- abbreviated as DFFPS -- settled the existence of efficient algorithms when $\Phi$ contains only linear maps under a general, $d$-dimensional convex constraint set $\mathcal{X}$. In this paper, we significantly extend their work by resolving the case where $\Phi$ is $k$-dimensional; degree-$\ell$ polynomials constitute a canonical such example with $k = d^{O(\ell)}$. In particular, positing only oracle access to $\mathcal{X}$, we obtain two main positive results: i) a $\text{poly}(n, d, k, \text{log}(1/\epsilon))$-time algorithm for computing $\epsilon$-approximate $\Phi$-equilibria in $n$-player multilinear games, and ii) an efficient online algorithm that incurs average $\Phi$-regret at most $\epsilon$ using $\text{poly}(d, k)/\epsilon^2$ rounds. We also show nearly matching lower bounds in the online learning setting, thereby obtaining for the first time a family of deviations that captures the learnability of $\Phi$-regret. From a technical standpoint, we extend the framework of DFFPS from linear maps to the more challenging case of maps with polynomial dimension. At the heart of our approach is a polynomial-time algorithm for computing an expected fixed point of any $\phi : \mathcal{X} \to \mathcal{X}$ based on the ellipsoid against hope (EAH) algorithm of Papadimitriou and Roughgarden (JACM '08). In particular, our algorithm for computing $\Phi$-equilibria is based on executing EAH in a nested fashion -- each step of EAH itself being implemented by invoking a separate call to EAH.

Expected Variational Inequalities

Variational inequalities (VIs) encompass many fundamental problems in diverse areas ranging from engineering to economics and machine learning. However, their considerable expressivity comes at the cost of computational intractability. In this paper, we introduce and analyze a natural relaxation -- which we refer to as expected variational inequalities (EVIs) -- where the goal is to find a distribution that satisfies the VI constraint in expectation. By adapting recent techniques from game theory, we show that, unlike VIs, EVIs can be solved in polynomial time under general (nonmonotone) operators. EVIs capture the seminal notion of correlated equilibria, but enjoy a greater reach beyond games. We also employ our framework to capture and generalize several existing disparate results, including from settings such as smooth games, and games with coupled constraints or nonconcave utilities.

Barriers to Welfare Maximization with No-Regret Learning

A celebrated result in the interface of online learning and game theory guarantees that the repeated interaction of no-regret players leads to a coarse correlated equilibrium (CCE) -- a natural game-theoretic solution concept. Despite the rich history of this foundational problem and the tremendous interest it has received in recent years, a basic question still remains open: how many iterations are needed for no-regret players to approximate an equilibrium? In this paper, we establish the first computational lower bounds for that problem in two-player (general-sum) games under the constraint that the CCE reached approximates the optimal social welfare (or some other natural objective). From a technical standpoint, our approach revolves around proving lower bounds for computing a near-optimal $T$-sparse CCE -- a mixture of $T$ product distributions, thereby circumscribing the iteration complexity of no-regret learning even in the centralized model of computation. Our proof proceeds by extending a classical reduction of Gilboa and Zemel [1989] for optimal Nash to sparse (approximate) CCE. In particular, we show that the inapproximability of maximum clique precludes attaining any non-trivial sparsity in polynomial time. Moreover, we strengthen our hardness results to apply in the low-precision regime as well via the planted clique conjecture.

Computational Lower Bounds for Regret Minimization in Normal-Form Games

A celebrated connection in the interface of online learning and game theory establishes that players minimizing swap regret converge to correlated equilibria (CE) -- a seminal game-theoretic solution concept. Despite the long history of this problem and the renewed interest it has received in recent years, a basic question remains open: how many iterations are needed to approximate an equilibrium under the usual normal-form representation? In this paper, we provide evidence that existing learning algorithms, such as multiplicative weights update, are close to optimal. In particular, we prove lower bounds for the problem of computing a CE that can be expressed as a uniform mixture of $T$ product distributions -- namely, a uniform $T$-sparse CE; such lower bounds immediately circumscribe (computationally bounded) regret minimization algorithms in games. Our results are obtained in the algorithmic framework put forward by Kothari and Mehta (STOC 2018) in the context of computing Nash equilibria, which consists of the sum-of-squares (SoS) relaxation in conjunction with oracle access to a verification oracle; the goal in that framework is to lower bound either the degree of the SoS relaxation or the number of queries to the verification oracle. Here, we obtain two such hardness results, precluding computing i) uniform $\text{log }n$-sparse CE when $\epsilon =\text{poly}(1/\text{log }n)$ and ii) uniform $n^{1 - o(1)}$-sparse CE when $\epsilon = \text{poly}(1/n)$.

Optimistic Policy Gradient in Multi-Player Markov Games with a Single Controller: Convergence Beyond the Minty Property

Policy gradient methods enjoy strong practical performance in numerous tasks in reinforcement learning. Their theoretical understanding in multiagent settings, however, remains limited, especially beyond two-player competitive and potential Markov games. In this paper, we develop a new framework to characterize optimistic policy gradient methods in multi-player Markov games with a single controller. Specifically, under the further assumption that the game exhibits an equilibrium collapse, in that the marginals of coarse correlated equilibria (CCE) induce Nash equilibria (NE), we show convergence to stationary $\epsilon$-NE in $O(1/\epsilon^2)$ iterations, where $O(\cdot)$ suppresses polynomial factors in the natural parameters of the game. Such an equilibrium collapse is well-known to manifest itself in two-player zero-sum Markov games, but also occurs even in a class of multi-player Markov games with separable interactions, as established by recent work. As a result, we bypass known complexity barriers for computing stationary NE when either of our assumptions fails. Our approach relies on a natural generalization of the classical Minty property that we introduce, which we anticipate to have further applications beyond Markov games.