Efficiently Computing Nash Equilibria in Adversarial Team Markov Games

Computing Nash equilibrium policies is a central problem in multi-agent reinforcement learning that has received extensive attention both in theory and in practice. However, provable guarantees have been thus far either limited to fully competitive or cooperative scenarios or impose strong assumptions that are difficult to meet in most practical applications. In this work, we depart from those prior results by investigating infinite-horizon \emph{adversarial team Markov games}, a natural and well-motivated class of games in which a team of identically-interested players -- in the absence of any explicit coordination or communication -- is competing against an adversarial player. This setting allows for a unifying treatment of zero-sum Markov games and Markov potential games, and serves as a step to model more realistic strategic interactions that feature both competing and cooperative interests. Our main contribution is the first algorithm for computing stationary $\epsilon$-approximate Nash equilibria in adversarial team Markov games with computational complexity that is polynomial in all the natural parameters of the game, as well as $1/\epsilon$. The proposed algorithm is particularly natural and practical, and it is based on performing independent policy gradient steps for each player in the team, in tandem with best responses from the side of the adversary; in turn, the policy for the adversary is then obtained by solving a carefully constructed linear program. Our analysis leverages non-standard techniques to establish the KKT optimality conditions for a nonlinear program with nonconvex constraints, thereby leading to a natural interpretation of the induced Lagrange multipliers. Along the way, we significantly extend an important characterization of optimal policies in adversarial (normal-form) team games due to Von Stengel and Koller (GEB `97).

Teamwork makes von Neumann work: Min-Max Optimization in Two-Team Zero-Sum Games

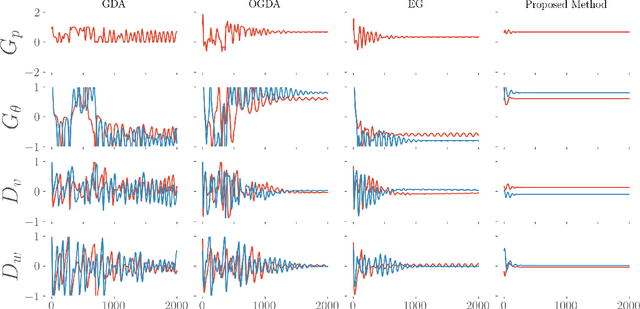
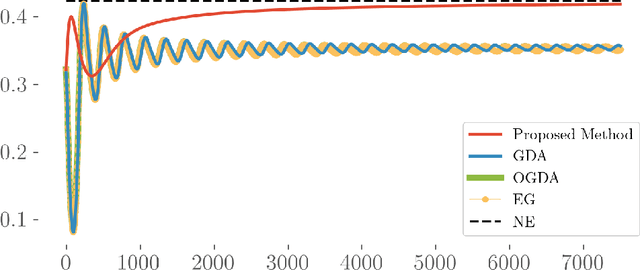
Motivated by recent advances in both theoretical and applied aspects of multiplayer games, spanning from e-sports to multi-agent generative adversarial networks, we focus on min-max optimization in team zero-sum games. In this class of games, players are split into two teams with payoffs equal within the same team and of opposite sign across the opponent team. Unlike the textbook two-player zero-sum games, finding a Nash equilibrium in our class can be shown to be CLS-hard, i.e., it is unlikely to have a polynomial-time algorithm for computing Nash equilibria. Moreover, in this generalized framework, we establish that even asymptotic last iterate or time average convergence to a Nash Equilibrium is not possible using Gradient Descent Ascent (GDA), its optimistic variant, and extra gradient. Specifically, we present a family of team games whose induced utility is \emph{non} multi-linear with \emph{non} attractive \emph{per-se} mixed Nash Equilibria, as strict saddle points of the underlying optimization landscape. Leveraging techniques from control theory, we complement these negative results by designing a modified GDA that converges locally to Nash equilibria. Finally, we discuss connections of our framework with AI architectures with team competition structures like multi-agent generative adversarial networks.