Efficiently Computing Nash Equilibria in Adversarial Team Markov Games

Computing Nash equilibrium policies is a central problem in multi-agent reinforcement learning that has received extensive attention both in theory and in practice. However, provable guarantees have been thus far either limited to fully competitive or cooperative scenarios or impose strong assumptions that are difficult to meet in most practical applications. In this work, we depart from those prior results by investigating infinite-horizon \emph{adversarial team Markov games}, a natural and well-motivated class of games in which a team of identically-interested players -- in the absence of any explicit coordination or communication -- is competing against an adversarial player. This setting allows for a unifying treatment of zero-sum Markov games and Markov potential games, and serves as a step to model more realistic strategic interactions that feature both competing and cooperative interests. Our main contribution is the first algorithm for computing stationary $\epsilon$-approximate Nash equilibria in adversarial team Markov games with computational complexity that is polynomial in all the natural parameters of the game, as well as $1/\epsilon$. The proposed algorithm is particularly natural and practical, and it is based on performing independent policy gradient steps for each player in the team, in tandem with best responses from the side of the adversary; in turn, the policy for the adversary is then obtained by solving a carefully constructed linear program. Our analysis leverages non-standard techniques to establish the KKT optimality conditions for a nonlinear program with nonconvex constraints, thereby leading to a natural interpretation of the induced Lagrange multipliers. Along the way, we significantly extend an important characterization of optimal policies in adversarial (normal-form) team games due to Von Stengel and Koller (GEB `97).

Reinforcement Learning for Location-Aware Scheduling

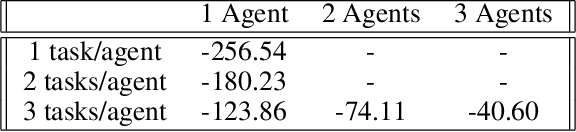
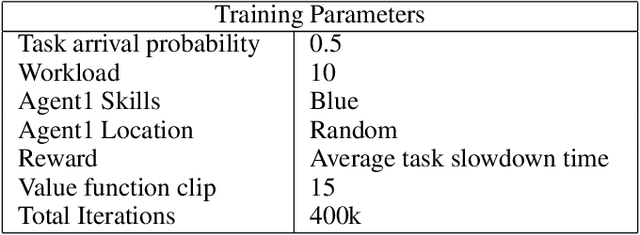
Recent techniques in dynamical scheduling and resource management have found applications in warehouse environments due to their ability to organize and prioritize tasks in a higher temporal resolution. The rise of deep reinforcement learning, as a learning paradigm, has enabled decentralized agent populations to discover complex coordination strategies. However, training multiple agents simultaneously introduce many obstacles in training as observation and action spaces become exponentially large. In our work, we experimentally quantify how various aspects of the warehouse environment (e.g., floor plan complexity, information about agents' live location, level of task parallelizability) affect performance and execution priority. To achieve efficiency, we propose a compact representation of the state and action space for location-aware multi-agent systems, wherein each agent has knowledge of only self and task coordinates, hence only partial observability of the underlying Markov Decision Process. Finally, we show how agents trained in certain environments maintain performance in completely unseen settings and also correlate performance degradation with floor plan geometry.