Filtering through a topological lens: homology for point processes on the time-frequency plane

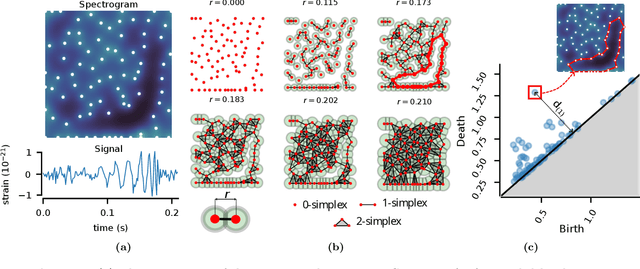
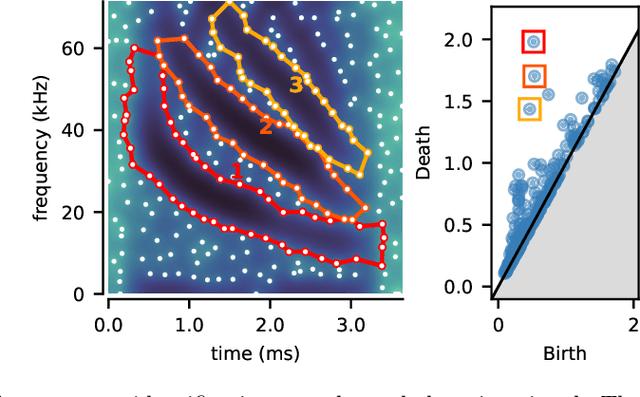
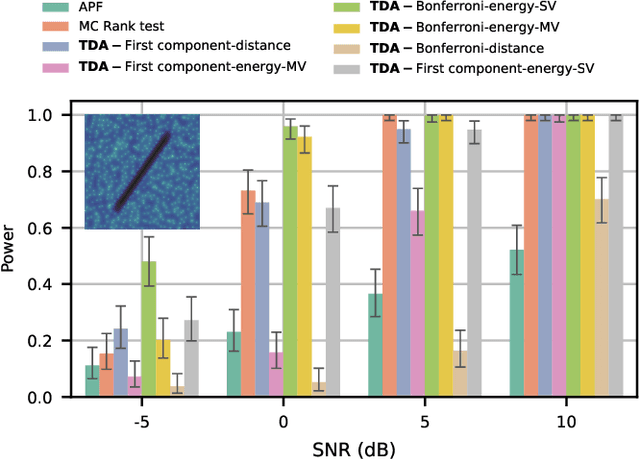
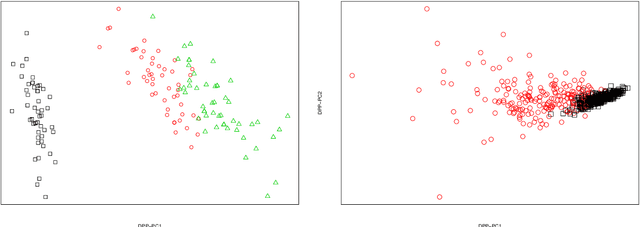
We introduce a very general approach to the analysis of signals from their noisy measurements from the perspective of Topological Data Analysis (TDA). While TDA has emerged as a powerful analytical tool for data with pronounced topological structures, here we demonstrate its applicability for general problems of signal processing, without any a-priori geometric feature. Our methods are well-suited to a wide array of time-dependent signals in different scientific domains, with acoustic signals being a particularly important application. We invoke time-frequency representations of such signals, focusing on their zeros which are gaining salience as a signal processing tool in view of their stability properties. Leveraging state-of-the-art topological concepts, such as stable and minimal volumes, we develop a complete suite of TDA-based methods to explore the delicate stochastic geometry of these zeros, capturing signals based on the disruption they cause to this rigid, hyperuniform spatial structure. Unlike classical spatial data tools, TDA is able to capture the full spectrum of the stochastic geometry of the zeros, thereby leading to powerful inferential outcomes that are underpinned by a principled statistical foundation. This is reflected in the power and versatility of our applications, which include competitive performance in processing. a wide variety of audio signals (esp. in low SNR regimes), effective detection and reconstruction of gravitational wave signals (a reputed signal processing challenge with non-Gaussian noise), and medical time series data from EEGs, indicating a wide horizon for the approach and methods introduced in this paper.

Negative Dependence as a toolbox for machine learning : review and new developments

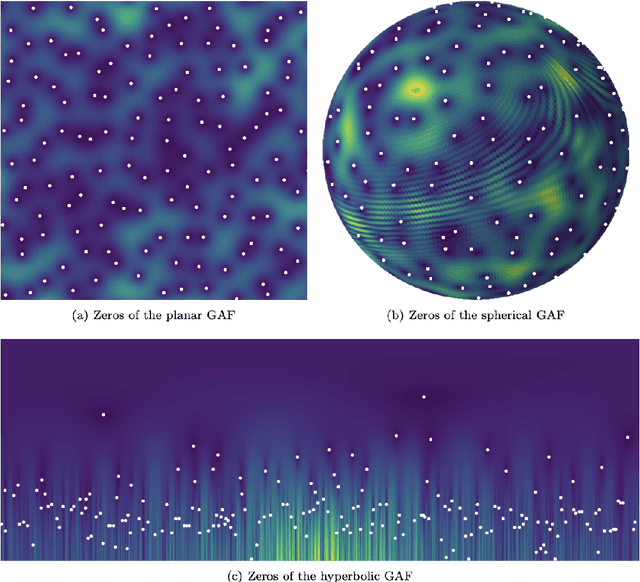
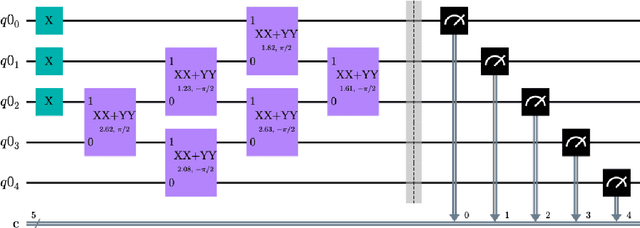
Negative dependence is becoming a key driver in advancing learning capabilities beyond the limits of traditional independence. Recent developments have evidenced support towards negatively dependent systems as a learning paradigm in a broad range of fundamental machine learning challenges including optimization, sampling, dimensionality reduction and sparse signal recovery, often surpassing the performance of current methods based on statistical independence. The most popular negatively dependent model has been that of determinantal point processes (DPPs), which have their origins in quantum theory. However, other models, such as perturbed lattice models, strongly Rayleigh measures, zeros of random functions have gained salience in various learning applications. In this article, we review this burgeoning field of research, as it has developed over the past two decades or so. We also present new results on applications of DPPs to the parsimonious representation of neural networks. In the limited scope of the article, we mostly focus on aspects of this area to which the authors contributed over the recent years, including applications to Monte Carlo methods, coresets and stochastic gradient descent, stochastic networks, signal processing and connections to quantum computation. However, starting from basics of negative dependence for the uninitiated reader, extensive references are provided to a broad swath of related developments which could not be covered within our limited scope. While existing works and reviews generally focus on specific negatively dependent models (e.g. DPPs), a notable feature of this article is that it addresses negative dependence as a machine learning methodology as a whole. In this vein, it covers within its span an array of negatively dependent models and their applications well beyond DPPs, thereby putting forward a very general and rather unique perspective.

Small coresets via negative dependence: DPPs, linear statistics, and concentration

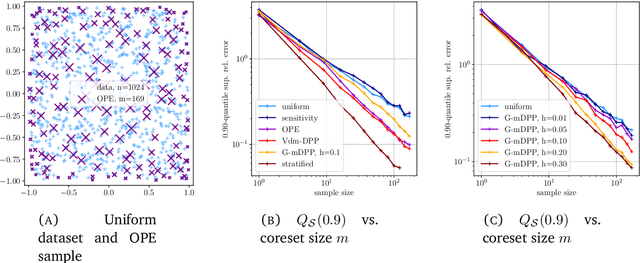
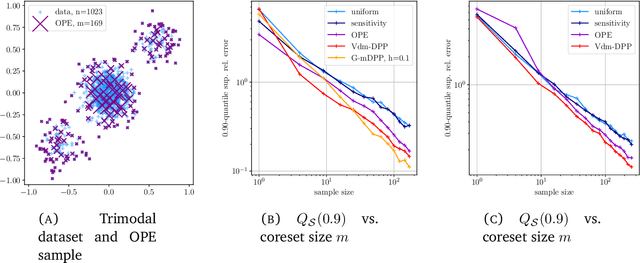
Determinantal point processes (DPPs) are random configurations of points with tunable negative dependence. Because sampling is tractable, DPPs are natural candidates for subsampling tasks, such as minibatch selection or coreset construction. A \emph{coreset} is a subset of a (large) training set, such that minimizing an empirical loss averaged over the coreset is a controlled replacement for the intractable minimization of the original empirical loss. Typically, the control takes the form of a guarantee that the average loss over the coreset approximates the total loss uniformly across the parameter space. Recent work has provided significant empirical support in favor of using DPPs to build randomized coresets, coupled with interesting theoretical results that are suggestive but leave some key questions unanswered. In particular, the central question of whether the cardinality of a DPP-based coreset is fundamentally smaller than one based on independent sampling remained open. In this paper, we answer this question in the affirmative, demonstrating that \emph{DPPs can provably outperform independently drawn coresets}. In this vein, we contribute a conceptual understanding of coreset loss as a \emph{linear statistic} of the (random) coreset. We leverage this structural observation to connect the coresets problem to a more general problem of concentration phenomena for linear statistics of DPPs, wherein we obtain \emph{effective concentration inequalities that extend well-beyond the state-of-the-art}, encompassing general non-projection, even non-symmetric kernels. The latter have been recently shown to be of interest in machine learning beyond coresets, but come with a limited theoretical toolbox, to the extension of which our result contributes. Finally, we are also able to address the coresets problem for vector-valued objective functions, a novelty in the coresets literature.

Dictionary Learning under Symmetries via Group Representations

The dictionary learning problem can be viewed as a data-driven process to learn a suitable transformation so that data is sparsely represented directly from example data. In this paper, we examine the problem of learning a dictionary that is invariant under a pre-specified group of transformations. Natural settings include Cryo-EM, multi-object tracking, synchronization, pose estimation, etc. We specifically study this problem under the lens of mathematical representation theory. Leveraging the power of non-abelian Fourier analysis for functions over compact groups, we prescribe an algorithmic recipe for learning dictionaries that obey such invariances. We relate the dictionary learning problem in the physical domain, which is naturally modelled as being infinite dimensional, with the associated computational problem, which is necessarily finite dimensional. We establish that the dictionary learning problem can be effectively understood as an optimization instance over certain matrix orbitopes having a particular block-diagonal structure governed by the irreducible representations of the group of symmetries. This perspective enables us to introduce a band-limiting procedure which obtains dimensionality reduction in applications. We provide guarantees for our computational ansatz to provide a desirable dictionary learning outcome. We apply our paradigm to investigate the dictionary learning problem for the groups SO(2) and SO(3). While the SO(2) orbitope admits an exact spectrahedral description, substantially less is understood about the SO(3) orbitope. We describe a tractable spectrahedral outer approximation of the SO(3) orbitope, and contribute an alternating minimization paradigm to perform optimization in this setting. We provide numerical experiments to highlight the efficacy of our approach in learning SO(3) invariant dictionaries, both on synthetic and on real world data.

Generative Principal Component Analysis

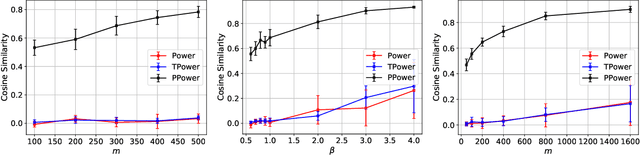
In this paper, we study the problem of principal component analysis with generative modeling assumptions, adopting a general model for the observed matrix that encompasses notable special cases, including spiked matrix recovery and phase retrieval. The key assumption is that the underlying signal lies near the range of an $L$-Lipschitz continuous generative model with bounded $k$-dimensional inputs. We propose a quadratic estimator, and show that it enjoys a statistical rate of order $\sqrt{\frac{k\log L}{m}}$, where $m$ is the number of samples. We also provide a near-matching algorithm-independent lower bound. Moreover, we provide a variant of the classic power method, which projects the calculated data onto the range of the generative model during each iteration. We show that under suitable conditions, this method converges exponentially fast to a point achieving the above-mentioned statistical rate. We perform experiments on various image datasets for spiked matrix and phase retrieval models, and illustrate performance gains of our method to the classic power method and the truncated power method devised for sparse principal component analysis.

Learning with latent group sparsity via heat flow dynamics on networks

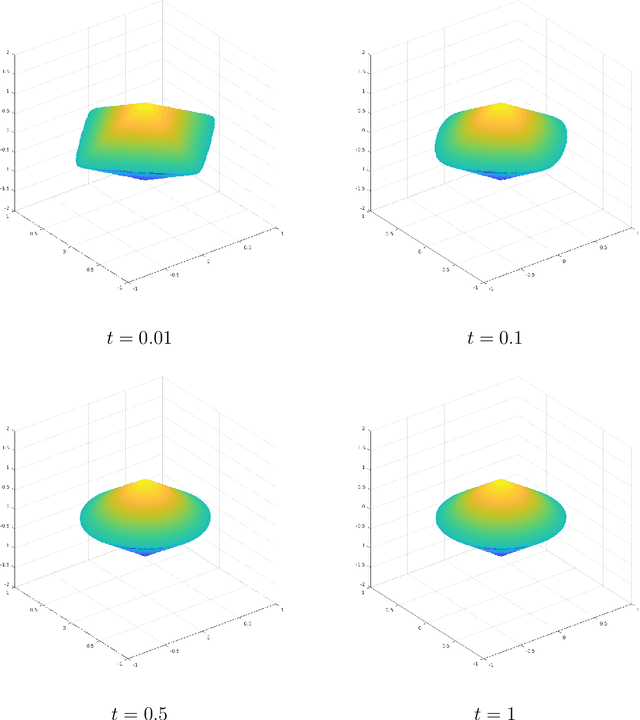
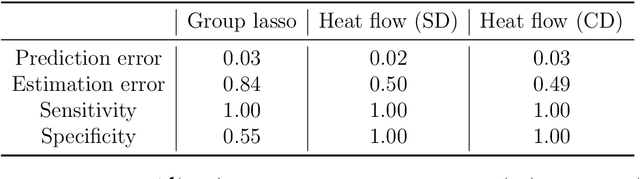
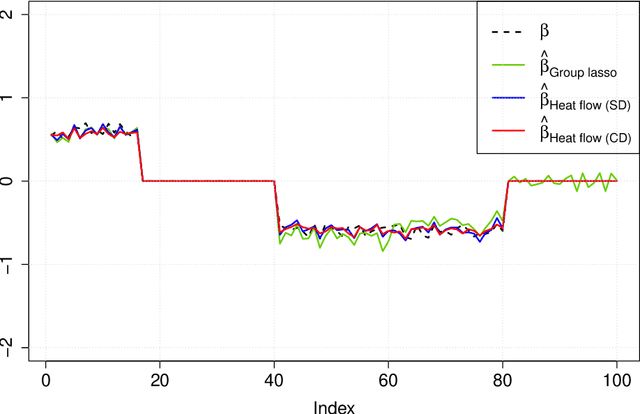
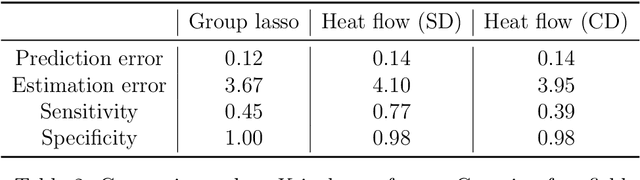
Group or cluster structure on explanatory variables in machine learning problems is a very general phenomenon, which has attracted broad interest from practitioners and theoreticians alike. In this work we contribute an approach to learning under such group structure, that does not require prior information on the group identities. Our paradigm is motivated by the Laplacian geometry of an underlying network with a related community structure, and proceeds by directly incorporating this into a penalty that is effectively computed via a heat flow-based local network dynamics. In fact, we demonstrate a procedure to construct such a network based on the available data. Notably, we dispense with computationally intensive pre-processing involving clustering of variables, spectral or otherwise. Our technique is underpinned by rigorous theorems that guarantee its effective performance and provide bounds on its sample complexity. In particular, in a wide range of settings, it provably suffices to run the heat flow dynamics for time that is only logarithmic in the problem dimensions. We explore in detail the interfaces of our approach with key statistical physics models in network science, such as the Gaussian Free Field and the Stochastic Block Model. We validate our approach by successful applications to real-world data from a wide array of application domains, including computer science, genetics, climatology and economics. Our work raises the possibility of applying similar diffusion-based techniques to classical learning tasks, exploiting the interplay between geometric, dynamical and stochastic structures underlying the data.

Robust 1-bit Compressive Sensing with Partial Gaussian Circulant Matrices and Generative Priors

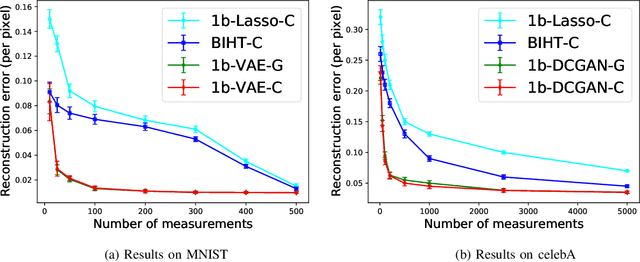
In 1-bit compressive sensing, each measurement is quantized to a single bit, namely the sign of a linear function of an unknown vector, and the goal is to accurately recover the vector. While it is most popular to assume a standard Gaussian sensing matrix for 1-bit compressive sensing, using structured sensing matrices such as partial Gaussian circulant matrices is of significant practical importance due to their faster matrix operations. In this paper, we provide recovery guarantees for a correlation-based optimization algorithm for robust 1-bit compressive sensing with randomly signed partial Gaussian circulant matrices and generative models. Under suitable assumptions, we match guarantees that were previously only known to hold for i.i.d.~Gaussian matrices that require significantly more computation. We make use of a practical iterative algorithm, and perform numerical experiments on image datasets to corroborate our theoretical results.

Towards Sample-Optimal Compressive Phase Retrieval with Sparse and Generative Priors

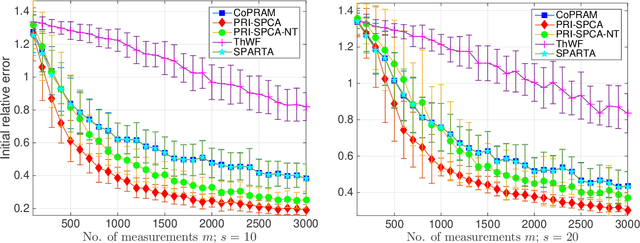
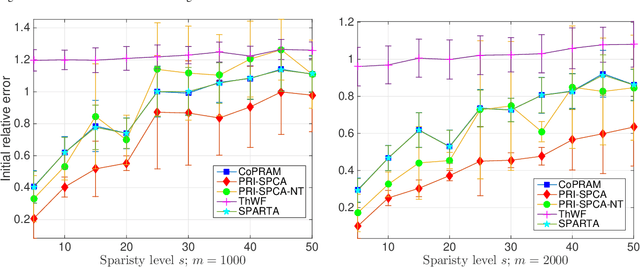
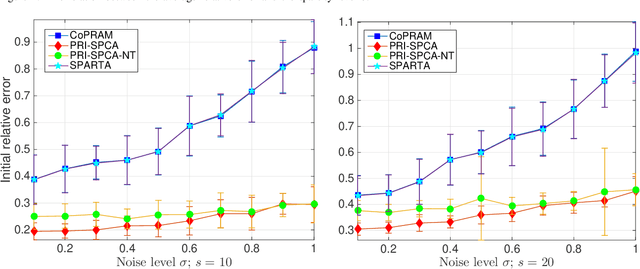
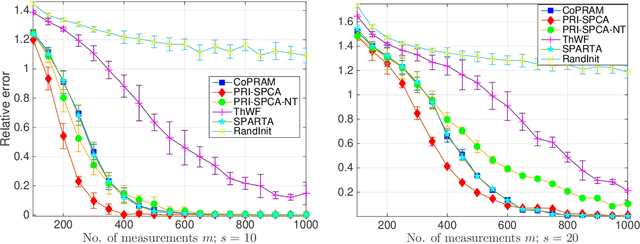
Compressive phase retrieval is a popular variant of the standard compressive sensing problem, in which the measurements only contain magnitude information. In this paper, motivated by recent advances in deep generative models, we provide recovery guarantees with order-optimal sample complexity bounds for phase retrieval with generative priors. We first show that when using i.i.d. Gaussian measurements and an $L$-Lipschitz continuous generative model with bounded $k$-dimensional inputs, roughly $O(k \log L)$ samples suffice to guarantee that the signal is close to any vector that minimizes an amplitude-based empirical loss function. Attaining this sample complexity with a practical algorithm remains a difficult challenge, and a popular spectral initialization method has been observed to pose a major bottleneck. To partially address this, we further show that roughly $O(k \log L)$ samples ensure sufficient closeness between the signal and any {\em globally optimal} solution to an optimization problem designed for spectral initialization (though finding such a solution may still be challenging). We adapt this result to sparse phase retrieval, and show that $O(s \log n)$ samples are sufficient for a similar guarantee when the underlying signal is $s$-sparse and $n$-dimensional, matching an information-theoretic lower bound. While our guarantees do not directly correspond to a practical algorithm, we propose a practical spectral initialization method motivated by our findings, and experimentally observe significant performance gains over various existing spectral initialization methods of sparse phase retrieval.

Estimation and inference of signals via the stochastic geometry of spectrogram level sets

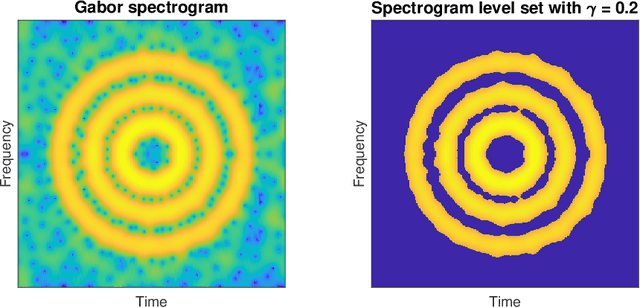
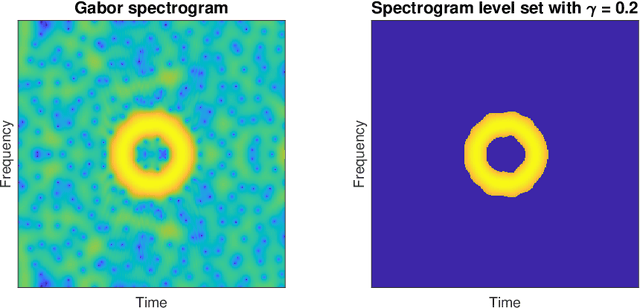
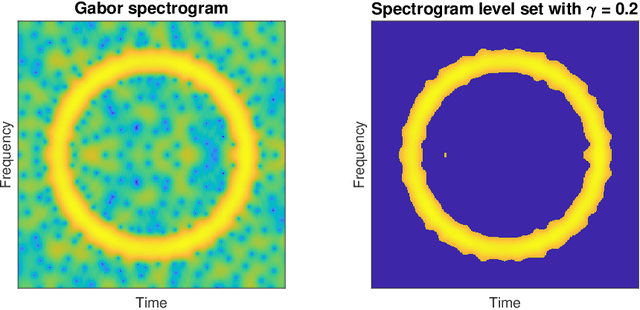
Spectrograms are fundamental tools in the detection, estimation and analysis of signals in the time-frequency analysis paradigm. Signal analysis via spectrograms have traditionally explored their peaks, i.e. their maxima, complemented by a recent interest in their zeros or minima. In particular, recent investigations have demonstrated connections between Gabor spectrograms of Gaussian white noise and Gaussian analytic functions (abbrv. GAFs) in different geometries. However, the zero sets (or the maxima or minima) of GAFs have a complicated stochastic structure, which makes a direct theoretical analysis of usual spectrogram based techniques via GAFs a difficult proposition. These techniques, in turn, largely rely on statistical observables from the analysis of spatial data, whose distributional properties for spectrogram extrema are mostly understood empirically. In this work, we investigate spectrogram analysis via an examination of the stochastic, geometric and analytical properties of their level sets. This includes a comparative analysis of relevant spectrogram structures, with vs without the presence of signals coupled with Gaussian white noise. We obtain theorems demonstrating the efficacy of a spectrogram level sets based approach to the detection and estimation of signals, framed in a concrete inferential set-up. Exploiting these ideas as theoretical underpinnings, we propose a level sets based algorithm for signal analysis that is intrinsic to given spectrogram data. We substantiate the effectiveness of the algorithm by extensive empirical studies, and provide additional theoretical analysis to elucidate some of its key features. Our results also have theoretical implications for spectrogram zero based approaches to signal analysis.

On a Variational Approximation based Empirical Likelihood ABC Method

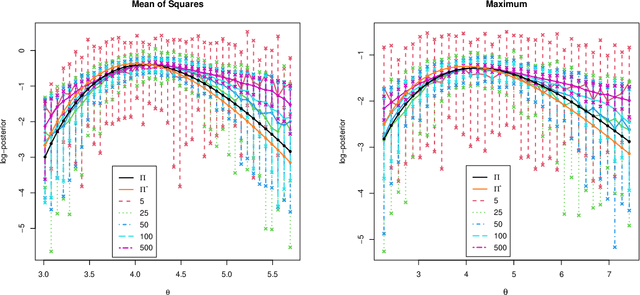
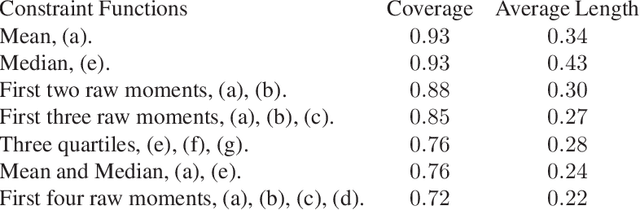
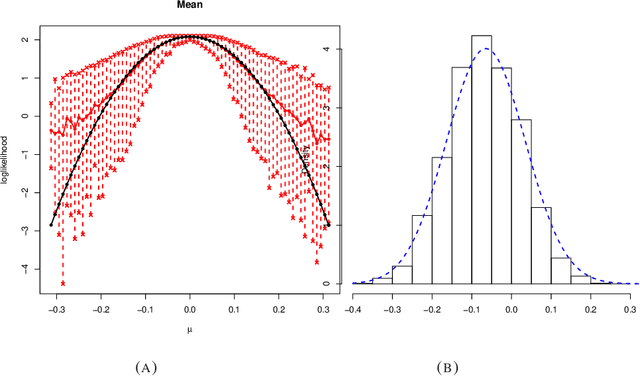
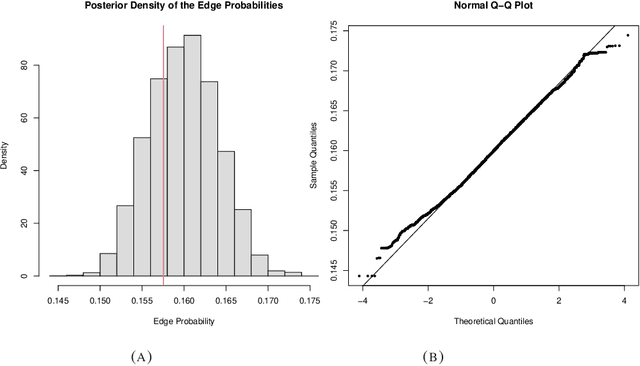
Many scientifically well-motivated statistical models in natural, engineering, and environmental sciences are specified through a generative process. However, in some cases, it may not be possible to write down the likelihood for these models analytically. Approximate Bayesian computation (ABC) methods allow Bayesian inference in such situations. The procedures are nonetheless typically computationally intensive. Recently, computationally attractive empirical likelihood-based ABC methods have been suggested in the literature. All of these methods rely on the availability of several suitable analytically tractable estimating equations, and this is sometimes problematic. We propose an easy-to-use empirical likelihood ABC method in this article. First, by using a variational approximation argument as a motivation, we show that the target log-posterior can be approximated as a sum of an expected joint log-likelihood and the differential entropy of the data generating density. The expected log-likelihood is then estimated by an empirical likelihood where the only inputs required are a choice of summary statistic, it's observed value, and the ability to simulate the chosen summary statistics for any parameter value under the model. The differential entropy is estimated from the simulated summaries using traditional methods. Posterior consistency is established for the method, and we discuss the bounds for the required number of simulated summaries in detail. The performance of the proposed method is explored in various examples.