Kin Aun Tan
Filtering through a topological lens: homology for point processes on the time-frequency plane
Apr 10, 2025
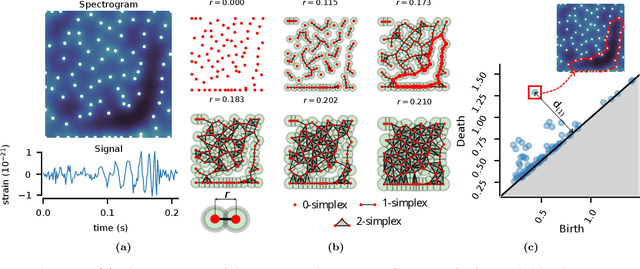
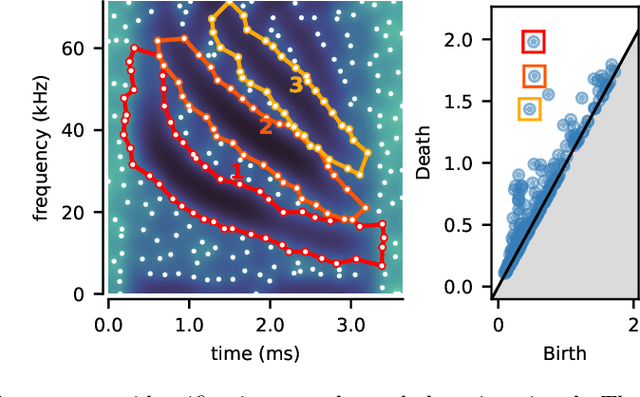
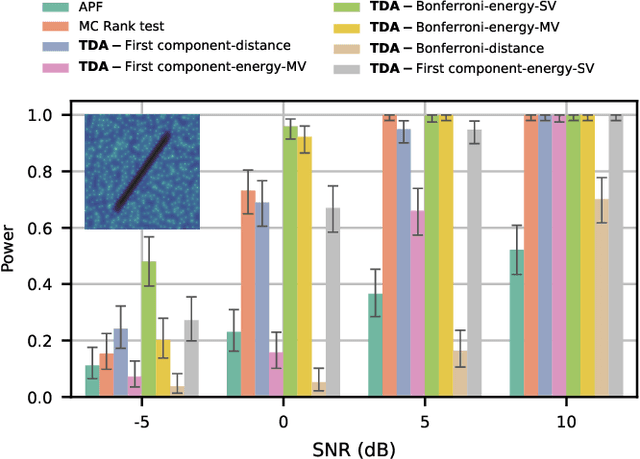
Abstract:We introduce a very general approach to the analysis of signals from their noisy measurements from the perspective of Topological Data Analysis (TDA). While TDA has emerged as a powerful analytical tool for data with pronounced topological structures, here we demonstrate its applicability for general problems of signal processing, without any a-priori geometric feature. Our methods are well-suited to a wide array of time-dependent signals in different scientific domains, with acoustic signals being a particularly important application. We invoke time-frequency representations of such signals, focusing on their zeros which are gaining salience as a signal processing tool in view of their stability properties. Leveraging state-of-the-art topological concepts, such as stable and minimal volumes, we develop a complete suite of TDA-based methods to explore the delicate stochastic geometry of these zeros, capturing signals based on the disruption they cause to this rigid, hyperuniform spatial structure. Unlike classical spatial data tools, TDA is able to capture the full spectrum of the stochastic geometry of the zeros, thereby leading to powerful inferential outcomes that are underpinned by a principled statistical foundation. This is reflected in the power and versatility of our applications, which include competitive performance in processing. a wide variety of audio signals (esp. in low SNR regimes), effective detection and reconstruction of gravitational wave signals (a reputed signal processing challenge with non-Gaussian noise), and medical time series data from EEGs, indicating a wide horizon for the approach and methods introduced in this paper.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge