Filtering through a topological lens: homology for point processes on the time-frequency plane

We introduce a very general approach to the analysis of signals from their noisy measurements from the perspective of Topological Data Analysis (TDA). While TDA has emerged as a powerful analytical tool for data with pronounced topological structures, here we demonstrate its applicability for general problems of signal processing, without any a-priori geometric feature. Our methods are well-suited to a wide array of time-dependent signals in different scientific domains, with acoustic signals being a particularly important application. We invoke time-frequency representations of such signals, focusing on their zeros which are gaining salience as a signal processing tool in view of their stability properties. Leveraging state-of-the-art topological concepts, such as stable and minimal volumes, we develop a complete suite of TDA-based methods to explore the delicate stochastic geometry of these zeros, capturing signals based on the disruption they cause to this rigid, hyperuniform spatial structure. Unlike classical spatial data tools, TDA is able to capture the full spectrum of the stochastic geometry of the zeros, thereby leading to powerful inferential outcomes that are underpinned by a principled statistical foundation. This is reflected in the power and versatility of our applications, which include competitive performance in processing. a wide variety of audio signals (esp. in low SNR regimes), effective detection and reconstruction of gravitational wave signals (a reputed signal processing challenge with non-Gaussian noise), and medical time series data from EEGs, indicating a wide horizon for the approach and methods introduced in this paper.

LASER: A new method for locally adaptive nonparametric regression

In this article, we introduce \textsf{LASER} (Locally Adaptive Smoothing Estimator for Regression), a computationally efficient locally adaptive nonparametric regression method that performs variable bandwidth local polynomial regression. We prove that it adapts (near-)optimally to the local H\"{o}lder exponent of the underlying regression function \texttt{simultaneously} at all points in its domain. Furthermore, we show that there is a single ideal choice of a global tuning parameter under which the above mentioned local adaptivity holds. Despite the vast literature on nonparametric regression, instances of practicable methods with provable guarantees of such a strong notion of local adaptivity are rare. The proposed method achieves excellent performance across a broad range of numerical experiments in comparison to popular alternative locally adaptive methods.

Transfer Learning for Latent Variable Network Models

We study transfer learning for estimation in latent variable network models. In our setting, the conditional edge probability matrices given the latent variables are represented by $P$ for the source and $Q$ for the target. We wish to estimate $Q$ given two kinds of data: (1) edge data from a subgraph induced by an $o(1)$ fraction of the nodes of $Q$, and (2) edge data from all of $P$. If the source $P$ has no relation to the target $Q$, the estimation error must be $\Omega(1)$. However, we show that if the latent variables are shared, then vanishing error is possible. We give an efficient algorithm that utilizes the ordering of a suitably defined graph distance. Our algorithm achieves $o(1)$ error and does not assume a parametric form on the source or target networks. Next, for the specific case of Stochastic Block Models we prove a minimax lower bound and show that a simple algorithm achieves this rate. Finally, we empirically demonstrate our algorithm's use on real-world and simulated graph transfer problems.

Implicit Regularization via Spectral Neural Networks and Non-linear Matrix Sensing

The phenomenon of implicit regularization has attracted interest in recent years as a fundamental aspect of the remarkable generalizing ability of neural networks. In a nutshell, it entails that gradient descent dynamics in many neural nets, even without any explicit regularizer in the loss function, converges to the solution of a regularized learning problem. However, known results attempting to theoretically explain this phenomenon focus overwhelmingly on the setting of linear neural nets, and the simplicity of the linear structure is particularly crucial to existing arguments. In this paper, we explore this problem in the context of more realistic neural networks with a general class of non-linear activation functions, and rigorously demonstrate the implicit regularization phenomenon for such networks in the setting of matrix sensing problems, together with rigorous rate guarantees that ensure exponentially fast convergence of gradient descent.In this vein, we contribute a network architecture called Spectral Neural Networks (abbrv. SNN) that is particularly suitable for matrix learning problems. Conceptually, this entails coordinatizing the space of matrices by their singular values and singular vectors, as opposed to by their entries, a potentially fruitful perspective for matrix learning. We demonstrate that the SNN architecture is inherently much more amenable to theoretical analysis than vanilla neural nets and confirm its effectiveness in the context of matrix sensing, via both mathematical guarantees and empirical investigations. We believe that the SNN architecture has the potential to be of wide applicability in a broad class of matrix learning scenarios.

Minimax-optimal estimation for sparse multi-reference alignment with collision-free signals

The Multi-Reference Alignment (MRA) problem aims at the recovery of an unknown signal from repeated observations under the latent action of a group of cyclic isometries, in the presence of additive noise of high intensity $\sigma$. It is a more tractable version of the celebrated cryo EM model. In the crucial high noise regime, it is known that its sample complexity scales as $\sigma^6$. Recent investigations have shown that for the practically significant setting of sparse signals, the sample complexity of the maximum likelihood estimator asymptotically scales with the noise level as $\sigma^4$. In this work, we investigate minimax optimality for signal estimation under the MRA model for so-called collision-free signals. In particular, this signal class covers the setting of generic signals of dilute sparsity (wherein the support size $s=O(L^{1/3})$, where $L$ is the ambient dimension. We demonstrate that the minimax optimal rate of estimation in for the sparse MRA problem in this setting is $\sigma^2/\sqrt{n}$, where $n$ is the sample size. In particular, this widely generalizes the sample complexity asymptotics for the restricted MLE in this setting, establishing it as the statistically optimal estimator. Finally, we demonstrate a concentration inequality for the restricted MLE on its deviations from the ground truth.

Learning Networks from Gaussian Graphical Models and Gaussian Free Fields

We investigate the problem of estimating the structure of a weighted network from repeated measurements of a Gaussian Graphical Model (GGM) on the network. In this vein, we consider GGMs whose covariance structures align with the geometry of the weighted network on which they are based. Such GGMs have been of longstanding interest in statistical physics, and are referred to as the Gaussian Free Field (GFF). In recent years, they have attracted considerable interest in the machine learning and theoretical computer science. In this work, we propose a novel estimator for the weighted network (equivalently, its Laplacian) from repeated measurements of a GFF on the network, based on the Fourier analytic properties of the Gaussian distribution. In this pursuit, our approach exploits complex-valued statistics constructed from observed data, that are of interest on their own right. We demonstrate the effectiveness of our estimator with concrete recovery guarantees and bounds on the required sample complexity. In particular, we show that the proposed statistic achieves the parametric rate of estimation for fixed network size. In the setting of networks growing with sample size, our results show that for Erdos-Renyi random graphs $G(d,p)$ above the connectivity threshold, we demonstrate that network recovery takes place with high probability as soon as the sample size $n$ satisfies $n \gg d^4 \log d \cdot p^{-2}$.

Consistent model selection in the spiked Wigner model via AIC-type criteria

Consider the spiked Wigner model \[ X = \sum_{i = 1}^k \lambda_i u_i u_i^\top + \sigma G, \] where $G$ is an $N \times N$ GOE random matrix, and the eigenvalues $\lambda_i$ are all spiked, i.e. above the Baik-Ben Arous-P\'ech\'e (BBP) threshold $\sigma$. We consider AIC-type model selection criteria of the form \[ -2 \, (\text{maximised log-likelihood}) + \gamma \, (\text{number of parameters}) \] for estimating the number $k$ of spikes. For $\gamma > 2$, the above criterion is strongly consistent provided $\lambda_k > \lambda_{\gamma}$, where $\lambda_{\gamma}$ is a threshold strictly above the BBP threshold, whereas for $\gamma < 2$, it almost surely overestimates $k$. Although AIC (which corresponds to $\gamma = 2$) is not strongly consistent, we show that taking $\gamma = 2 + \delta_N$, where $\delta_N \to 0$ and $\delta_N \gg N^{-2/3}$, results in a weakly consistent estimator of $k$. We also show that a certain soft minimiser of AIC is strongly consistent.

Wasserstein Projection Pursuit of Non-Gaussian Signals

We consider the general dimensionality reduction problem of locating in a high-dimensional data cloud, a $k$-dimensional non-Gaussian subspace of interesting features. We use a projection pursuit approach -- we search for mutually orthogonal unit directions which maximise the 2-Wasserstein distance of the empirical distribution of data-projections along these directions from a standard Gaussian. Under a generative model, where there is a underlying (unknown) low-dimensional non-Gaussian subspace, we prove rigorous statistical guarantees on the accuracy of approximating this unknown subspace by the directions found by our projection pursuit approach. Our results operate in the regime where the data dimensionality is comparable to the sample size, and thus supplement the recent literature on the non-feasibility of locating interesting directions via projection pursuit in the complementary regime where the data dimensionality is much larger than the sample size.

Concentration inequalities for correlated network-valued processes with applications to community estimation and changepoint analysis

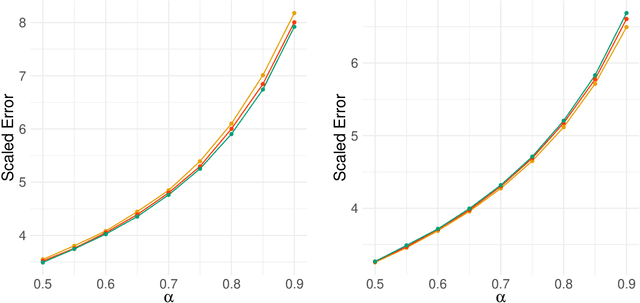
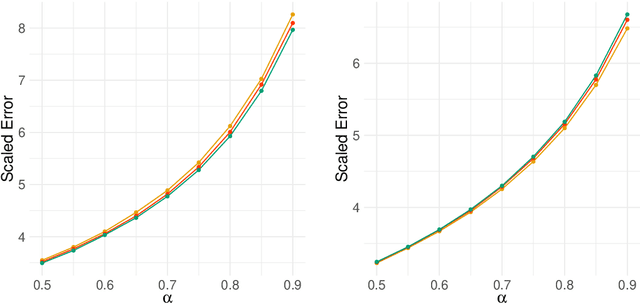
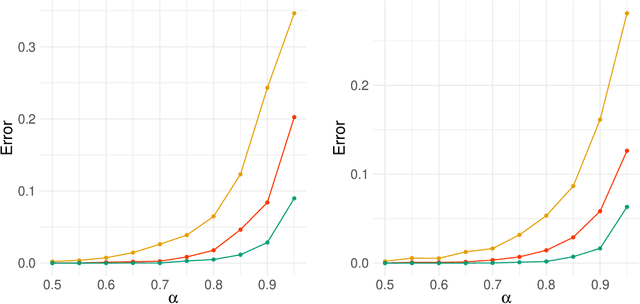
Network-valued time series are currently a common form of network data. However, the study of the aggregate behavior of network sequences generated from network-valued stochastic processes is relatively rare. Most of the existing research focuses on the simple setup where the networks are independent (or conditionally independent) across time, and all edges are updated synchronously at each time step. In this paper, we study the concentration properties of the aggregated adjacency matrix and the corresponding Laplacian matrix associated with network sequences generated from lazy network-valued stochastic processes, where edges update asynchronously, and each edge follows a lazy stochastic process for its updates independent of the other edges. We demonstrate the usefulness of these concentration results in proving consistency of standard estimators in community estimation and changepoint estimation problems. We also conduct a simulation study to demonstrate the effect of the laziness parameter, which controls the extent of temporal correlation, on the accuracy of community and changepoint estimation.

Learning with latent group sparsity via heat flow dynamics on networks

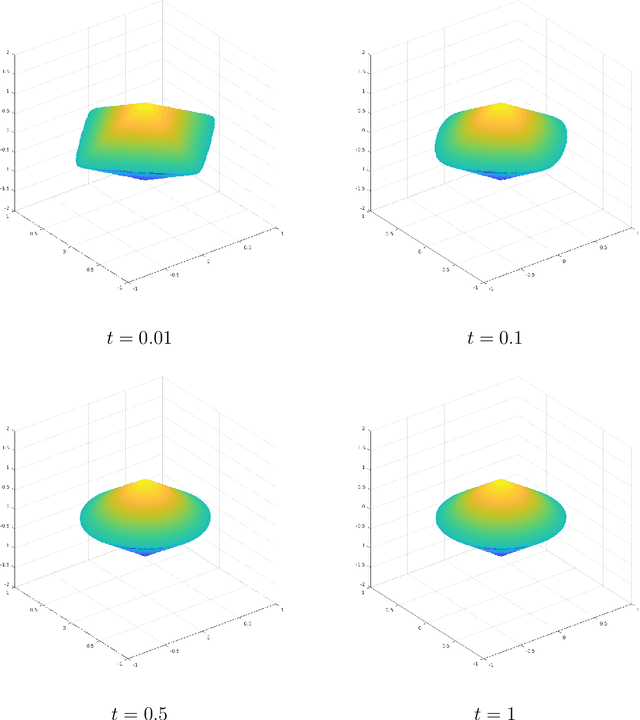
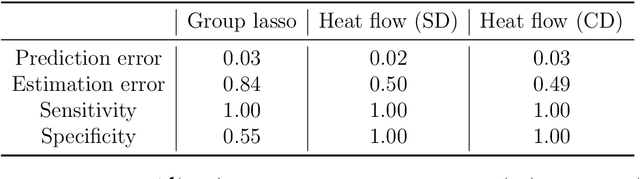
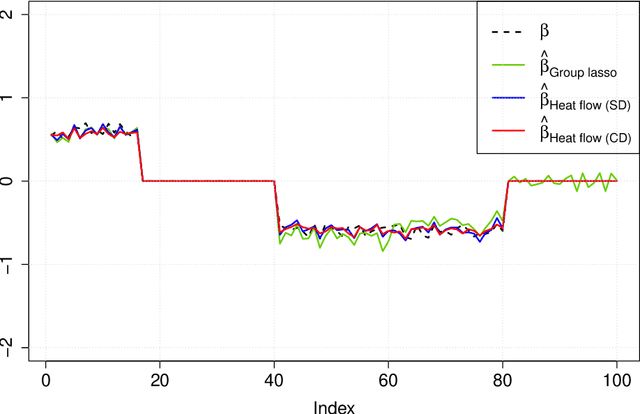
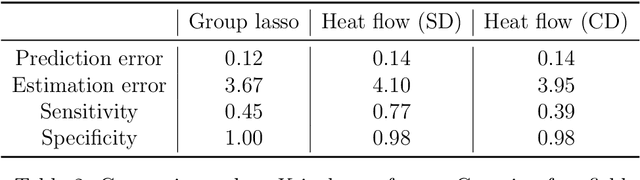
Group or cluster structure on explanatory variables in machine learning problems is a very general phenomenon, which has attracted broad interest from practitioners and theoreticians alike. In this work we contribute an approach to learning under such group structure, that does not require prior information on the group identities. Our paradigm is motivated by the Laplacian geometry of an underlying network with a related community structure, and proceeds by directly incorporating this into a penalty that is effectively computed via a heat flow-based local network dynamics. In fact, we demonstrate a procedure to construct such a network based on the available data. Notably, we dispense with computationally intensive pre-processing involving clustering of variables, spectral or otherwise. Our technique is underpinned by rigorous theorems that guarantee its effective performance and provide bounds on its sample complexity. In particular, in a wide range of settings, it provably suffices to run the heat flow dynamics for time that is only logarithmic in the problem dimensions. We explore in detail the interfaces of our approach with key statistical physics models in network science, such as the Gaussian Free Field and the Stochastic Block Model. We validate our approach by successful applications to real-world data from a wide array of application domains, including computer science, genetics, climatology and economics. Our work raises the possibility of applying similar diffusion-based techniques to classical learning tasks, exploiting the interplay between geometric, dynamical and stochastic structures underlying the data.