Representation Learning Dynamics of Self-Supervised Models

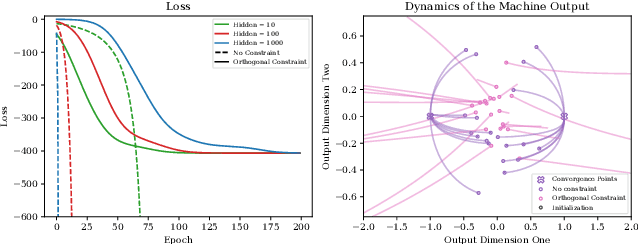
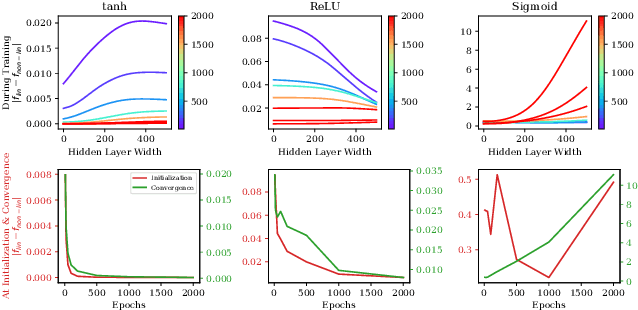
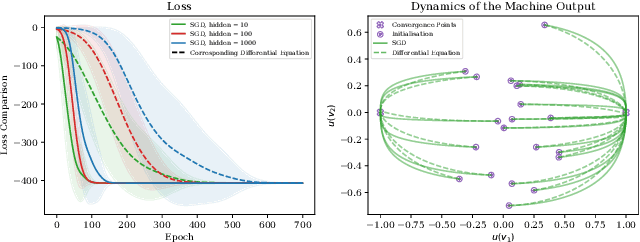
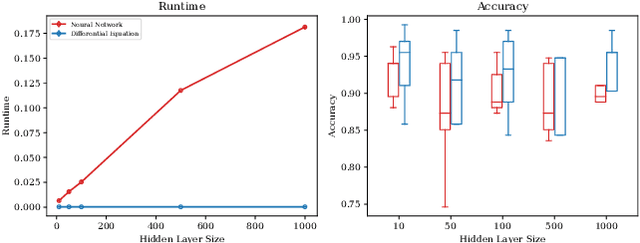
Self-Supervised Learning (SSL) is an important paradigm for learning representations from unlabelled data, and SSL with neural networks has been highly successful in practice. However current theoretical analysis of SSL is mostly restricted to generalisation error bounds. In contrast, learning dynamics often provide a precise characterisation of the behaviour of neural networks based models but, so far, are mainly known in supervised settings. In this paper, we study the learning dynamics of SSL models, specifically representations obtained by minimising contrastive and non-contrastive losses. We show that a naive extension of the dymanics of multivariate regression to SSL leads to learning trivial scalar representations that demonstrates dimension collapse in SSL. Consequently, we formulate SSL objectives with orthogonality constraints on the weights, and derive the exact (network width independent) learning dynamics of the SSL models trained using gradient descent on the Grassmannian manifold. We also argue that the infinite width approximation of SSL models significantly deviate from the neural tangent kernel approximations of supervised models. We numerically illustrate the validity of our theoretical findings, and discuss how the presented results provide a framework for further theoretical analysis of contrastive and non-contrastive SSL.

Wasserstein Projection Pursuit of Non-Gaussian Signals

We consider the general dimensionality reduction problem of locating in a high-dimensional data cloud, a $k$-dimensional non-Gaussian subspace of interesting features. We use a projection pursuit approach -- we search for mutually orthogonal unit directions which maximise the 2-Wasserstein distance of the empirical distribution of data-projections along these directions from a standard Gaussian. Under a generative model, where there is a underlying (unknown) low-dimensional non-Gaussian subspace, we prove rigorous statistical guarantees on the accuracy of approximating this unknown subspace by the directions found by our projection pursuit approach. Our results operate in the regime where the data dimensionality is comparable to the sample size, and thus supplement the recent literature on the non-feasibility of locating interesting directions via projection pursuit in the complementary regime where the data dimensionality is much larger than the sample size.

Improved Representation Learning Through Tensorized Autoencoders

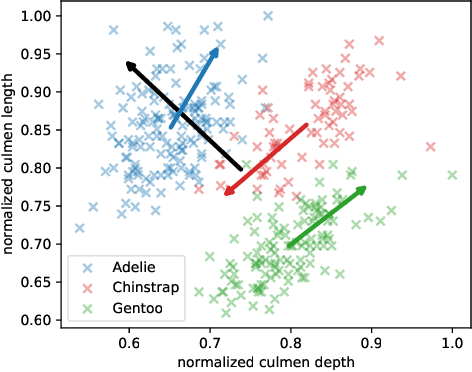
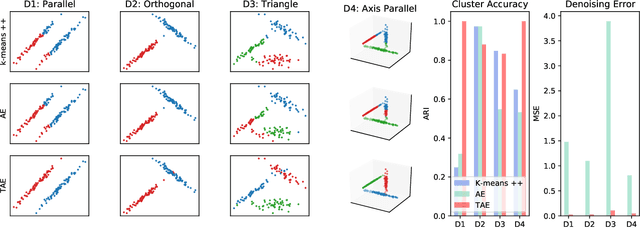
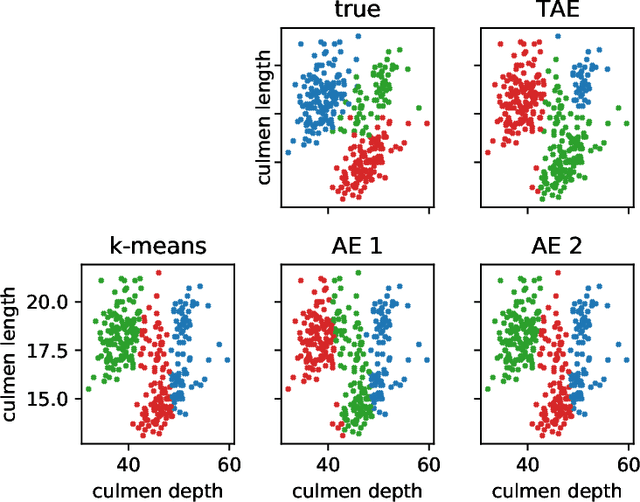
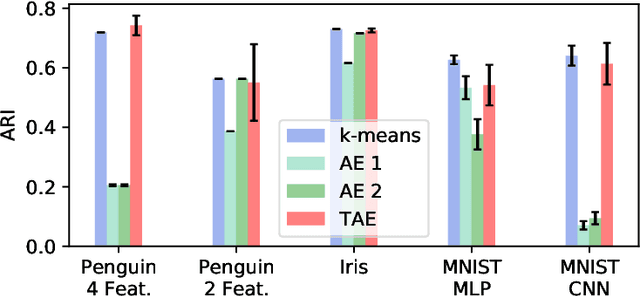
The central question in representation learning is what constitutes a good or meaningful representation. In this work we argue that if we consider data with inherent cluster structures, where clusters can be characterized through different means and covariances, those data structures should be represented in the embedding as well. While Autoencoders (AE) are widely used in practice for unsupervised representation learning, they do not fulfil the above condition on the embedding as they obtain a single representation of the data. To overcome this we propose a meta-algorithm that can be used to extend an arbitrary AE architecture to a tensorized version (TAE) that allows for learning cluster-specific embeddings while simultaneously learning the cluster assignment. For the linear setting we prove that TAE can recover the principle components of the different clusters in contrast to principle component of the entire data recovered by a standard AE. We validated this on planted models and for general, non-linear and convolutional AEs we empirically illustrate that tensorizing the AE is beneficial in clustering and de-noising tasks.