Impact of Bottleneck Layers and Skip Connections on the Generalization of Linear Denoising Autoencoders

Modern deep neural networks exhibit strong generalization even in highly overparameterized regimes. Significant progress has been made to understand this phenomenon in the context of supervised learning, but for unsupervised tasks such as denoising, several open questions remain. While some recent works have successfully characterized the test error of the linear denoising problem, they are limited to linear models (one-layer network). In this work, we focus on two-layer linear denoising autoencoders trained under gradient flow, incorporating two key ingredients of modern deep learning architectures: A low-dimensional bottleneck layer that effectively enforces a rank constraint on the learned solution, as well as the possibility of a skip connection that bypasses the bottleneck. We derive closed-form expressions for all critical points of this model under product regularization, and in particular describe its global minimizer under the minimum-norm principle. From there, we derive the test risk formula in the overparameterized regime, both for models with and without skip connections. Our analysis reveals two interesting phenomena: Firstly, the bottleneck layer introduces an additional complexity measure akin to the classical bias-variance trade-off -- increasing the bottleneck width reduces bias but introduces variance, and vice versa. Secondly, skip connection can mitigate the variance in denoising autoencoders -- especially when the model is mildly overparameterized. We further analyze the impact of skip connections in denoising autoencoder using random matrix theory and support our claims with numerical evidence.

Generalization Certificates for Adversarially Robust Bayesian Linear Regression

Adversarial robustness of machine learning models is critical to ensuring reliable performance under data perturbations. Recent progress has been on point estimators, and this paper considers distributional predictors. First, using the link between exponential families and Bregman divergences, we formulate an adversarial Bregman divergence loss as an adversarial negative log-likelihood. Using the geometric properties of Bregman divergences, we compute the adversarial perturbation for such models in closed-form. Second, under such losses, we introduce \emph{adversarially robust posteriors}, by exploiting the optimization-centric view of generalized Bayesian inference. Third, we derive the \emph{first} rigorous generalization certificates in the context of an adversarial extension of Bayesian linear regression by leveraging the PAC-Bayesian framework. Finally, experiments on real and synthetic datasets demonstrate the superior robustness of the derived adversarially robust posterior over Bayes posterior, and also validate our theoretical guarantees.

Attention Learning is Needed to Efficiently Learn Parity Function

Transformers, with their attention mechanisms, have emerged as the state-of-the-art architectures of sequential modeling and empirically outperform feed-forward neural networks (FFNNs) across many fields, such as natural language processing and computer vision. However, their generalization ability, particularly for low-sensitivity functions, remains less studied. We bridge this gap by analyzing transformers on the $k$-parity problem. Daniely and Malach (NeurIPS 2020) show that FFNNs with one hidden layer and $O(nk^7 \log k)$ parameters can learn $k$-parity, where the input length $n$ is typically much larger than $k$. In this paper, we prove that FFNNs require at least $\Omega(n)$ parameters to learn $k$-parity, while transformers require only $O(k)$ parameters, surpassing the theoretical lower bound needed by FFNNs. We further prove that this parameter efficiency cannot be achieved with fixed attention heads. Our work establishes transformers as theoretically superior to FFNNs in learning parity function, showing how their attention mechanisms enable parameter-efficient generalization in functions with low sensitivity.

Recovering Imbalanced Clusters via Gradient-Based Projection Pursuit

Projection Pursuit is a classic exploratory technique for finding interesting projections of a dataset. We propose a method for recovering projections containing either Imbalanced Clusters or a Bernoulli-Rademacher distribution using a gradient-based technique to optimize the projection index. As sample complexity is a major limiting factor in Projection Pursuit, we analyze our algorithm's sample complexity within a Planted Vector setting where we can observe that Imbalanced Clusters can be recovered more easily than balanced ones. Additionally, we give a generalized result that works for a variety of data distributions and projection indices. We compare these results to computational lower bounds in the Low-Degree-Polynomial Framework. Finally, we experimentally evaluate our method's applicability to real-world data using FashionMNIST and the Human Activity Recognition Dataset, where our algorithm outperforms others when only a few samples are available.

Tight PAC-Bayesian Risk Certificates for Contrastive Learning

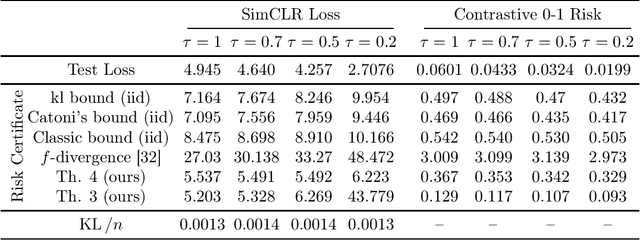
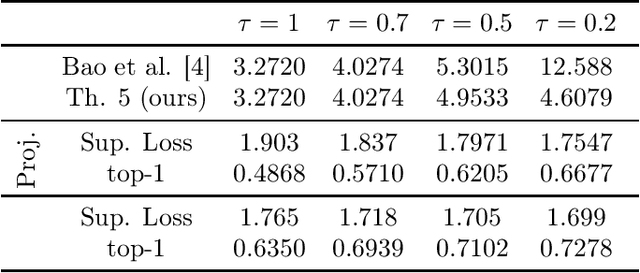
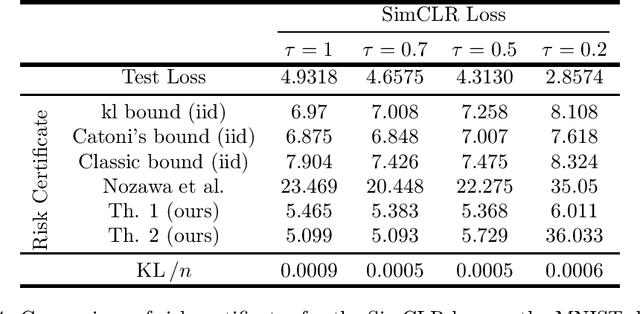
Contrastive representation learning is a modern paradigm for learning representations of unlabeled data via augmentations -- precisely, contrastive models learn to embed semantically similar pairs of samples (positive pairs) closer than independently drawn samples (negative samples). In spite of its empirical success and widespread use in foundation models, statistical theory for contrastive learning remains less explored. Recent works have developed generalization error bounds for contrastive losses, but the resulting risk certificates are either vacuous (certificates based on Rademacher complexity or $f$-divergence) or require strong assumptions about samples that are unreasonable in practice. The present paper develops non-vacuous PAC-Bayesian risk certificates for contrastive representation learning, considering the practical considerations of the popular SimCLR framework. Notably, we take into account that SimCLR reuses positive pairs of augmented data as negative samples for other data, thereby inducing strong dependence and making classical PAC or PAC-Bayesian bounds inapplicable. We further refine existing bounds on the downstream classification loss by incorporating SimCLR-specific factors, including data augmentation and temperature scaling, and derive risk certificates for the contrastive zero-one risk. The resulting bounds for contrastive loss and downstream prediction are much tighter than those of previous risk certificates, as demonstrated by experiments on CIFAR-10.

Exact Certification of (Graph) Neural Networks Against Label Poisoning

Machine learning models are highly vulnerable to label flipping, i.e., the adversarial modification (poisoning) of training labels to compromise performance. Thus, deriving robustness certificates is important to guarantee that test predictions remain unaffected and to understand worst-case robustness behavior. However, for Graph Neural Networks (GNNs), the problem of certifying label flipping has so far been unsolved. We change this by introducing an exact certification method, deriving both sample-wise and collective certificates. Our method leverages the Neural Tangent Kernel (NTK) to capture the training dynamics of wide networks enabling us to reformulate the bilevel optimization problem representing label flipping into a Mixed-Integer Linear Program (MILP). We apply our method to certify a broad range of GNN architectures in node classification tasks. Thereby, concerning the worst-case robustness to label flipping: $(i)$ we establish hierarchies of GNNs on different benchmark graphs; $(ii)$ quantify the effect of architectural choices such as activations, depth and skip-connections; and surprisingly, $(iii)$ uncover a novel phenomenon of the robustness plateauing for intermediate perturbation budgets across all investigated datasets and architectures. While we focus on GNNs, our certificates are applicable to sufficiently wide NNs in general through their NTK. Thus, our work presents the first exact certificate to a poisoning attack ever derived for neural networks, which could be of independent interest.

Infinite Width Limits of Self Supervised Neural Networks

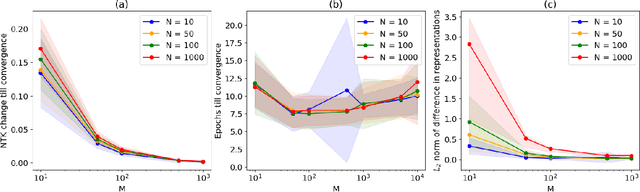
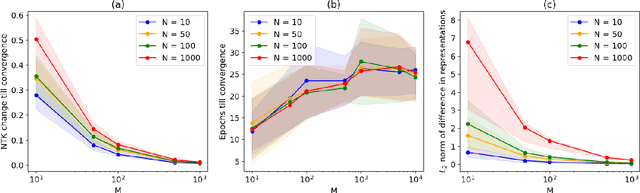
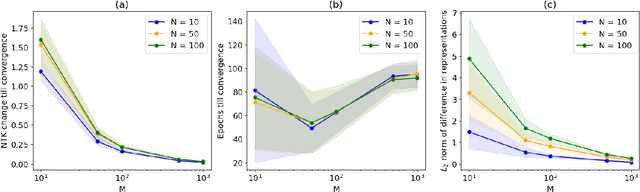
The NTK is a widely used tool in the theoretical analysis of deep learning, allowing us to look at supervised deep neural networks through the lenses of kernel regression. Recently, several works have investigated kernel models for self-supervised learning, hypothesizing that these also shed light on the behaviour of wide neural networks by virtue of the NTK. However, it remains an open question to what extent this connection is mathematically sound -- it is a commonly encountered misbelief that the kernel behaviour of wide neural networks emerges irrespective of the loss function it is trained on. In this paper, we bridge the gap between the NTK and self-supervised learning, focusing on two-layer neural networks trained under the Barlow Twins loss. We prove that the NTK of Barlow Twins indeed becomes constant as the width of the network approaches infinity. Our analysis technique is different from previous works on the NTK and may be of independent interest. Overall, our work provides a first rigorous justification for the use of classic kernel theory to understand self-supervised learning of wide neural networks. Building on this result, we derive generalization error bounds for kernelized Barlow Twins and connect them to neural networks of finite width.

Data Augmentations Go Beyond Encoding Invariances: A Theoretical Study on Self-Supervised Learning

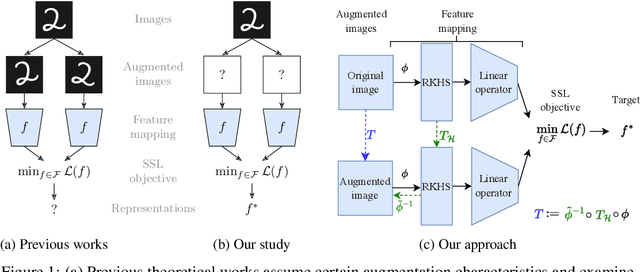
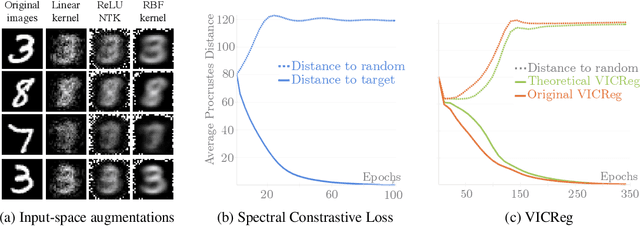
Understanding the role of data augmentations is critical for applying Self-Supervised Learning (SSL) methods in new domains. Data augmentations are commonly understood as encoding invariances into the learned representations. This interpretation suggests that SSL would require diverse augmentations that resemble the original data. However, in practice, augmentations do not need to be similar to the original data nor be diverse, and can be neither at the same time. We provide a theoretical insight into this phenomenon. We show that for different SSL losses, any non-redundant representation can be learned with a single suitable augmentation. We provide an algorithm to reconstruct such augmentations and give insights into augmentation choices in SSL.

Decision Trees for Interpretable Clusters in Mixture Models and Deep Representations

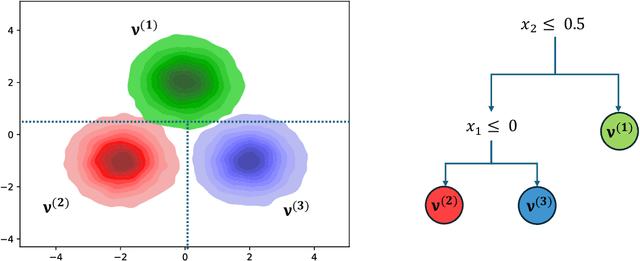
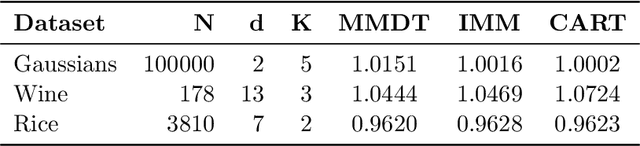
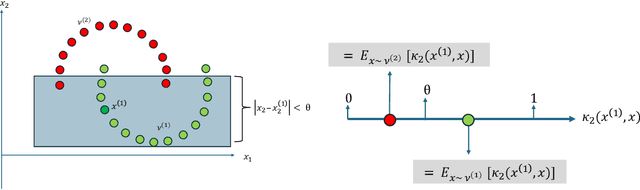
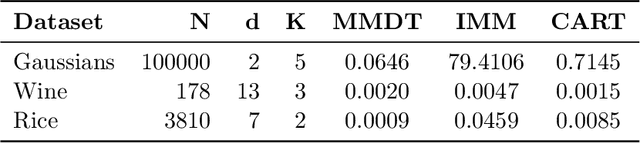
Decision Trees are one of the backbones of explainable machine learning, and often serve as interpretable alternatives to black-box models. Traditionally utilized in the supervised setting, there has recently also been a surge of interest in decision trees for unsupervised learning. While several works with worst-case guarantees on the clustering cost have appeared, these results are distribution-agnostic, and do not give insight into when decision trees can actually recover the underlying distribution of the data (up to some small error). In this paper, we therefore introduce the notion of an explainability-to-noise ratio for mixture models, formalizing the intuition that well-clustered data can indeed be explained well using a decision tree. We propose an algorithm that takes as input a mixture model and constructs a suitable tree in data-independent time. Assuming sub-Gaussianity of the mixture components, we prove upper and lower bounds on the error rate of the resulting decision tree. In addition, we demonstrate how concept activation vectors can be used to extend explainable clustering to neural networks. We empirically demonstrate the efficacy of our approach on standard tabular and image datasets.

Provable Robustness of (Graph) Neural Networks Against Data Poisoning and Backdoor Attacks

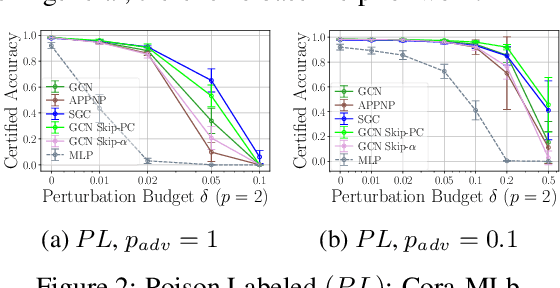
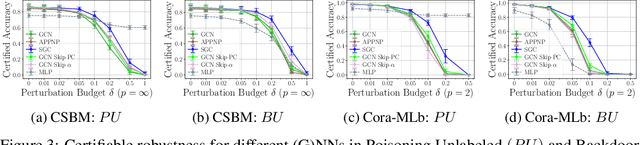
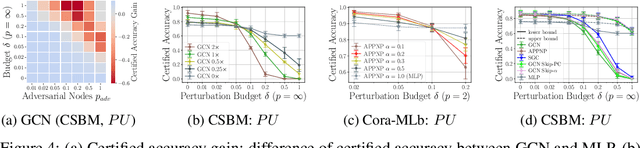
Generalization of machine learning models can be severely compromised by data poisoning, where adversarial changes are applied to the training data, as well as backdoor attacks that additionally manipulate the test data. These vulnerabilities have led to interest in certifying (i.e., proving) that such changes up to a certain magnitude do not affect test predictions. We, for the first time, certify Graph Neural Networks (GNNs) against poisoning and backdoor attacks targeting the node features of a given graph. Our certificates are white-box and based upon $(i)$ the neural tangent kernel, which characterizes the training dynamics of sufficiently wide networks; and $(ii)$ a novel reformulation of the bilevel optimization problem describing poisoning as a mixed-integer linear program. Consequently, we leverage our framework to provide fundamental insights into the role of graph structure and its connectivity on the worst-case robustness behavior of convolution-based and PageRank-based GNNs. We note that our framework is more general and constitutes the first approach to derive white-box poisoning certificates for NNs, which can be of independent interest beyond graph-related tasks.