Asynchronous Gossip Algorithms for Rank-Based Statistical Methods

As decentralized AI and edge intelligence become increasingly prevalent, ensuring robustness and trustworthiness in such distributed settings has become a critical issue-especially in the presence of corrupted or adversarial data. Traditional decentralized algorithms are vulnerable to data contamination as they typically rely on simple statistics (e.g., means or sum), motivating the need for more robust statistics. In line with recent work on decentralized estimation of trimmed means and ranks, we develop gossip algorithms for computing a broad class of rank-based statistics, including L-statistics and rank statistics-both known for their robustness to outliers. We apply our method to perform robust distributed two-sample hypothesis testing, introducing the first gossip algorithm for Wilcoxon rank-sum tests. We provide rigorous convergence guarantees, including the first convergence rate bound for asynchronous gossip-based rank estimation. We empirically validate our theoretical results through experiments on diverse network topologies.

Robust Distributed Estimation: Extending Gossip Algorithms to Ranking and Trimmed Means

This paper addresses the problem of robust estimation in gossip algorithms over arbitrary communication graphs. Gossip algorithms are fully decentralized, relying only on local neighbor-to-neighbor communication, making them well-suited for situations where communication is constrained. A fundamental challenge in existing mean-based gossip algorithms is their vulnerability to malicious or corrupted nodes. In this paper, we show that an outlier-robust mean can be computed by globally estimating a robust statistic. More specifically, we propose a novel gossip algorithm for rank estimation, referred to as \textsc{GoRank}, and leverage it to design a gossip procedure dedicated to trimmed mean estimation, coined \textsc{GoTrim}. In addition to a detailed description of the proposed methods, a key contribution of our work is a precise convergence analysis: we establish an $\mathcal{O}(1/t)$ rate for rank estimation and an $\mathcal{O}(\log(t)/t)$ rate for trimmed mean estimation, where by $t$ is meant the number of iterations. Moreover, we provide a breakdown point analysis of \textsc{GoTrim}. We empirically validate our theoretical results through experiments on diverse network topologies, data distributions and contamination schemes.

Tight PAC-Bayesian Risk Certificates for Contrastive Learning

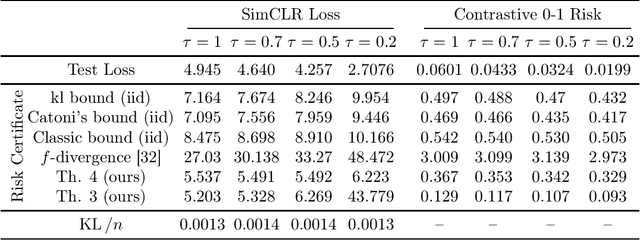
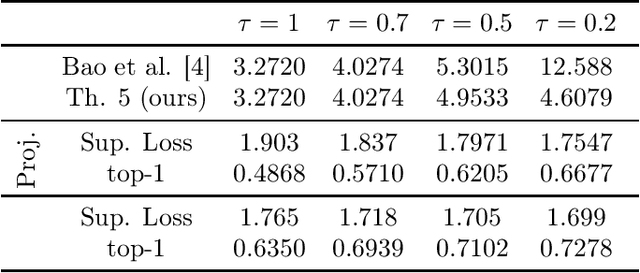
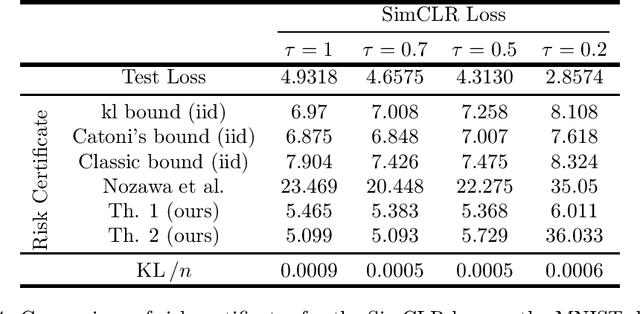
Contrastive representation learning is a modern paradigm for learning representations of unlabeled data via augmentations -- precisely, contrastive models learn to embed semantically similar pairs of samples (positive pairs) closer than independently drawn samples (negative samples). In spite of its empirical success and widespread use in foundation models, statistical theory for contrastive learning remains less explored. Recent works have developed generalization error bounds for contrastive losses, but the resulting risk certificates are either vacuous (certificates based on Rademacher complexity or $f$-divergence) or require strong assumptions about samples that are unreasonable in practice. The present paper develops non-vacuous PAC-Bayesian risk certificates for contrastive representation learning, considering the practical considerations of the popular SimCLR framework. Notably, we take into account that SimCLR reuses positive pairs of augmented data as negative samples for other data, thereby inducing strong dependence and making classical PAC or PAC-Bayesian bounds inapplicable. We further refine existing bounds on the downstream classification loss by incorporating SimCLR-specific factors, including data augmentation and temperature scaling, and derive risk certificates for the contrastive zero-one risk. The resulting bounds for contrastive loss and downstream prediction are much tighter than those of previous risk certificates, as demonstrated by experiments on CIFAR-10.