Flexible Parametric Inference for Space-Time Hawkes Processes

Many modern spatio-temporal data sets, in sociology, epidemiology or seismology, for example, exhibit self-exciting characteristics, triggering and clustering behaviors both at the same time, that a suitable Hawkes space-time process can accurately capture. This paper aims to develop a fast and flexible parametric inference technique to recover the parameters of the kernel functions involved in the intensity function of a space-time Hawkes process based on such data. Our statistical approach combines three key ingredients: 1) kernels with finite support are considered, 2) the space-time domain is appropriately discretized, and 3) (approximate) precomputations are used. The inference technique we propose then consists of a $\ell_2$ gradient-based solver that is fast and statistically accurate. In addition to describing the algorithmic aspects, numerical experiments have been carried out on synthetic and real spatio-temporal data, providing solid empirical evidence of the relevance of the proposed methodology.

Regular Variation in Hilbert Spaces and Principal Component Analysis for Functional Extremes

Motivated by the increasing availability of data of functional nature, we develop a general probabilistic and statistical framework for extremes of regularly varying random elements $X$ in $L^2[0,1]$. We place ourselves in a Peaks-Over-Threshold framework where a functional extreme is defined as an observation $X$ whose $L^2$-norm $\|X\|$ is comparatively large. Our goal is to propose a dimension reduction framework resulting into finite dimensional projections for such extreme observations. Our contribution is double. First, we investigate the notion of Regular Variation for random quantities valued in a general separable Hilbert space, for which we propose a novel concrete characterization involving solely stochastic convergence of real-valued random variables. Second, we propose a notion of functional Principal Component Analysis (PCA) accounting for the principal `directions' of functional extremes. We investigate the statistical properties of the empirical covariance operator of the angular component of extreme functions, by upper-bounding the Hilbert-Schmidt norm of the estimation error for finite sample sizes. Numerical experiments with simulated and real data illustrate this work.

On Regression in Extreme Regions

In the classic regression problem, the value of a real-valued random variable $Y$ is to be predicted based on the observation of a random vector $X$, taking its values in $\mathbb{R}^d$ with $d\geq 1$ say. The statistical learning problem consists in building a predictive function $\hat{f}:\mathbb{R}^d\to \mathbb{R}$ based on independent copies of the pair $(X,Y)$ so that $Y$ is approximated by $\hat{f}(X)$ with minimum error in the mean-squared sense. Motivated by various applications, ranging from environmental sciences to finance or insurance, special attention is paid here to the case of extreme (i.e. very large) observations $X$. Because of their rarity, they contribute in a negligible manner to the (empirical) error and the predictive performance of empirical quadratic risk minimizers can be consequently very poor in extreme regions. In this paper, we develop a general framework for regression in the extremes. It is assumed that $X$'s conditional distribution given $Y$ belongs to a non parametric class of heavy-tailed probability distributions. It is then shown that an asymptotic notion of risk can be tailored to summarize appropriately predictive performance in extreme regions of the input space. It is also proved that minimization of an empirical and non asymptotic version of this 'extreme risk', based on a fraction of the largest observations solely, yields regression functions with good generalization capacity. In addition, numerical results providing strong empirical evidence of the relevance of the approach proposed are displayed.

On Medians of (Randomized) Pairwise Means

Tournament procedures, recently introduced in Lugosi & Mendelson (2016), offer an appealing alternative, from a theoretical perspective at least, to the principle of Empirical Risk Minimization in machine learning. Statistical learning by Median-of-Means (MoM) basically consists in segmenting the training data into blocks of equal size and comparing the statistical performance of every pair of candidate decision rules on each data block: that with highest performance on the majority of the blocks is declared as the winner. In the context of nonparametric regression, functions having won all their duels have been shown to outperform empirical risk minimizers w.r.t. the mean squared error under minimal assumptions, while exhibiting robustness properties. It is the purpose of this paper to extend this approach in order to address other learning problems, in particular for which the performance criterion takes the form of an expectation over pairs of observations rather than over one single observation, as may be the case in pairwise ranking, clustering or metric learning. Precisely, it is proved here that the bounds achieved by MoM are essentially conserved when the blocks are built by means of independent sampling without replacement schemes instead of a simple segmentation. These results are next extended to situations where the risk is related to a pairwise loss function and its empirical counterpart is of the form of a $U$-statistic. Beyond theoretical results guaranteeing the performance of the learning/estimation methods proposed, some numerical experiments provide empirical evidence of their relevance in practice.

A Statistical Learning View of Simple Kriging

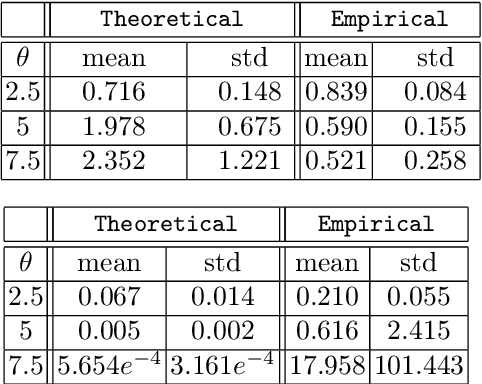
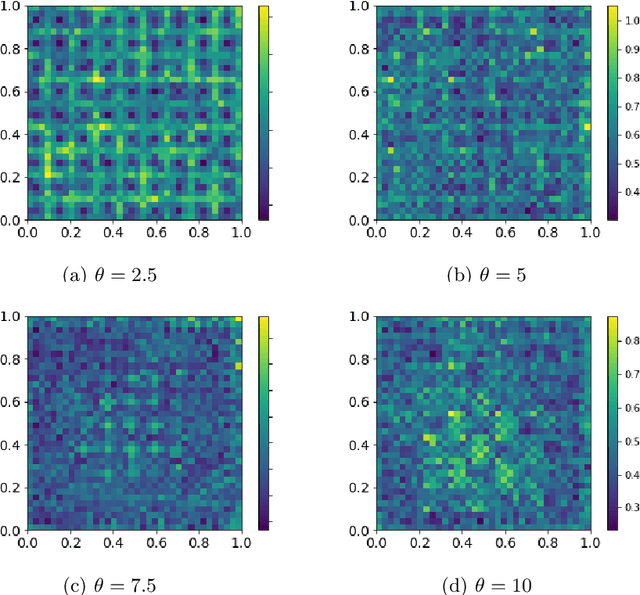
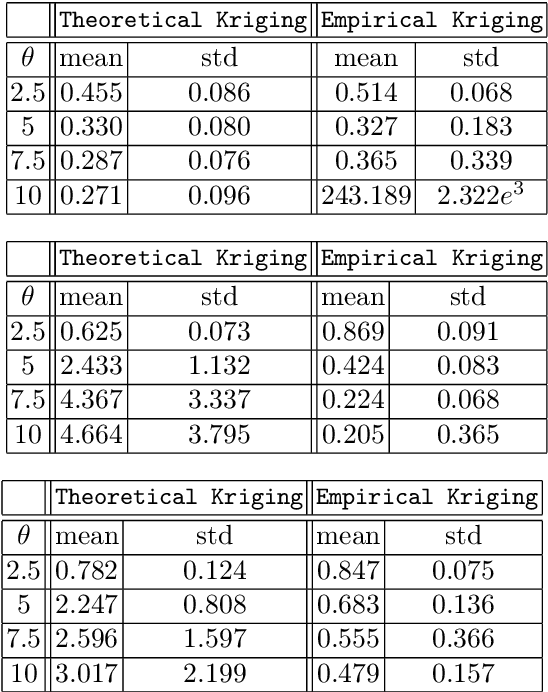
In the Big Data era, with the ubiquity of geolocation sensors in particular, massive datasets exhibiting a possibly complex spatial dependence structure are becoming increasingly available. In this context, the standard probabilistic theory of statistical learning does not apply directly and guarantees of the generalization capacity of predictive rules learned from such data are left to establish. We analyze here the simple Kriging task, the flagship problem in Geostatistics: the values of a square integrable random field $X=\{X_s\}_{s\in S}$, $S\subset \mathbb{R}^2$, with unknown covariance structure are to be predicted with minimum quadratic risk, based upon observing a single realization of the spatial process at a finite number of locations $s_1,\; \ldots,\; s_n$ in $S$. Despite the connection of this minimization problem with kernel ridge regression, establishing the generalization capacity of empirical risk minimizers is far from straightforward, due to the non i.i.d. nature of the spatial data $X_{s_1},\; \ldots,\; X_{s_n}$ involved. In this article, nonasymptotic bounds of order $O_{\mathbb{P}}(1/n)$ are proved for the excess risk of a plug-in predictive rule mimicking the true minimizer in the case of isotropic stationary Gaussian processes observed at locations forming a regular grid. These theoretical results, as well as the role played by the technical conditions required to establish them, are illustrated by various numerical experiments and hopefully pave the way for further developments in statistical learning based on spatial data.

Improving the quality control of seismic data through active learning

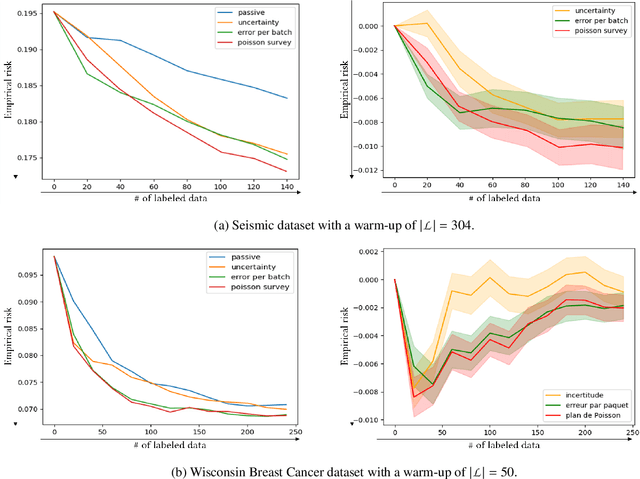
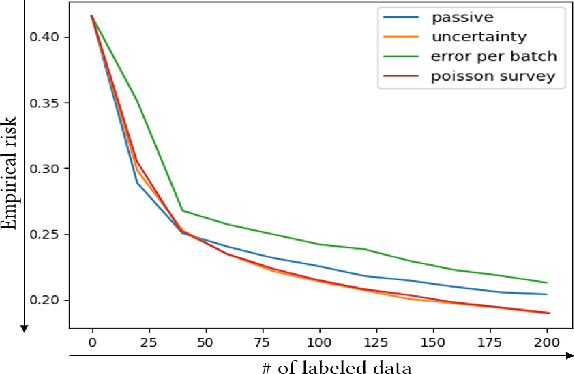
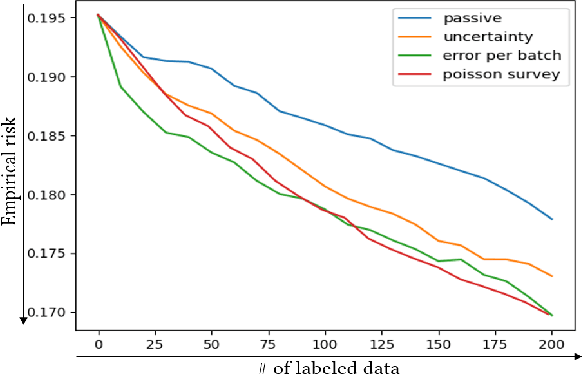
In image denoising problems, the increasing density of available images makes an exhaustive visual inspection impossible and therefore automated methods based on machine-learning must be deployed for this purpose. This is particulary the case in seismic signal processing. Engineers/geophysicists have to deal with millions of seismic time series. Finding the sub-surface properties useful for the oil industry may take up to a year and is very costly in terms of computing/human resources. In particular, the data must go through different steps of noise attenuation. Each denoise step is then ideally followed by a quality control (QC) stage performed by means of human expertise. To learn a quality control classifier in a supervised manner, labeled training data must be available, but collecting the labels from human experts is extremely time-consuming. We therefore propose a novel active learning methodology to sequentially select the most relevant data, which are then given back to a human expert for labeling. Beyond the application in geophysics, the technique we promote in this paper, based on estimates of the local error and its uncertainty, is generic. Its performance is supported by strong empirical evidence, as illustrated by the numerical experiments presented in this article, where it is compared to alternative active learning strategies both on synthetic and real seismic datasets.

Functional Anomaly Detection: a Benchmark Study

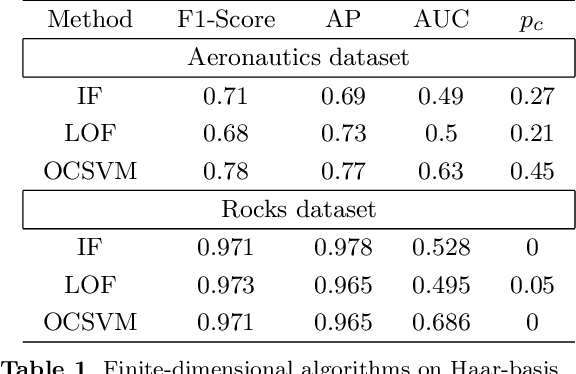
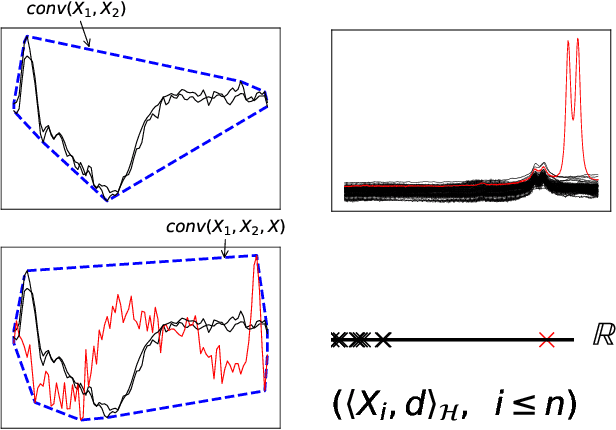
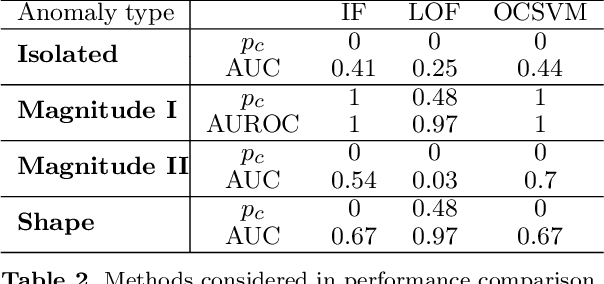
The increasing automation in many areas of the Industry expressly demands to design efficient machine-learning solutions for the detection of abnormal events. With the ubiquitous deployment of sensors monitoring nearly continuously the health of complex infrastructures, anomaly detection can now rely on measurements sampled at a very high frequency, providing a very rich representation of the phenomenon under surveillance. In order to exploit fully the information thus collected, the observations cannot be treated as multivariate data anymore and a functional analysis approach is required. It is the purpose of this paper to investigate the performance of recent techniques for anomaly detection in the functional setup on real datasets. After an overview of the state-of-the-art and a visual-descriptive study, a variety of anomaly detection methods are compared. While taxonomies of abnormalities (e.g. shape, location) in the functional setup are documented in the literature, assigning a specific type to the identified anomalies appears to be a challenging task. Thus, strengths and weaknesses of the existing approaches are benchmarked in view of these highlighted types in a simulation study. Anomaly detection methods are next evaluated on two datasets, related to the monitoring of helicopters in flight and to the spectrometry of construction materials namely. The benchmark analysis is concluded by recommendation guidance for practitioners.

Visual Recognition with Deep Learning from Biased Image Datasets

In practice, and more especially when training deep neural networks, visual recognition rules are often learned based on various sources of information. On the other hand, the recent deployment of facial recognition systems with uneven predictive performances on different population segments highlights the representativeness issues possibly induced by a naive aggregation of image datasets. Indeed, sampling bias does not vanish simply by considering larger datasets, and ignoring its impact may completely jeopardize the generalization capacity of the learned prediction rules. In this paper, we show how biasing models, originally introduced for nonparametric estimation in (Gill et al., 1988), and recently revisited from the perspective of statistical learning theory in (Laforgue and Cl\'emen\c{c}on, 2019), can be applied to remedy these problems in the context of visual recognition. Based on the (approximate) knowledge of the biasing mechanisms at work, our approach consists in reweighting the observations, so as to form a nearly debiased estimator of the target distribution. One key condition for our method to be theoretically valid is that the supports of the distributions generating the biased datasets at disposal must overlap, and cover the support of the target distribution. In order to meet this requirement in practice, we propose to use a low dimensional image representation, shared across the image databases. Finally, we provide numerical experiments highlighting the relevance of our approach whenever the biasing functions are appropriately chosen.

Individual Survival Curves with Conditional Normalizing Flows

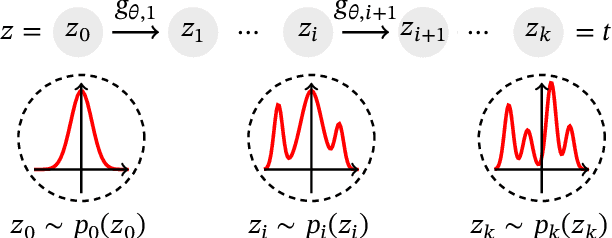
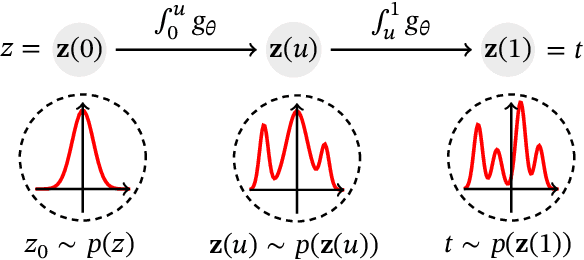
Survival analysis, or time-to-event modelling, is a classical statistical problem that has garnered a lot of interest for its practical use in epidemiology, demographics or actuarial sciences. Recent advances on the subject from the point of view of machine learning have been concerned with precise per-individual predictions instead of population studies, driven by the rise of individualized medicine. We introduce here a conditional normalizing flow based estimate of the time-to-event density as a way to model highly flexible and individualized conditional survival distributions. We use a novel hierarchical formulation of normalizing flows to enable efficient fitting of flexible conditional distributions without overfitting and show how the normalizing flow formulation can be efficiently adapted to the censored setting. We experimentally validate the proposed approach on a synthetic dataset as well as four open medical datasets and an example of a common financial problem.

Nearest Neighbour Based Estimates of Gradients: Sharp Nonasymptotic Bounds and Applications

Motivated by a wide variety of applications, ranging from stochastic optimization to dimension reduction through variable selection, the problem of estimating gradients accurately is of crucial importance in statistics and learning theory. We consider here the classic regression setup, where a real valued square integrable r.v. $Y$ is to be predicted upon observing a (possibly high dimensional) random vector $X$ by means of a predictive function $f(X)$ as accurately as possible in the mean-squared sense and study a nearest-neighbour-based pointwise estimate of the gradient of the optimal predictive function, the regression function $m(x)=\mathbb{E}[Y\mid X=x]$. Under classic smoothness conditions combined with the assumption that the tails of $Y-m(X)$ are sub-Gaussian, we prove nonasymptotic bounds improving upon those obtained for alternative estimation methods. Beyond the novel theoretical results established, several illustrative numerical experiments have been carried out. The latter provide strong empirical evidence that the estimation method proposed works very well for various statistical problems involving gradient estimation, namely dimensionality reduction, stochastic gradient descent optimization and quantifying disentanglement.