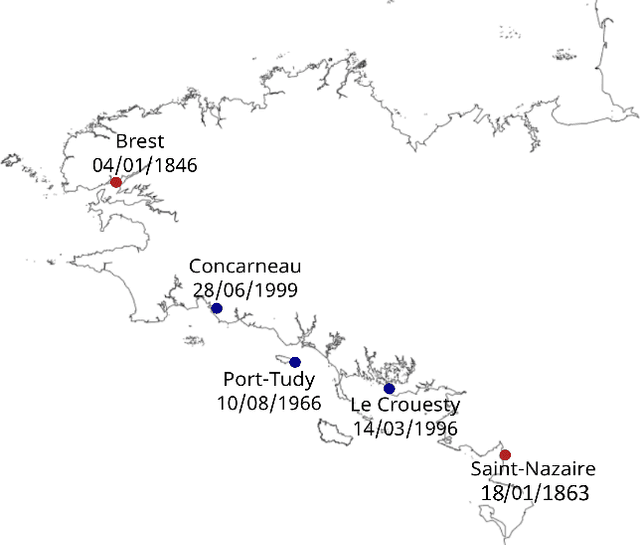
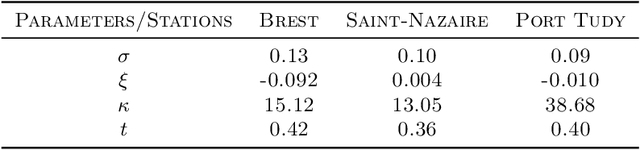
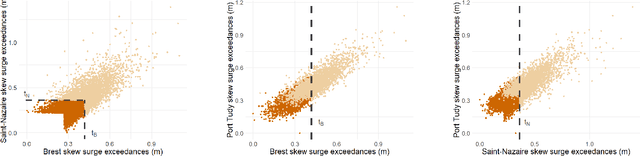
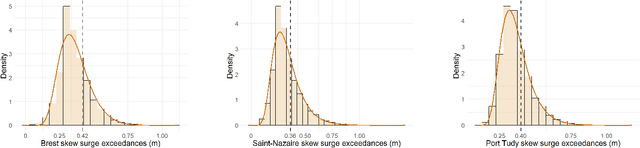
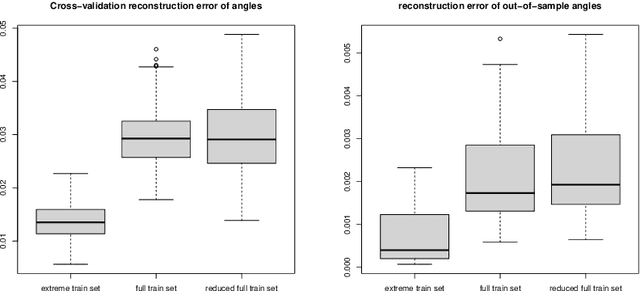
Multi-site modelling and reconstruction of past extreme skew surges along the French Atlantic coast

Appropriate modelling of extreme skew surges is crucial, particularly for coastal risk management. Our study focuses on modelling extreme skew surges along the French Atlantic coast, with a particular emphasis on investigating the extremal dependence structure between stations. We employ the peak-over-threshold framework, where a multivariate extreme event is defined whenever at least one location records a large value, though not necessarily all stations simultaneously. A novel method for determining an appropriate level (threshold) above which observations can be classified as extreme is proposed. Two complementary approaches are explored. First, the multivariate generalized Pareto distribution is employed to model extremes, leveraging its properties to derive a generative model that predicts extreme skew surges at one station based on observed extremes at nearby stations. Second, a novel extreme regression framework is assessed for point predictions. This specific regression framework enables accurate point predictions using only the "angle" of input variables, i.e. input variables divided by their norms. The ultimate objective is to reconstruct historical skew surge time series at stations with limited data. This is achieved by integrating extreme skew surge data from stations with longer records, such as Brest and Saint-Nazaire, which provide over 150 years of observations.

Regular Variation in Hilbert Spaces and Principal Component Analysis for Functional Extremes

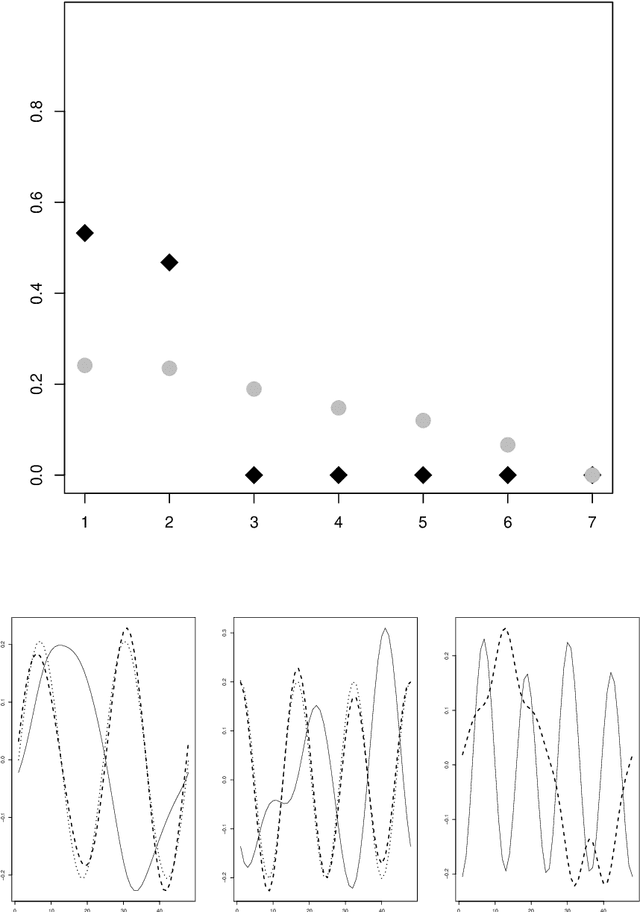
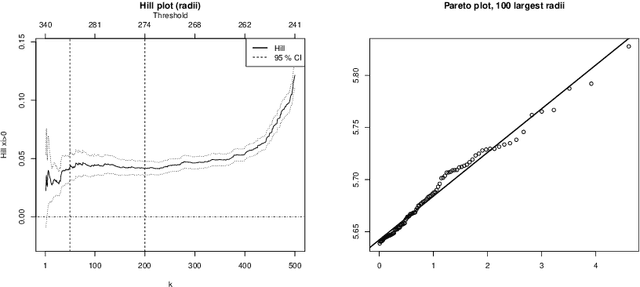
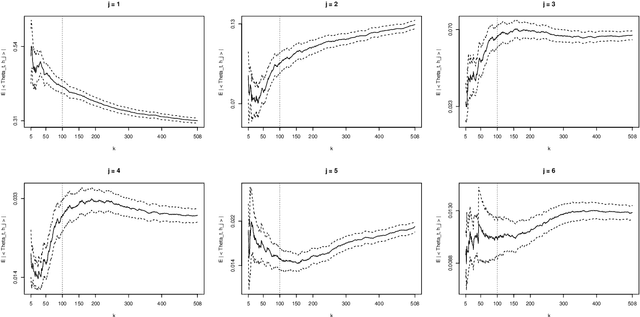
Motivated by the increasing availability of data of functional nature, we develop a general probabilistic and statistical framework for extremes of regularly varying random elements $X$ in $L^2[0,1]$. We place ourselves in a Peaks-Over-Threshold framework where a functional extreme is defined as an observation $X$ whose $L^2$-norm $\|X\|$ is comparatively large. Our goal is to propose a dimension reduction framework resulting into finite dimensional projections for such extreme observations. Our contribution is double. First, we investigate the notion of Regular Variation for random quantities valued in a general separable Hilbert space, for which we propose a novel concrete characterization involving solely stochastic convergence of real-valued random variables. Second, we propose a notion of functional Principal Component Analysis (PCA) accounting for the principal `directions' of functional extremes. We investigate the statistical properties of the empirical covariance operator of the angular component of extreme functions, by upper-bounding the Hilbert-Schmidt norm of the estimation error for finite sample sizes. Numerical experiments with simulated and real data illustrate this work.

On Regression in Extreme Regions

In the classic regression problem, the value of a real-valued random variable $Y$ is to be predicted based on the observation of a random vector $X$, taking its values in $\mathbb{R}^d$ with $d\geq 1$ say. The statistical learning problem consists in building a predictive function $\hat{f}:\mathbb{R}^d\to \mathbb{R}$ based on independent copies of the pair $(X,Y)$ so that $Y$ is approximated by $\hat{f}(X)$ with minimum error in the mean-squared sense. Motivated by various applications, ranging from environmental sciences to finance or insurance, special attention is paid here to the case of extreme (i.e. very large) observations $X$. Because of their rarity, they contribute in a negligible manner to the (empirical) error and the predictive performance of empirical quadratic risk minimizers can be consequently very poor in extreme regions. In this paper, we develop a general framework for regression in the extremes. It is assumed that $X$'s conditional distribution given $Y$ belongs to a non parametric class of heavy-tailed probability distributions. It is then shown that an asymptotic notion of risk can be tailored to summarize appropriately predictive performance in extreme regions of the input space. It is also proved that minimization of an empirical and non asymptotic version of this 'extreme risk', based on a fraction of the largest observations solely, yields regression functions with good generalization capacity. In addition, numerical results providing strong empirical evidence of the relevance of the approach proposed are displayed.