Flexible Parametric Inference for Space-Time Hawkes Processes

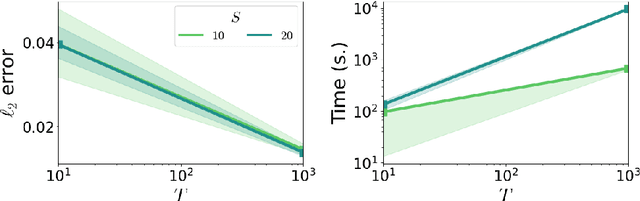
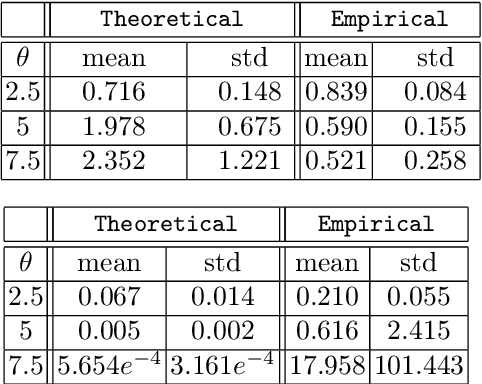
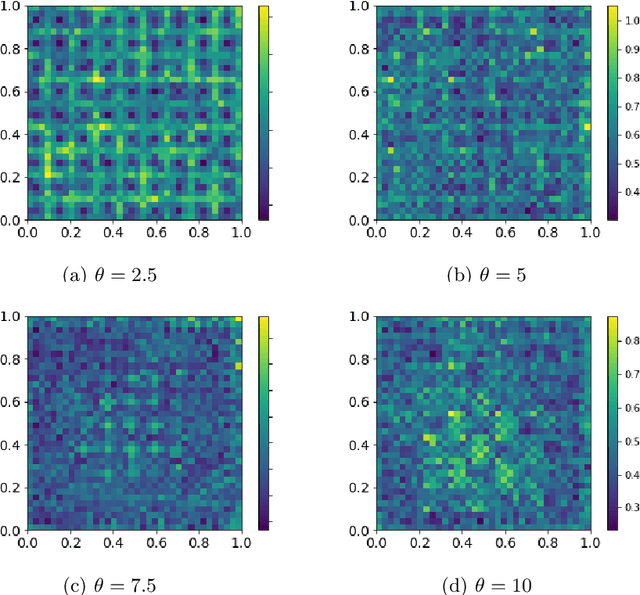
Many modern spatio-temporal data sets, in sociology, epidemiology or seismology, for example, exhibit self-exciting characteristics, triggering and clustering behaviors both at the same time, that a suitable Hawkes space-time process can accurately capture. This paper aims to develop a fast and flexible parametric inference technique to recover the parameters of the kernel functions involved in the intensity function of a space-time Hawkes process based on such data. Our statistical approach combines three key ingredients: 1) kernels with finite support are considered, 2) the space-time domain is appropriately discretized, and 3) (approximate) precomputations are used. The inference technique we propose then consists of a $\ell_2$ gradient-based solver that is fast and statistically accurate. In addition to describing the algorithmic aspects, numerical experiments have been carried out on synthetic and real spatio-temporal data, providing solid empirical evidence of the relevance of the proposed methodology.

A Statistical Learning View of Simple Kriging

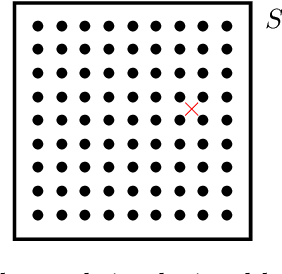
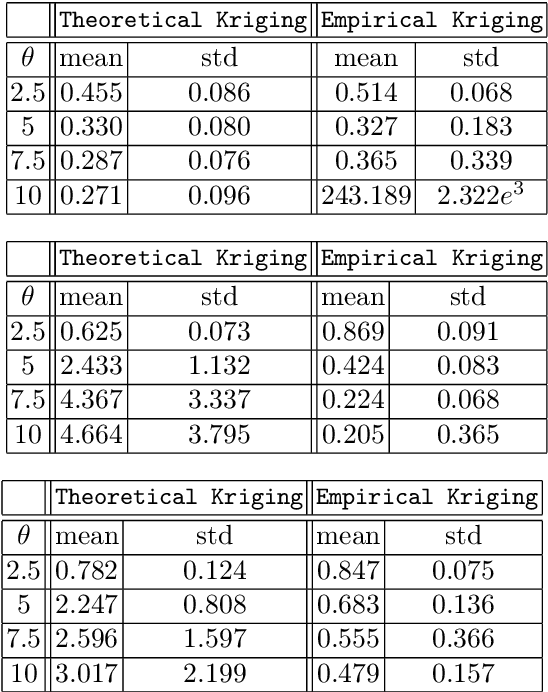
In the Big Data era, with the ubiquity of geolocation sensors in particular, massive datasets exhibiting a possibly complex spatial dependence structure are becoming increasingly available. In this context, the standard probabilistic theory of statistical learning does not apply directly and guarantees of the generalization capacity of predictive rules learned from such data are left to establish. We analyze here the simple Kriging task, the flagship problem in Geostatistics: the values of a square integrable random field $X=\{X_s\}_{s\in S}$, $S\subset \mathbb{R}^2$, with unknown covariance structure are to be predicted with minimum quadratic risk, based upon observing a single realization of the spatial process at a finite number of locations $s_1,\; \ldots,\; s_n$ in $S$. Despite the connection of this minimization problem with kernel ridge regression, establishing the generalization capacity of empirical risk minimizers is far from straightforward, due to the non i.i.d. nature of the spatial data $X_{s_1},\; \ldots,\; X_{s_n}$ involved. In this article, nonasymptotic bounds of order $O_{\mathbb{P}}(1/n)$ are proved for the excess risk of a plug-in predictive rule mimicking the true minimizer in the case of isotropic stationary Gaussian processes observed at locations forming a regular grid. These theoretical results, as well as the role played by the technical conditions required to establish them, are illustrated by various numerical experiments and hopefully pave the way for further developments in statistical learning based on spatial data.