Flexible Parametric Inference for Space-Time Hawkes Processes
Paper and Code
Jun 10, 2024

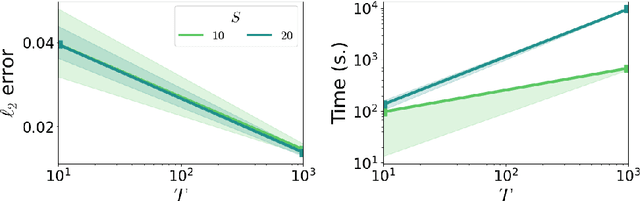

Many modern spatio-temporal data sets, in sociology, epidemiology or seismology, for example, exhibit self-exciting characteristics, triggering and clustering behaviors both at the same time, that a suitable Hawkes space-time process can accurately capture. This paper aims to develop a fast and flexible parametric inference technique to recover the parameters of the kernel functions involved in the intensity function of a space-time Hawkes process based on such data. Our statistical approach combines three key ingredients: 1) kernels with finite support are considered, 2) the space-time domain is appropriately discretized, and 3) (approximate) precomputations are used. The inference technique we propose then consists of a $\ell_2$ gradient-based solver that is fast and statistically accurate. In addition to describing the algorithmic aspects, numerical experiments have been carried out on synthetic and real spatio-temporal data, providing solid empirical evidence of the relevance of the proposed methodology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge