A Statistical Learning View of Simple Kriging

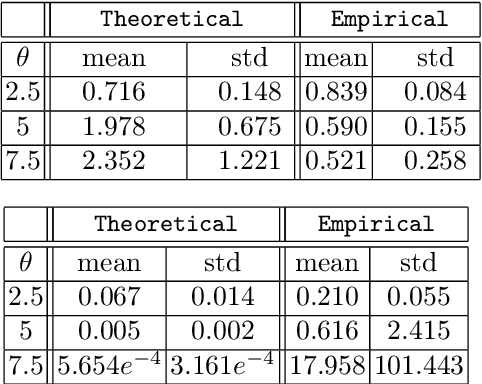
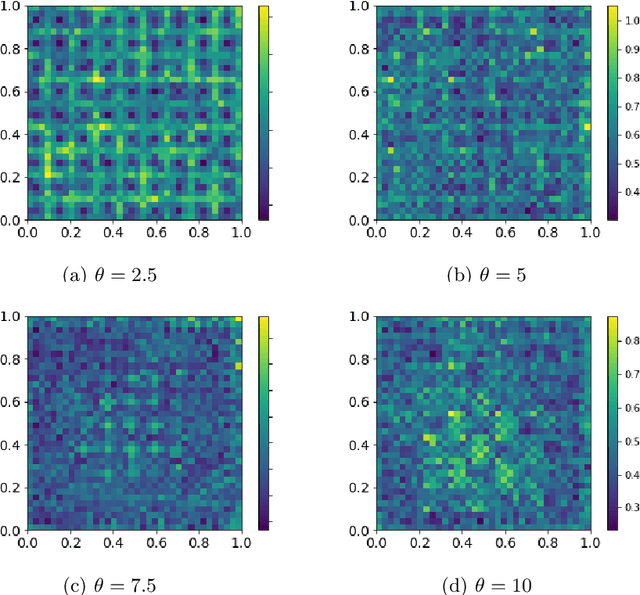
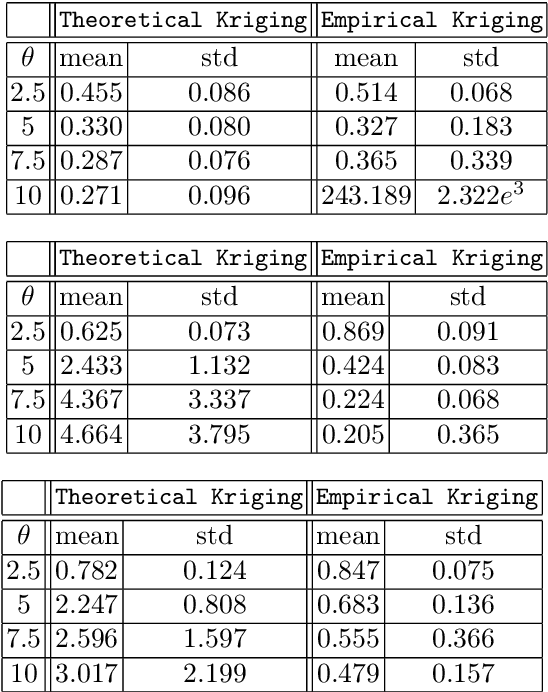
In the Big Data era, with the ubiquity of geolocation sensors in particular, massive datasets exhibiting a possibly complex spatial dependence structure are becoming increasingly available. In this context, the standard probabilistic theory of statistical learning does not apply directly and guarantees of the generalization capacity of predictive rules learned from such data are left to establish. We analyze here the simple Kriging task, the flagship problem in Geostatistics: the values of a square integrable random field $X=\{X_s\}_{s\in S}$, $S\subset \mathbb{R}^2$, with unknown covariance structure are to be predicted with minimum quadratic risk, based upon observing a single realization of the spatial process at a finite number of locations $s_1,\; \ldots,\; s_n$ in $S$. Despite the connection of this minimization problem with kernel ridge regression, establishing the generalization capacity of empirical risk minimizers is far from straightforward, due to the non i.i.d. nature of the spatial data $X_{s_1},\; \ldots,\; X_{s_n}$ involved. In this article, nonasymptotic bounds of order $O_{\mathbb{P}}(1/n)$ are proved for the excess risk of a plug-in predictive rule mimicking the true minimizer in the case of isotropic stationary Gaussian processes observed at locations forming a regular grid. These theoretical results, as well as the role played by the technical conditions required to establish them, are illustrated by various numerical experiments and hopefully pave the way for further developments in statistical learning based on spatial data.

Improving the quality control of seismic data through active learning

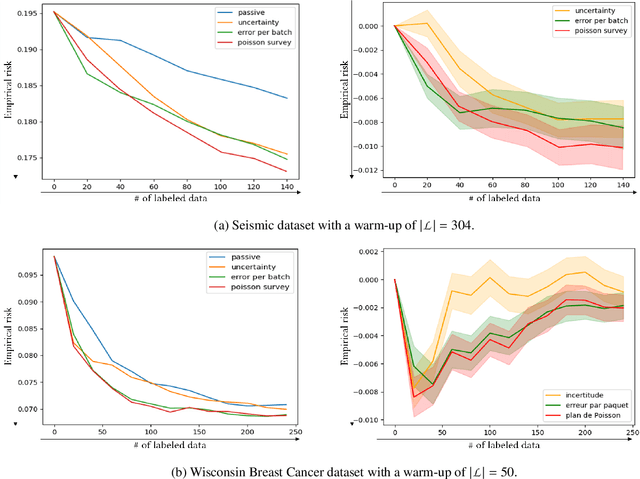
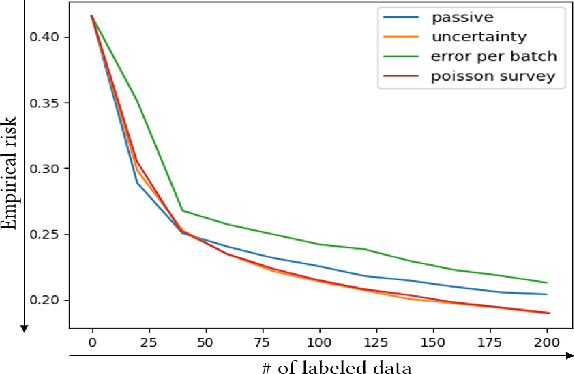
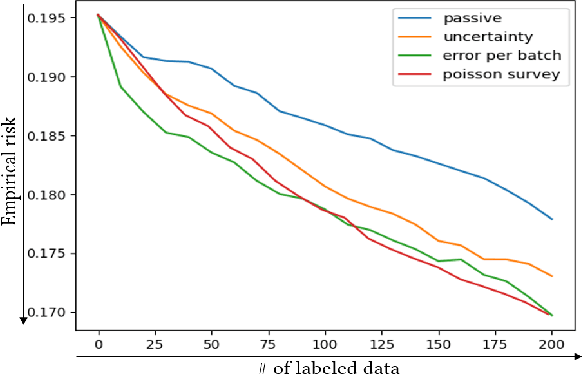
In image denoising problems, the increasing density of available images makes an exhaustive visual inspection impossible and therefore automated methods based on machine-learning must be deployed for this purpose. This is particulary the case in seismic signal processing. Engineers/geophysicists have to deal with millions of seismic time series. Finding the sub-surface properties useful for the oil industry may take up to a year and is very costly in terms of computing/human resources. In particular, the data must go through different steps of noise attenuation. Each denoise step is then ideally followed by a quality control (QC) stage performed by means of human expertise. To learn a quality control classifier in a supervised manner, labeled training data must be available, but collecting the labels from human experts is extremely time-consuming. We therefore propose a novel active learning methodology to sequentially select the most relevant data, which are then given back to a human expert for labeling. Beyond the application in geophysics, the technique we promote in this paper, based on estimates of the local error and its uncertainty, is generic. Its performance is supported by strong empirical evidence, as illustrated by the numerical experiments presented in this article, where it is compared to alternative active learning strategies both on synthetic and real seismic datasets.

Survey schemes for stochastic gradient descent with applications to M-estimation

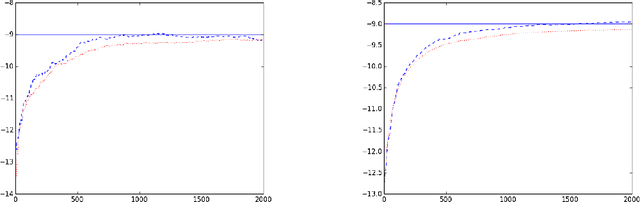
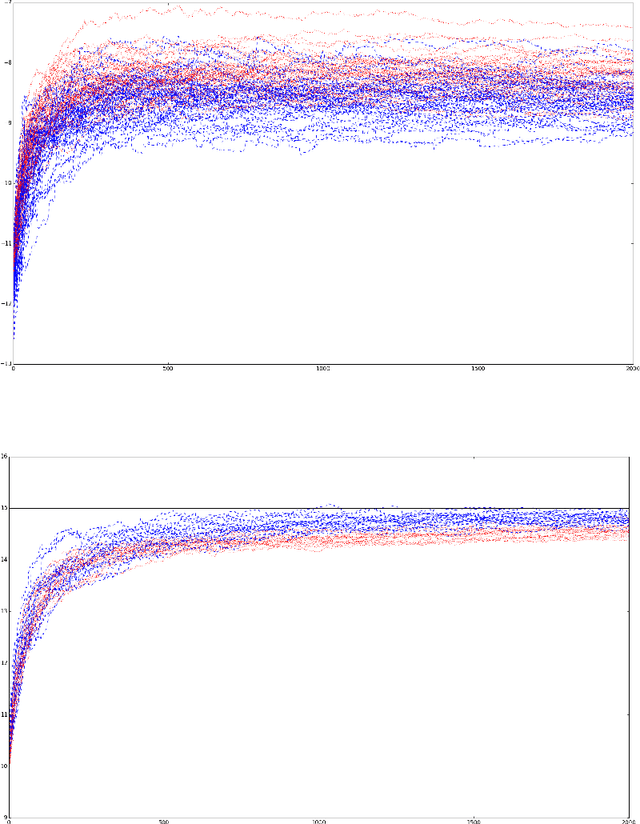
In certain situations that shall be undoubtedly more and more common in the Big Data era, the datasets available are so massive that computing statistics over the full sample is hardly feasible, if not unfeasible. A natural approach in this context consists in using survey schemes and substituting the "full data" statistics with their counterparts based on the resulting random samples, of manageable size. It is the main purpose of this paper to investigate the impact of survey sampling with unequal inclusion probabilities on stochastic gradient descent-based M-estimation methods in large-scale statistical and machine-learning problems. Precisely, we prove that, in presence of some a priori information, one may significantly increase asymptotic accuracy when choosing appropriate first order inclusion probabilities, without affecting complexity. These striking results are described here by limit theorems and are also illustrated by numerical experiments.