A Statistical Learning View of Simple Kriging
Paper and Code
Feb 18, 2022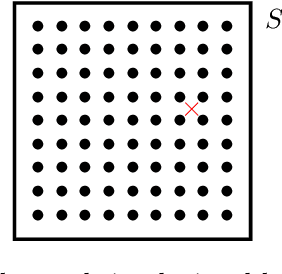
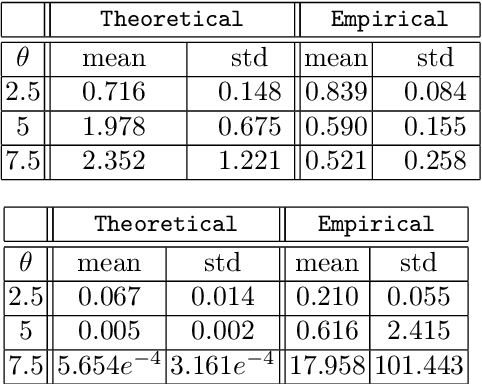
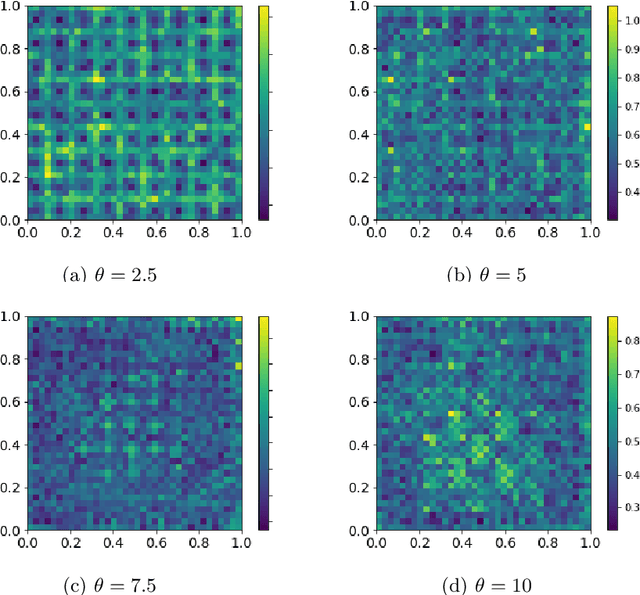
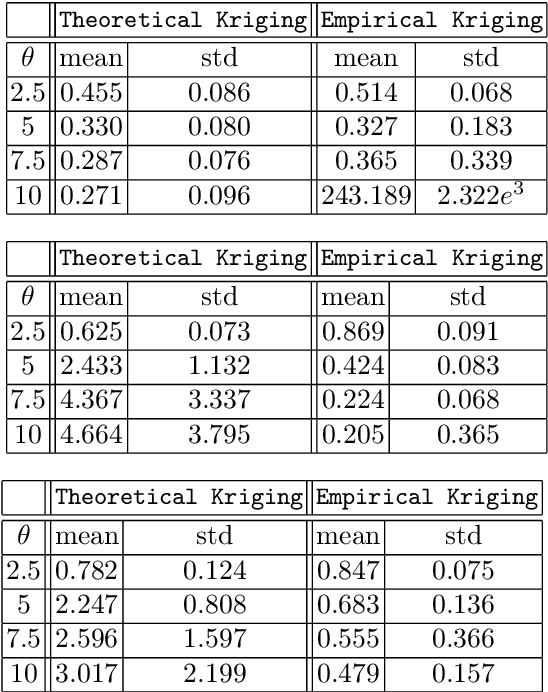
In the Big Data era, with the ubiquity of geolocation sensors in particular, massive datasets exhibiting a possibly complex spatial dependence structure are becoming increasingly available. In this context, the standard probabilistic theory of statistical learning does not apply directly and guarantees of the generalization capacity of predictive rules learned from such data are left to establish. We analyze here the simple Kriging task, the flagship problem in Geostatistics: the values of a square integrable random field $X=\{X_s\}_{s\in S}$, $S\subset \mathbb{R}^2$, with unknown covariance structure are to be predicted with minimum quadratic risk, based upon observing a single realization of the spatial process at a finite number of locations $s_1,\; \ldots,\; s_n$ in $S$. Despite the connection of this minimization problem with kernel ridge regression, establishing the generalization capacity of empirical risk minimizers is far from straightforward, due to the non i.i.d. nature of the spatial data $X_{s_1},\; \ldots,\; X_{s_n}$ involved. In this article, nonasymptotic bounds of order $O_{\mathbb{P}}(1/n)$ are proved for the excess risk of a plug-in predictive rule mimicking the true minimizer in the case of isotropic stationary Gaussian processes observed at locations forming a regular grid. These theoretical results, as well as the role played by the technical conditions required to establish them, are illustrated by various numerical experiments and hopefully pave the way for further developments in statistical learning based on spatial data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge