On Ranking-based Tests of Independence

In this paper we develop a novel nonparametric framework to test the independence of two random variables $\mathbf{X}$ and $\mathbf{Y}$ with unknown respective marginals $H(dx)$ and $G(dy)$ and joint distribution $F(dx dy)$, based on {\it Receiver Operating Characteristic} (ROC) analysis and bipartite ranking. The rationale behind our approach relies on the fact that, the independence hypothesis $\mathcal{H}\_0$ is necessarily false as soon as the optimal scoring function related to the pair of distributions $(H\otimes G,\; F)$, obtained from a bipartite ranking algorithm, has a ROC curve that deviates from the main diagonal of the unit square.We consider a wide class of rank statistics encompassing many ways of deviating from the diagonal in the ROC space to build tests of independence. Beyond its great flexibility, this new method has theoretical properties that far surpass those of its competitors. Nonasymptotic bounds for the two types of testing errors are established. From an empirical perspective, the novel procedure we promote in this paper exhibits a remarkable ability to detect small departures, of various types, from the null assumption $\mathcal{H}_0$, even in high dimension, as supported by the numerical experiments presented here.

Robust Consensus in Ranking Data Analysis: Definitions, Properties and Computational Issues

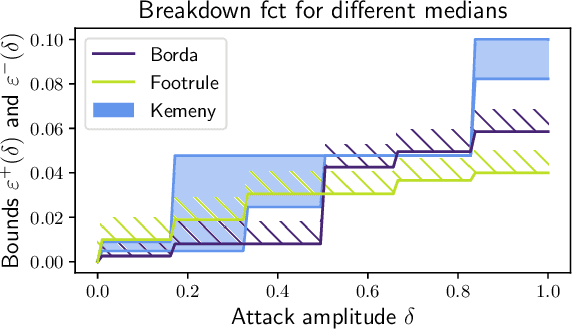
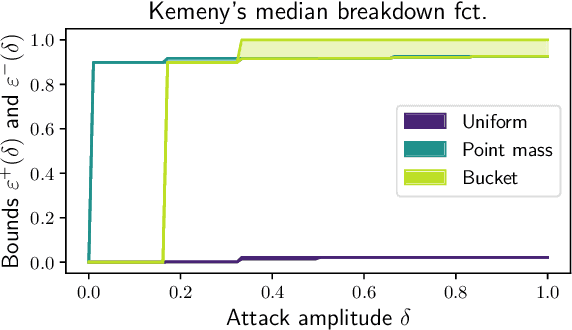
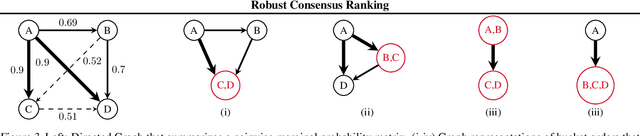
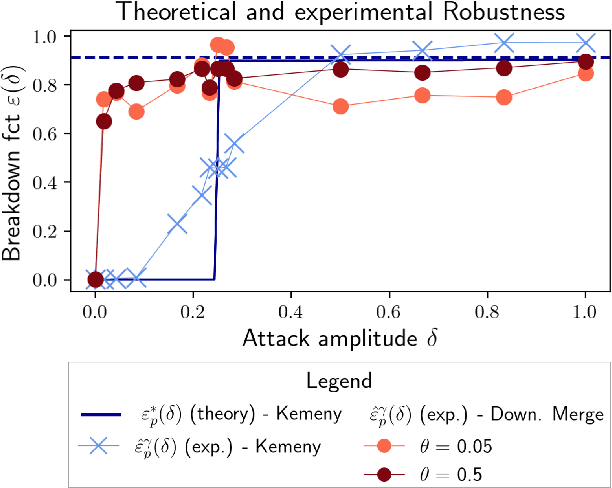
As the issue of robustness in AI systems becomes vital, statistical learning techniques that are reliable even in presence of partly contaminated data have to be developed. Preference data, in the form of (complete) rankings in the simplest situations, are no exception and the demand for appropriate concepts and tools is all the more pressing given that technologies fed by or producing this type of data (e.g. search engines, recommending systems) are now massively deployed. However, the lack of vector space structure for the set of rankings (i.e. the symmetric group $\mathfrak{S}_n$) and the complex nature of statistics considered in ranking data analysis make the formulation of robustness objectives in this domain challenging. In this paper, we introduce notions of robustness, together with dedicated statistical methods, for Consensus Ranking the flagship problem in ranking data analysis, aiming at summarizing a probability distribution on $\mathfrak{S}_n$ by a median ranking. Precisely, we propose specific extensions of the popular concept of breakdown point, tailored to consensus ranking, and address the related computational issues. Beyond the theoretical contributions, the relevance of the approach proposed is supported by an experimental study.

Assessing Performance and Fairness Metrics in Face Recognition - Bootstrap Methods

The ROC curve is the major tool for assessing not only the performance but also the fairness properties of a similarity scoring function in Face Recognition. In order to draw reliable conclusions based on empirical ROC analysis, evaluating accurately the uncertainty related to statistical versions of the ROC curves of interest is necessary. For this purpose, we explain in this paper that, because the True/False Acceptance Rates are of the form of U-statistics in the case of similarity scoring, the naive bootstrap approach is not valid here and that a dedicated recentering technique must be used instead. This is illustrated on real data of face images, when applied to several ROC-based metrics such as popular fairness metrics.

Mitigating Gender Bias in Face Recognition Using the von Mises-Fisher Mixture Model

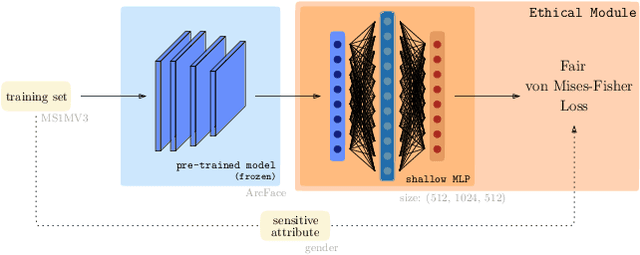
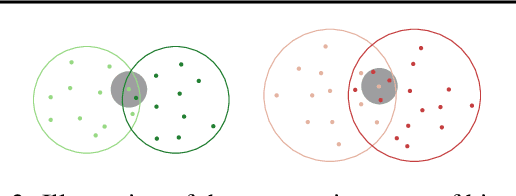
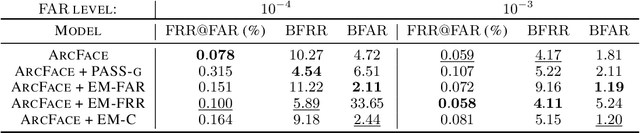
In spite of the high performance and reliability of deep learning algorithms in a wide range of everyday applications, many investigations tend to show that a lot of models exhibit biases, discriminating against specific subgroups of the population (e.g. gender, ethnicity). This urges the practitioner to develop fair systems with a uniform/comparable performance across sensitive groups. In this work, we investigate the gender bias of deep Face Recognition networks. In order to measure this bias, we introduce two new metrics, $\mathrm{BFAR}$ and $\mathrm{BFRR}$, that better reflect the inherent deployment needs of Face Recognition systems. Motivated by geometric considerations, we mitigate gender bias through a new post-processing methodology which transforms the deep embeddings of a pre-trained model to give more representation power to discriminated subgroups. It consists in training a shallow neural network by minimizing a Fair von Mises-Fisher loss whose hyperparameters account for the intra-class variance of each gender. Interestingly, we empirically observe that these hyperparameters are correlated with our fairness metrics. In fact, extensive numerical experiments on a variety of datasets show that a careful selection significantly reduces gender bias.

Statistical Depth Functions for Ranking Distributions: Definitions, Statistical Learning and Applications

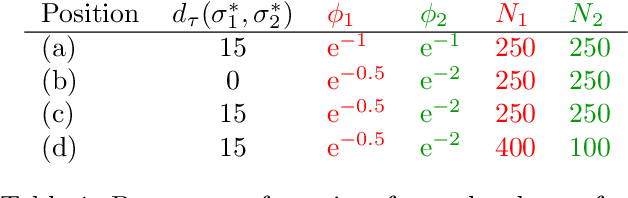
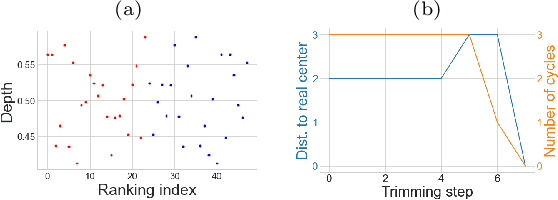
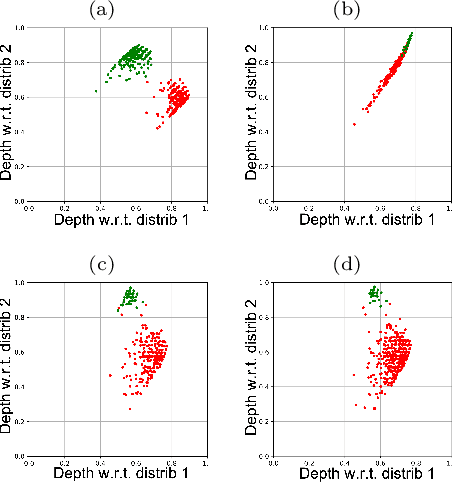
The concept of median/consensus has been widely investigated in order to provide a statistical summary of ranking data, i.e. realizations of a random permutation $\Sigma$ of a finite set, $\{1,\; \ldots,\; n\}$ with $n\geq 1$ say. As it sheds light onto only one aspect of $\Sigma$'s distribution $P$, it may neglect other informative features. It is the purpose of this paper to define analogs of quantiles, ranks and statistical procedures based on such quantities for the analysis of ranking data by means of a metric-based notion of depth function on the symmetric group. Overcoming the absence of vector space structure on $\mathfrak{S}_n$, the latter defines a center-outward ordering of the permutations in the support of $P$ and extends the classic metric-based formulation of consensus ranking (medians corresponding then to the deepest permutations). The axiomatic properties that ranking depths should ideally possess are listed, while computational and generalization issues are studied at length. Beyond the theoretical analysis carried out, the relevance of the novel concepts and methods introduced for a wide variety of statistical tasks are also supported by numerous numerical experiments.

Learning to Rank Anomalies: Scalar Performance Criteria and Maximization of Two-Sample Rank Statistics

The ability to collect and store ever more massive databases has been accompanied by the need to process them efficiently. In many cases, most observations have the same behavior, while a probable small proportion of these observations are abnormal. Detecting the latter, defined as outliers, is one of the major challenges for machine learning applications (e.g. in fraud detection or in predictive maintenance). In this paper, we propose a methodology addressing the problem of outlier detection, by learning a data-driven scoring function defined on the feature space which reflects the degree of abnormality of the observations. This scoring function is learnt through a well-designed binary classification problem whose empirical criterion takes the form of a two-sample linear rank statistics on which theoretical results are available. We illustrate our methodology with preliminary encouraging numerical experiments.

Affine-Invariant Integrated Rank-Weighted Depth: Definition, Properties and Finite Sample Analysis

Because it determines a center-outward ordering of observations in $\mathbb{R}^d$ with $d\geq 2$, the concept of statistical depth permits to define quantiles and ranks for multivariate data and use them for various statistical tasks (\textit{e.g.} inference, hypothesis testing). Whereas many depth functions have been proposed \textit{ad-hoc} in the literature since the seminal contribution of \cite{Tukey75}, not all of them possess the properties desirable to emulate the notion of quantile function for univariate probability distributions. In this paper, we propose an extension of the \textit{integrated rank-weighted} statistical depth (IRW depth in abbreviated form) originally introduced in \cite{IRW}, modified in order to satisfy the property of \textit{affine-invariance}, fulfilling thus all the four key axioms listed in the nomenclature elaborated by \cite{ZuoS00a}. The variant we propose, referred to as the Affine-Invariant IRW depth (AI-IRW in short), involves the covariance/precision matrices of the (supposedly square integrable) $d$-dimensional random vector $X$ under study, in order to take into account the directions along which $X$ is most variable to assign a depth value to any point $x\in \mathbb{R}^d$. The accuracy of the sampling version of the AI-IRW depth is investigated from a nonasymptotic perspective. Namely, a concentration result for the statistical counterpart of the AI-IRW depth is proved. Beyond the theoretical analysis carried out, applications to anomaly detection are considered and numerical results are displayed, providing strong empirical evidence of the relevance of the depth function we propose here.

Concentration bounds for the empirical angular measure with statistical learning applications

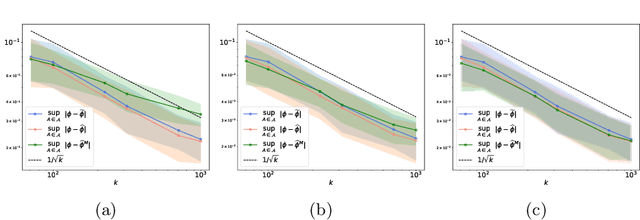
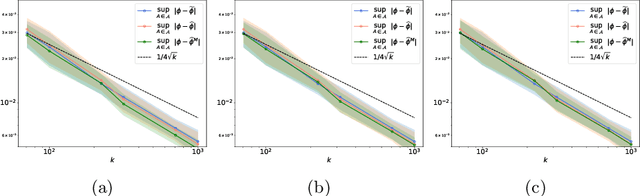
The angular measure on the unit sphere characterizes the first-order dependence structure of the components of a random vector in extreme regions and is defined in terms of standardized margins. Its statistical recovery is an important step in learning problems involving observations far away from the center. In the common situation when the components of the vector have different distributions, the rank transformation offers a convenient and robust way of standardizing data in order to build an empirical version of the angular measure based on the most extreme observations. However, the study of the sampling distribution of the resulting empirical angular measure is challenging. It is the purpose of the paper to establish finite-sample bounds for the maximal deviations between the empirical and true angular measures, uniformly over classes of Borel sets of controlled combinatorial complexity. The bounds are valid with high probability and scale essentially as the square root of the effective sample size, up to a logarithmic factor. Discarding the most extreme observations yields a truncated version of the empirical angular measure for which the logarithmic factor in the concentration bound is replaced by a factor depending on the truncation level. The bounds are applied to provide performance guarantees for two statistical learning procedures tailored to extreme regions of the input space and built upon the empirical angular measure: binary classification in extreme regions through empirical risk minimization and unsupervised anomaly detection through minimum-volume sets of the sphere.

Concentration Inequalities for Two-Sample Rank Processes with Application to Bipartite Ranking

The ROC curve is the gold standard for measuring the performance of a test/scoring statistic regarding its capacity to discriminate between two statistical populations in a wide variety of applications, ranging from anomaly detection in signal processing to information retrieval, through medical diagnosis. Most practical performance measures used in scoring/ranking applications such as the AUC, the local AUC, the p-norm push, the DCG and others, can be viewed as summaries of the ROC curve. In this paper, the fact that most of these empirical criteria can be expressed as two-sample linear rank statistics is highlighted and concentration inequalities for collections of such random variables, referred to as two-sample rank processes here, are proved, when indexed by VC classes of scoring functions. Based on these nonasymptotic bounds, the generalization capacity of empirical maximizers of a wide class of ranking performance criteria is next investigated from a theoretical perspective. It is also supported by empirical evidence through convincing numerical experiments.

Depth-based pseudo-metrics between probability distributions

Data depth is a non parametric statistical tool that measures centrality of any element $x\in\mathbb{R}^d$ with respect to (w.r.t.) a probability distribution or a data set. It is a natural median-oriented extension of the cumulative distribution function (cdf) to the multivariate case. Consequently, its upper level sets -- the depth-trimmed regions -- give rise to a definition of multivariate quantiles. In this work, we propose two new pseudo-metrics between continuous probability measures based on data depth and its associated central regions. The first one is constructed as the Lp-distance between data depth w.r.t. each distribution while the second one relies on the Hausdorff distance between their quantile regions. It can further be seen as an original way to extend the one-dimensional formulae of the Wasserstein distance, which involves quantiles and cdfs, to the multivariate space. After discussing the properties of these pseudo-metrics and providing conditions under which they define a distance, we highlight similarities with the Wasserstein distance. Interestingly, the derived non-asymptotic bounds show that in contrast to the Wasserstein distance, the proposed pseudo-metrics do not suffer from the curse of dimensionality. Moreover, based on the support function of a convex body, we propose an efficient approximation possessing linear time complexity w.r.t. the size of the data set and its dimension. The quality of this approximation as well as the performance of the proposed approach are illustrated in experiments. Furthermore, by construction the regions-based pseudo-metric appears to be robust w.r.t. both outliers and heavy tails, a behavior witnessed in the numerical experiments.