Hamid Jalalzai
Membership Inference Attacks via Adversarial Examples
Jul 27, 2022



Abstract:The raise of machine learning and deep learning led to significant improvement in several domains. This change is supported by both the dramatic rise in computation power and the collection of large datasets. Such massive datasets often include personal data which can represent a threat to privacy. Membership inference attacks are a novel direction of research which aims at recovering training data used by a learning algorithm. In this paper, we develop a mean to measure the leakage of training data leveraging a quantity appearing as a proxy of the total variation of a trained model near its training samples. We extend our work by providing a novel defense mechanism. Our contributions are supported by empirical evidence through convincing numerical experiments.
Leveraging Adversarial Examples to Quantify Membership Information Leakage
Mar 23, 2022



Abstract:The use of personal data for training machine learning systems comes with a privacy threat and measuring the level of privacy of a model is one of the major challenges in machine learning today. Identifying training data based on a trained model is a standard way of measuring the privacy risks induced by the model. We develop a novel approach to address the problem of membership inference in pattern recognition models, relying on information provided by adversarial examples. The strategy we propose consists of measuring the magnitude of a perturbation necessary to build an adversarial example. Indeed, we argue that this quantity reflects the likelihood of belonging to the training data. Extensive numerical experiments on multivariate data and an array of state-of-the-art target models show that our method performs comparable or even outperforms state-of-the-art strategies, but without requiring any additional training samples.
Concentration bounds for the empirical angular measure with statistical learning applications
Apr 07, 2021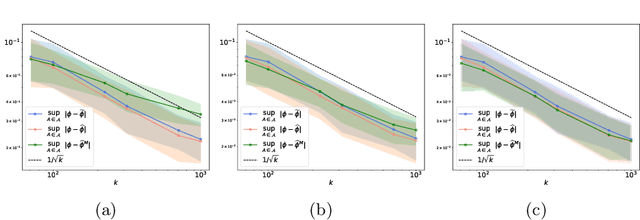
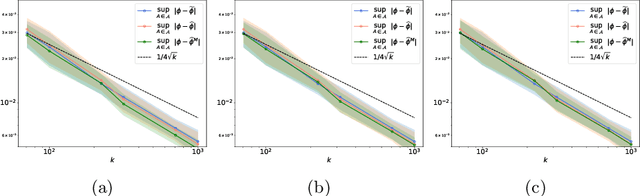
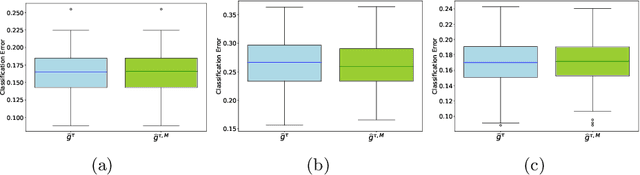
Abstract:The angular measure on the unit sphere characterizes the first-order dependence structure of the components of a random vector in extreme regions and is defined in terms of standardized margins. Its statistical recovery is an important step in learning problems involving observations far away from the center. In the common situation when the components of the vector have different distributions, the rank transformation offers a convenient and robust way of standardizing data in order to build an empirical version of the angular measure based on the most extreme observations. However, the study of the sampling distribution of the resulting empirical angular measure is challenging. It is the purpose of the paper to establish finite-sample bounds for the maximal deviations between the empirical and true angular measures, uniformly over classes of Borel sets of controlled combinatorial complexity. The bounds are valid with high probability and scale essentially as the square root of the effective sample size, up to a logarithmic factor. Discarding the most extreme observations yields a truncated version of the empirical angular measure for which the logarithmic factor in the concentration bound is replaced by a factor depending on the truncation level. The bounds are applied to provide performance guarantees for two statistical learning procedures tailored to extreme regions of the input space and built upon the empirical angular measure: binary classification in extreme regions through empirical risk minimization and unsupervised anomaly detection through minimum-volume sets of the sphere.
Informative Clusters for Multivariate Extremes
Aug 13, 2020



Abstract:Capturing the dependence structure of multivariate extreme data is a major challenge in many fields involving the management of risks that come from multiple sources, e.g., portfolio monitoring, environmental risk management, insurance and anomaly detection. The present paper develops a novel optimization-based approach called MEXICO, standing for Multivariate EXtreme Informative Clustering by Optimization. It aims at exhibiting a sparsity pattern within the dependence structure of extremes. This is achieved by estimating some disjoint clusters of features that tend to be large simultaneously through an optimization method on the probability simplex. This dimension reduction technique can be applied to statistical learning tasks such as feature clustering and anomaly detection. Numerical experiments provide strong empirical evidence of the relevance of our approach.
Heavy-tailed Representations, Text Polarity Classification & Data Augmentation
Mar 25, 2020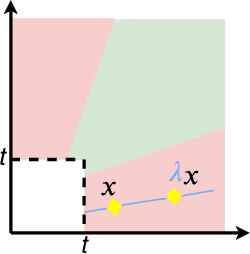
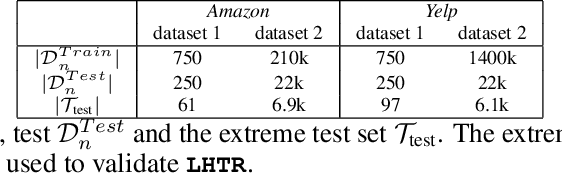
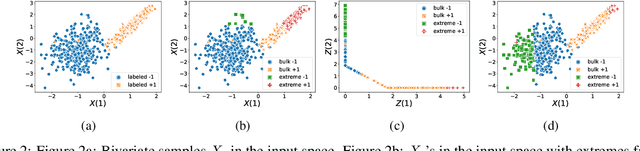
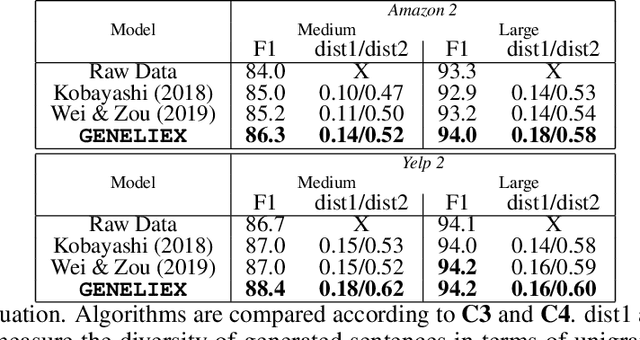
Abstract:The dominant approaches to text representation in natural language rely on learning embeddings on massive corpora which have convenient properties such as compositionality and distance preservation. In this paper, we develop a novel method to learn a heavy-tailed embedding with desirable regularity properties regarding the distributional tails, which allows to analyze the points far away from the distribution bulk using the framework of multivariate extreme value theory. In particular, a classifier dedicated to the tails of the proposed embedding is obtained which performance outperforms the baseline. This classifier exhibits a scale invariance property which we leverage by introducing a novel text generation method for label preserving dataset augmentation. Numerical experiments on synthetic and real text data demonstrate the relevance of the proposed framework and confirm that this method generates meaningful sentences with controllable attribute, e.g. positive or negative sentiment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge