Beyond the Norms: Detecting Prediction Errors in Regression Models

This paper tackles the challenge of detecting unreliable behavior in regression algorithms, which may arise from intrinsic variability (e.g., aleatoric uncertainty) or modeling errors (e.g., model uncertainty). First, we formally introduce the notion of unreliability in regression, i.e., when the output of the regressor exceeds a specified discrepancy (or error). Then, using powerful tools for probabilistic modeling, we estimate the discrepancy density, and we measure its statistical diversity using our proposed metric for statistical dissimilarity. In turn, this allows us to derive a data-driven score that expresses the uncertainty of the regression outcome. We show empirical improvements in error detection for multiple regression tasks, consistently outperforming popular baseline approaches, and contributing to the broader field of uncertainty quantification and safe machine learning systems. Our code is available at https://zenodo.org/records/11281964.

On the feasibility of ML Backdoor Detection as an Hypothesis Testing Problem

We introduce a formal statistical definition for the problem of backdoor detection in machine learning systems and use it to analyze the feasibility of such problems, providing evidence for the utility and applicability of our definition. The main contributions of this work are an impossibility result and an achievability result for backdoor detection. We show a no-free-lunch theorem, proving that universal (adversary-unaware) backdoor detection is impossible, except for very small alphabet sizes. Thus, we argue, that backdoor detection methods need to be either explicitly, or implicitly adversary-aware. However, our work does not imply that backdoor detection cannot work in specific scenarios, as evidenced by successful backdoor detection methods in the scientific literature. Furthermore, we connect our definition to the probably approximately correct (PAC) learnability of the out-of-distribution detection problem.

A Data-Driven Measure of Relative Uncertainty for Misclassification Detection

Misclassification detection is an important problem in machine learning, as it allows for the identification of instances where the model's predictions are unreliable. However, conventional uncertainty measures such as Shannon entropy do not provide an effective way to infer the real uncertainty associated with the model's predictions. In this paper, we introduce a novel data-driven measure of relative uncertainty to an observer for misclassification detection. By learning patterns in the distribution of soft-predictions, our uncertainty measure can identify misclassified samples based on the predicted class probabilities. Interestingly, according to the proposed measure, soft-predictions that correspond to misclassified instances can carry a large amount of uncertainty, even though they may have low Shannon entropy. We demonstrate empirical improvements over multiple image classification tasks, outperforming state-of-the-art misclassification detection methods.

Perfectly Accurate Membership Inference by a Dishonest Central Server in Federated Learning

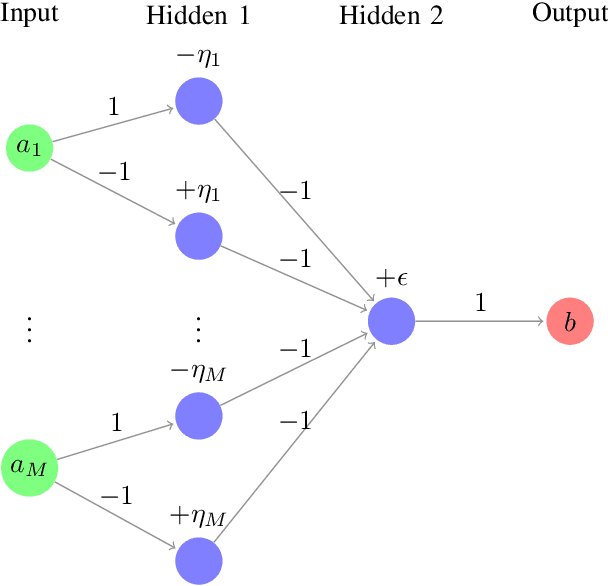
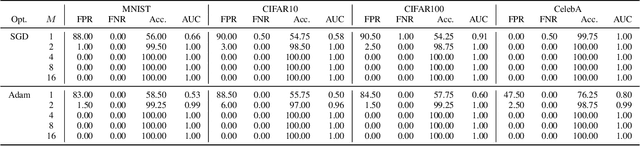
Federated Learning is expected to provide strong privacy guarantees, as only gradients or model parameters but no plain text training data is ever exchanged either between the clients or between the clients and the central server. In this paper, we challenge this claim by introducing a simple but still very effective membership inference attack algorithm, which relies only on a single training step. In contrast to the popular honest-but-curious model, we investigate a framework with a dishonest central server. Our strategy is applicable to models with ReLU activations and uses the properties of this activation function to achieve perfect accuracy. Empirical evaluation on visual classification tasks with MNIST, CIFAR10, CIFAR100 and CelebA datasets show that our method provides perfect accuracy in identifying one sample in a training set with thousands of samples. Occasional failures of our method lead us to discover duplicate images in the CIFAR100 and CelebA datasets.

Leveraging Adversarial Examples to Quantify Membership Information Leakage

The use of personal data for training machine learning systems comes with a privacy threat and measuring the level of privacy of a model is one of the major challenges in machine learning today. Identifying training data based on a trained model is a standard way of measuring the privacy risks induced by the model. We develop a novel approach to address the problem of membership inference in pattern recognition models, relying on information provided by adversarial examples. The strategy we propose consists of measuring the magnitude of a perturbation necessary to build an adversarial example. Indeed, we argue that this quantity reflects the likelihood of belonging to the training data. Extensive numerical experiments on multivariate data and an array of state-of-the-art target models show that our method performs comparable or even outperforms state-of-the-art strategies, but without requiring any additional training samples.

KNIFE: Kernelized-Neural Differential Entropy Estimation

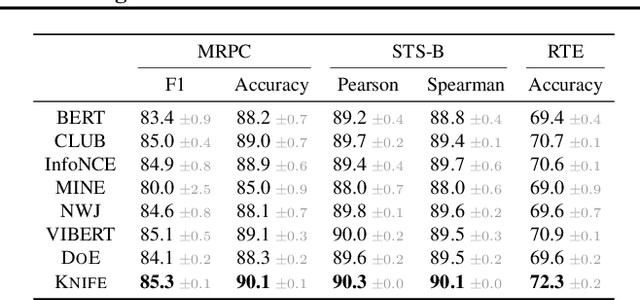
Mutual Information (MI) has been widely used as a loss regularizer for training neural networks. This has been particularly effective when learn disentangled or compressed representations of high dimensional data. However, differential entropy (DE), another fundamental measure of information, has not found widespread use in neural network training. Although DE offers a potentially wider range of applications than MI, off-the-shelf DE estimators are either non differentiable, computationally intractable or fail to adapt to changes in the underlying distribution. These drawbacks prevent them from being used as regularizers in neural networks training. To address shortcomings in previously proposed estimators for DE, here we introduce KNIFE, a fully parameterized, differentiable kernel-based estimator of DE. The flexibility of our approach also allows us to construct KNIFE-based estimators for conditional (on either discrete or continuous variables) DE, as well as MI. We empirically validate our method on high-dimensional synthetic data and further apply it to guide the training of neural networks for real-world tasks. Our experiments on a large variety of tasks, including visual domain adaptation, textual fair classification, and textual fine-tuning demonstrate the effectiveness of KNIFE-based estimation. Code can be found at https://github.com/g-pichler/knife.

Bounding Information Leakage in Machine Learning

Machine Learning services are being deployed in a large range of applications that make it easy for an adversary, using the algorithm and/or the model, to gain access to sensitive data. This paper investigates fundamental bounds on information leakage. First, we identify and bound the success rate of the worst-case membership inference attack, connecting it to the generalization error of the target model. Second, we study the question of how much sensitive information is stored by the algorithm about the training set and we derive bounds on the mutual information between the sensitive attributes and model parameters. Although our contributions are mostly of theoretical nature, the bounds and involved concepts are of practical relevance. Inspired by our theoretical analysis, we study linear regression and DNN models to illustrate how these bounds can be used to assess the privacy guarantees of ML models.

Privacy-Preserving Synthetic Smart Meters Data

Power consumption data is very useful as it allows to optimize power grids, detect anomalies and prevent failures, on top of being useful for diverse research purposes. However, the use of power consumption data raises significant privacy concerns, as this data usually belongs to clients of a power company. As a solution, we propose a method to generate synthetic power consumption samples that faithfully imitate the originals, but are detached from the clients and their identities. Our method is based on Generative Adversarial Networks (GANs). Our contribution is twofold. First, we focus on the quality of the generated data, which is not a trivial task as no standard evaluation methods are available. Then, we study the privacy guarantees provided to members of the training set of our neural network. As a minimum requirement for privacy, we demand our neural network to be robust to membership inference attacks, as these provide a gateway for further attacks in addition to presenting a privacy threat on their own. We find that there is a compromise to be made between the privacy and the performance provided by the algorithm.

On the Estimation of Information Measures of Continuous Distributions

The estimation of information measures of continuous distributions based on samples is a fundamental problem in statistics and machine learning. In this paper, we analyze estimates of differential entropy in $K$-dimensional Euclidean space, computed from a finite number of samples, when the probability density function belongs to a predetermined convex family $\mathcal{P}$. First, estimating differential entropy to any accuracy is shown to be infeasible if the differential entropy of densities in $\mathcal{P}$ is unbounded, clearly showing the necessity of additional assumptions. Subsequently, we investigate sufficient conditions that enable confidence bounds for the estimation of differential entropy. In particular, we provide confidence bounds for simple histogram based estimation of differential entropy from a fixed number of samples, assuming that the probability density function is Lipschitz continuous with known Lipschitz constant and known, bounded support. Our focus is on differential entropy, but we provide examples that show that similar results hold for mutual information and relative entropy as well.

On Direct Distribution Matching for Adapting Segmentation Networks

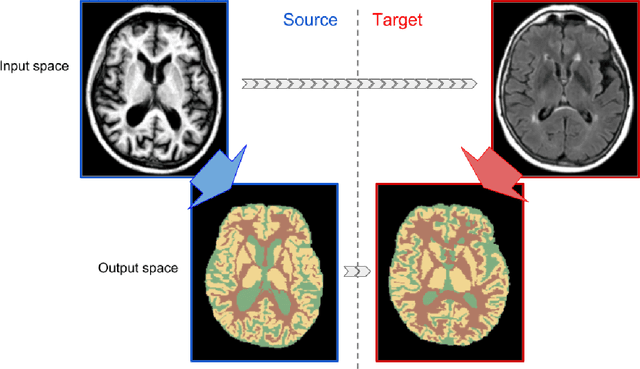
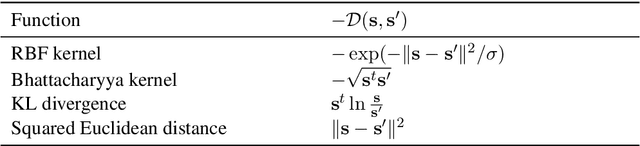
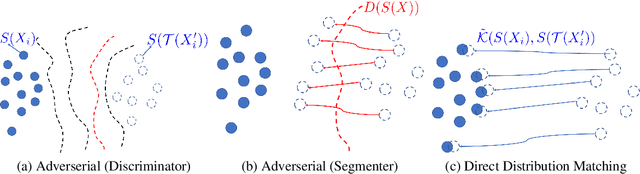
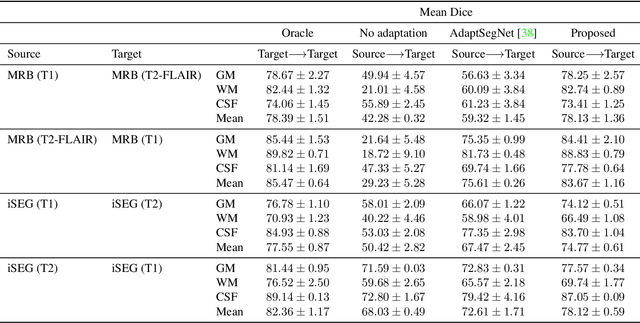
Minimization of distribution matching losses is a principled approach to domain adaptation in the context of image classification. However, it is largely overlooked in adapting segmentation networks, which is currently dominated by adversarial models. We propose a class of loss functions, which encourage direct kernel density matching in the network-output space, up to some geometric transformations computed from unlabeled inputs. Rather than using an intermediate domain discriminator, our direct approach unifies distribution matching and segmentation in a single loss. Therefore, it simplifies segmentation adaptation by avoiding extra adversarial steps, while improving both the quality, stability and efficiency of training. We juxtapose our approach to state-of-the-art segmentation adaptation via adversarial training in the network-output space. In the challenging task of adapting brain segmentation across different magnetic resonance images (MRI) modalities, our approach achieves significantly better results both in terms of accuracy and stability.