Hyperuniformity and non-hyperuniformity of zeros of Gaussian Weyl-Heisenberg Functions

We study zero sets of twisted stationary Gaussian random functions on the complex plane, i.e., Gaussian random functions that are stochastically invariant under the action of the Weyl-Heisenberg group. This model includes translation invariant Gaussian entire functions (GEFs), and also many other non-analytic examples, in which case winding numbers around zeros can be either positive or negative. We investigate zero statistics both when zeros are weighted with their winding numbers (charged zero set) and when they are not (uncharged zero set). We show that the variance of the charged zero statistic always grows linearly with the radius of the observation disk (hyperuniformity). Importantly, this holds for functions with possibly non-zero means and without assuming additional symmetries such as radiality. With respect to uncharged zero statistics, we provide an example for which the variance grows with the area of the observation disk (non-hyperuniformity). This is used to show that, while the zeros of GEFs are hyperuniform, the set of their critical points fails to be so. Our work contributes to recent developments in statistical signal processing, where the time-frequency profile of a non-stationary signal embedded into noise is revealed by performing a statistical test on the zeros of its spectrogram (``silent points''). We show that empirical spectrogram zero counts enjoy moderate deviation from their ensemble averages over large observation windows (something that was previously known only for pure noise). In contrast, we also show that spectogram maxima (``loud points") fail to enjoy a similar property. This gives the first formal evidence for the statistical superiority of silent points over the competing feature of loud points, a fact that has been noted by practitioners.

Grid-Based Decimation for Wavelet Transforms with Stably Invertible Implementation

The constant center frequency to bandwidth ratio (Q-factor) of wavelet transforms provides a very natural representation for audio data. However, invertible wavelet transforms have either required non-uniform decimation -- leading to irregular data structures that are cumbersome to work with -- or require excessively high oversampling with unacceptable computational overhead. Here, we present a novel decimation strategy for wavelet transforms that leads to stable representations with oversampling rates close to one and uniform decimation. Specifically, we show that finite implementations of the resulting representation are energy-preserving in the sense of frame theory. The obtained wavelet coefficients can be stored in a timefrequency matrix with a natural interpretation of columns as time frames and rows as frequency channels. This matrix structure immediately grants access to a large number of algorithms that are successfully used in time-frequency audio processing, but could not previously be used jointly with wavelet transforms. We demonstrate the application of our method in processing based on nonnegative matrix factorization, in onset detection, and in phaseless reconstruction.

Fusion of Probability Density Functions

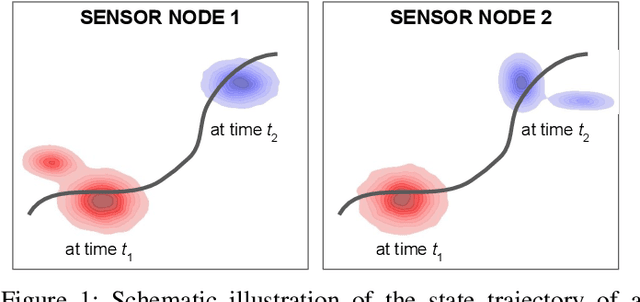
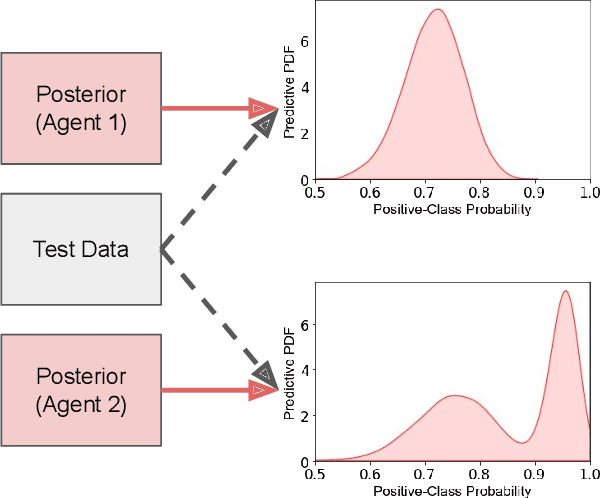
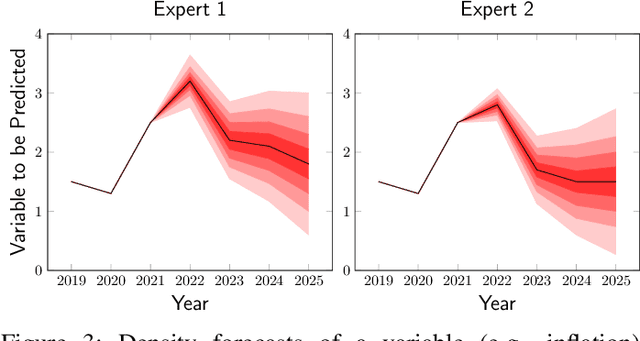
Fusing probabilistic information is a fundamental task in signal and data processing with relevance to many fields of technology and science. In this work, we investigate the fusion of multiple probability density functions (pdfs) of a continuous random variable or vector. Although the case of continuous random variables and the problem of pdf fusion frequently arise in multisensor signal processing, statistical inference, and machine learning, a universally accepted method for pdf fusion does not exist. The diversity of approaches, perspectives, and solutions related to pdf fusion motivates a unified presentation of the theory and methodology of the field. We discuss three different approaches to fusing pdfs. In the axiomatic approach, the fusion rule is defined indirectly by a set of properties (axioms). In the optimization approach, it is the result of minimizing an objective function that involves an information-theoretic divergence or a distance measure. In the supra-Bayesian approach, the fusion center interprets the pdfs to be fused as random observations. Our work is partly a survey, reviewing in a structured and coherent fashion many of the concepts and methods that have been developed in the literature. In addition, we present new results for each of the three approaches. Our original contributions include new fusion rules, axioms, and axiomatic and optimization-based characterizations; a new formulation of supra-Bayesian fusion in terms of finite-dimensional parametrizations; and a study of supra-Bayesian fusion of posterior pdfs for linear Gaussian models.

On the Estimation of Information Measures of Continuous Distributions

The estimation of information measures of continuous distributions based on samples is a fundamental problem in statistics and machine learning. In this paper, we analyze estimates of differential entropy in $K$-dimensional Euclidean space, computed from a finite number of samples, when the probability density function belongs to a predetermined convex family $\mathcal{P}$. First, estimating differential entropy to any accuracy is shown to be infeasible if the differential entropy of densities in $\mathcal{P}$ is unbounded, clearly showing the necessity of additional assumptions. Subsequently, we investigate sufficient conditions that enable confidence bounds for the estimation of differential entropy. In particular, we provide confidence bounds for simple histogram based estimation of differential entropy from a fixed number of samples, assuming that the probability density function is Lipschitz continuous with known Lipschitz constant and known, bounded support. Our focus is on differential entropy, but we provide examples that show that similar results hold for mutual information and relative entropy as well.

Minimal Achievable Sufficient Statistic Learning

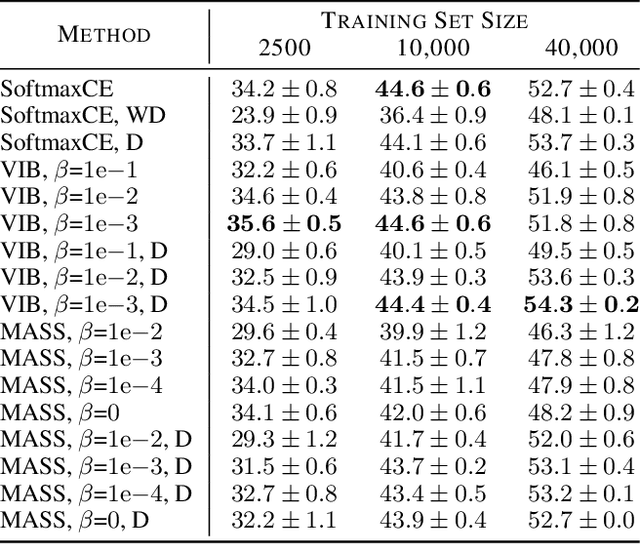
We introduce Minimal Achievable Sufficient Statistic (MASS) Learning, a training method for machine learning models that attempts to produce minimal sufficient statistics with respect to a class of functions (e.g. deep networks) being optimized over. In deriving MASS Learning, we also introduce Conserved Differential Information (CDI), an information-theoretic quantity that - unlike standard mutual information - can be usefully applied to deterministically-dependent continuous random variables like the input and output of a deep network. In a series of experiments, we show that deep networks trained with MASS Learning achieve competitive performance on supervised learning, regularization, and uncertainty quantification benchmarks.