Aliasing in Convnets: A Frame-Theoretic Perspective

Using a stride in a convolutional layer inherently introduces aliasing, which has implications for numerical stability and statistical generalization. While techniques such as the parametrizations via paraunitary systems have been used to promote orthogonal convolution and thus ensure Parseval stability, a general analysis of aliasing and its effects on the stability has not been done in this context. In this article, we adapt a frame-theoretic approach to describe aliasing in convolutional layers with 1D kernels, leading to practical estimates for stability bounds and characterizations of Parseval stability, that are tailored to take short kernel sizes into account. From this, we derive two computationally very efficient optimization objectives that promote Parseval stability via systematically suppressing aliasing. Finally, for layers with random kernels, we derive closed-form expressions for the expected value and variance of the terms that describe the aliasing effects, revealing fundamental insights into the aliasing behavior at initialization.

ISAC: An Invertible and Stable Auditory Filter Bank with Customizable Kernels for ML Integration

This paper introduces ISAC, an invertible and stable, perceptually-motivated filter bank that is specifically designed to be integrated into machine learning paradigms. More precisely, the center frequencies and bandwidths of the filters are chosen to follow a non-linear, auditory frequency scale, the filter kernels have user-defined maximum temporal support and may serve as learnable convolutional kernels, and there exists a corresponding filter bank such that both form a perfect reconstruction pair. ISAC provides a powerful and user-friendly audio front-end suitable for any application, including analysis-synthesis schemes.

Grid-Based Decimation for Wavelet Transforms with Stably Invertible Implementation

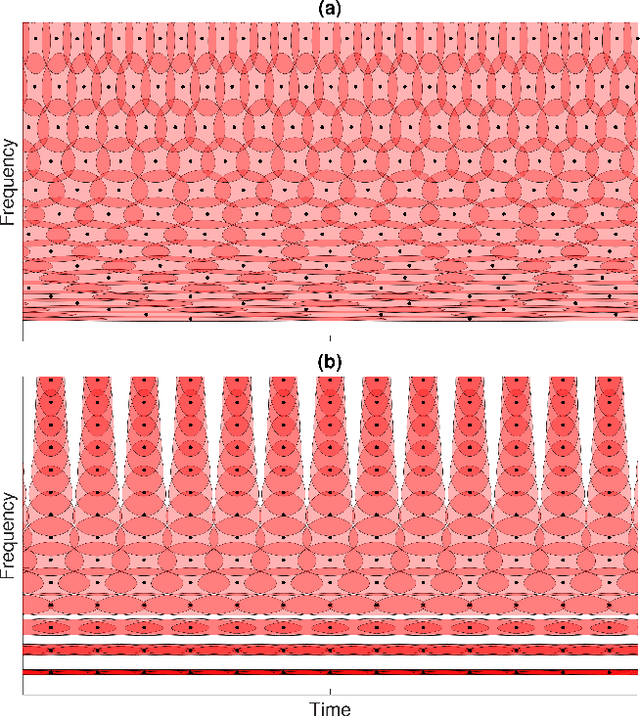
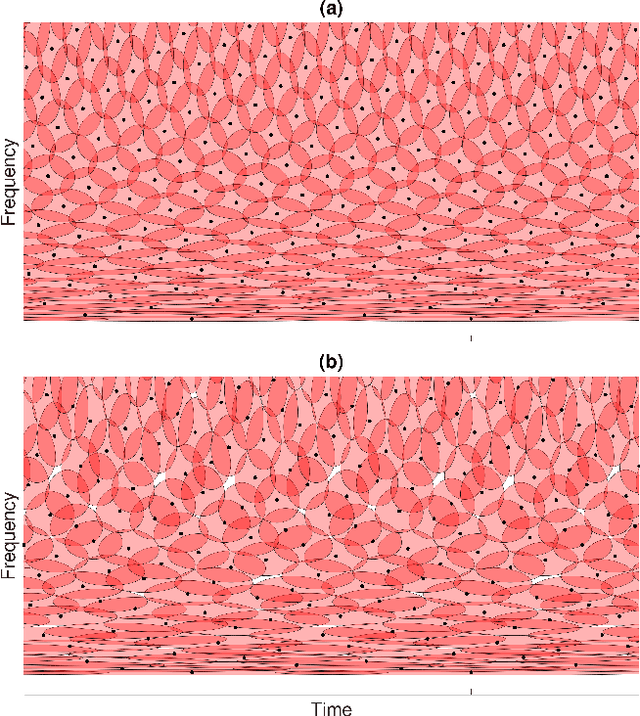
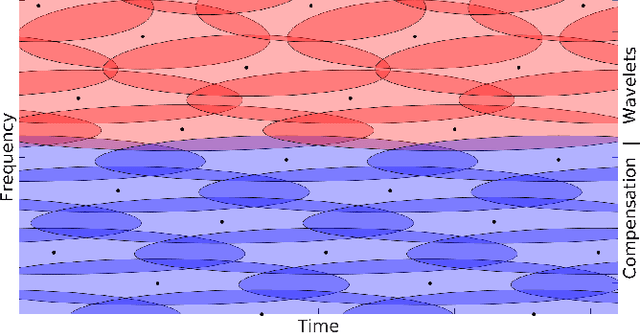
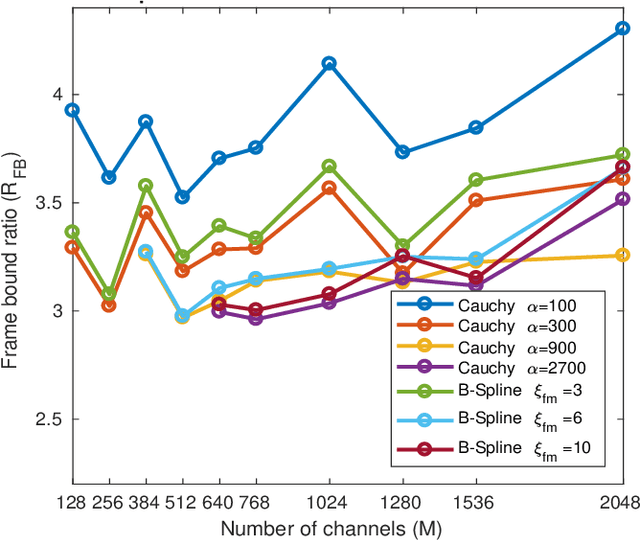
The constant center frequency to bandwidth ratio (Q-factor) of wavelet transforms provides a very natural representation for audio data. However, invertible wavelet transforms have either required non-uniform decimation -- leading to irregular data structures that are cumbersome to work with -- or require excessively high oversampling with unacceptable computational overhead. Here, we present a novel decimation strategy for wavelet transforms that leads to stable representations with oversampling rates close to one and uniform decimation. Specifically, we show that finite implementations of the resulting representation are energy-preserving in the sense of frame theory. The obtained wavelet coefficients can be stored in a timefrequency matrix with a natural interpretation of columns as time frames and rows as frequency channels. This matrix structure immediately grants access to a large number of algorithms that are successfully used in time-frequency audio processing, but could not previously be used jointly with wavelet transforms. We demonstrate the application of our method in processing based on nonnegative matrix factorization, in onset detection, and in phaseless reconstruction.

Fast Matching Pursuit with Multi-Gabor Dictionaries

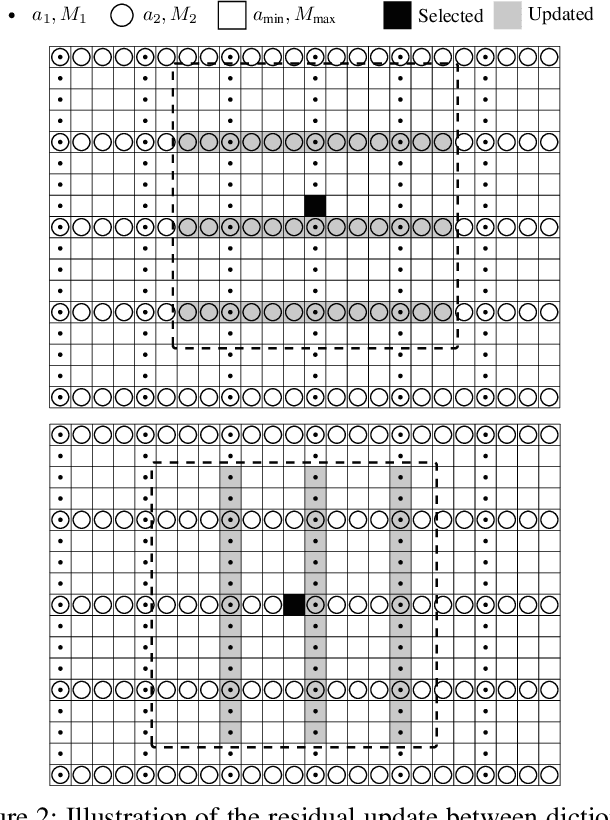
Finding the best K-sparse approximation of a signal in a redundant dictionary is an NP-hard problem. Suboptimal greedy matching pursuit (MP) algorithms are generally used for this task. In this work, we present an acceleration technique and an implementation of the matching pursuit algorithm acting on a multi-Gabor dictionary, i.e., a concatenation of several Gabor-type time-frequency dictionaries, each of which consisting of translations and modulations of a possibly different window and time and frequency shift parameters. The technique is based on pre-computing and thresholding inner products between atoms and on updating the residual directly in the coefficient domain, i.e., without the round-trip to the signal domain. Since the proposed acceleration technique involves an approximate update step, we provide theoretical and experimental results illustrating the convergence of the resulting algorithm. The implementation is written in C (compatible with C99 and C++11) and we also provide Matlab and GNU Octave interfaces. For some settings, the implementation is up to 70 times faster than the standard Matching Pursuit Toolkit (MPTK).

Non-iterative Filter Bank Phase (Re)Construction

Signal reconstruction from magnitude-only measurements presents a long-standing problem in signal processing. In this contribution, we propose a phase (re)construction method for filter banks with uniform decimation and controlled frequency variation. The suggested procedure extends the recently introduced phase-gradient heap integration and relies on a phase-magnitude relationship for filter bank coefficients obtained from Gaussian filters. Admissible filter banks are modeled as the discretization of certain generalized translation-invariant systems, for which we derive the phase-magnitude relationship explicitly. The implementation for discrete signals is described and the performance of the algorithm is evaluated on a range of real and synthetic signals.

Phase-Based Signal Representations for Scattering

The scattering transform is a non-linear signal representation method based on cascaded wavelet transform magnitudes. In this paper we introduce phase scattering, a novel approach where we use phase derivatives in a scattering procedure. We first revisit phase-related concepts for representing time-frequency information of audio signals, in particular, the partial derivatives of the phase in the time-frequency domain. By putting analytical and numerical results in a new light, we set the basis to extend the phase-based representations to higher orders by means of a scattering transform, which leads to well localized signal representations of large-scale structures. All the ideas are introduced in a general way and then applied using the STFT.

Audio Inpainting via $\ell_1$-Minimization and Dictionary Learning

Audio inpainting refers to signal processing techniques that aim at restoring missing or corrupted consecutive samples in audio signals. Prior works have shown that $\ell_1$- minimization with appropriate weighting is capable of solving audio inpainting problems, both for the analysis and the synthesis models. These models assume that audio signals are sparse with respect to some redundant dictionary and exploit that sparsity for inpainting purposes. Remaining within the sparsity framework, we utilize dictionary learning to further increase the sparsity and combine it with weighted $\ell_1$-minimization adapted for audio inpainting to compensate for the loss of energy within the gap after restoration. Our experiments demonstrate that our approach is superior in terms of signal-to-distortion ratio (SDR) and objective difference grade (ODG) compared with its original counterpart.

Phase Vocoder Done Right

The phase vocoder (PV) is a widely spread technique for processing audio signals. It employs a short-time Fourier transform (STFT) analysis-modify-synthesis loop and is typically used for time-scaling of signals by means of using different time steps for STFT analysis and synthesis. The main challenge of PV used for that purpose is the correction of the STFT phase. In this paper, we introduce a novel method for phase correction based on phase gradient estimation and its integration. The method does not require explicit peak picking and tracking nor does it require detection of transients and their separate treatment. Yet, the method does not suffer from the typical phase vocoder artifacts even for extreme time stretching factors.

Time-Frequency Phase Retrieval for Audio -- The Effect of Transform Parameters

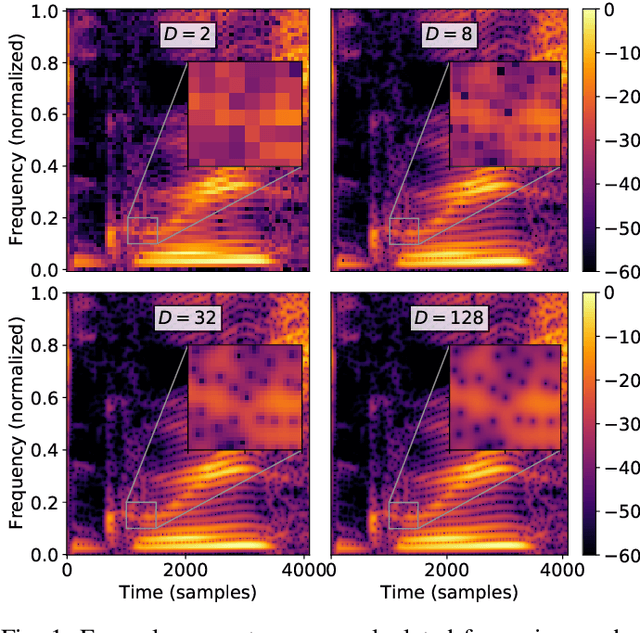
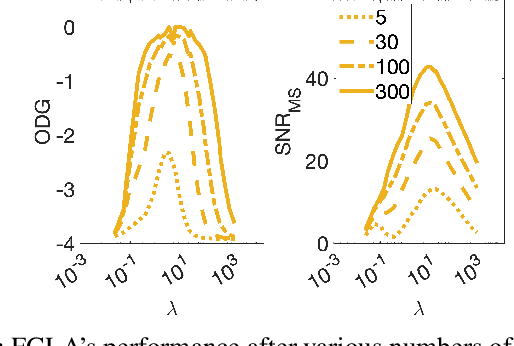
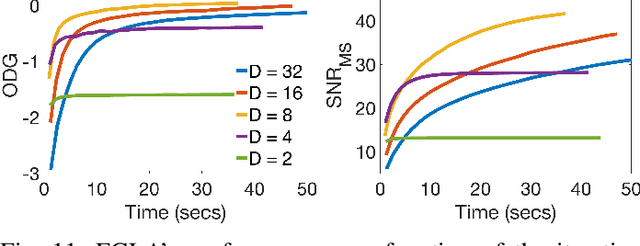
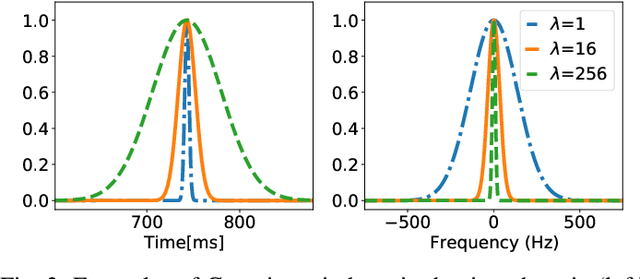
In audio processing applications, phase retrieval (PR) is often performed from the magnitude of short-time Fourier transform (STFT) coefficients. Although PR performance has been observed to depend on the considered STFT parameters and audio data, the extent of this dependence has not been systematically evaluated yet. To address this, we studied the performance of three PR algorithms for various types of audio content and various STFT parameters such as redundancy, time-frequency ratio, and the type of window. The quality of PR was studied in terms of objective difference grade and signal-to-noise ratio of the STFT magnitude, to provide auditory- and signal-based quality assessments. Our results show that PR quality improved with increasing redundancy, with a strong relevance of the time-frequency ratio. The effect of the audio content was smaller but still observable. The effect of the window was only significant for one of the PR algorithms. Interestingly, for a good PR quality, each of the three algorithms required a different set of parameters, demonstrating the relevance of individual parameter sets for a fair comparison across PR algorithms. Based on these results, we developed guidelines for optimizing STFT parameters for a given application.

GACELA -- A generative adversarial context encoder for long audio inpainting

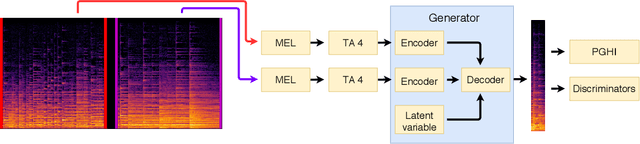
We introduce GACELA, a generative adversarial network (GAN) designed to restore missing musical audio data with a duration ranging between hundreds of milliseconds to a few seconds, i.e., to perform long-gap audio inpainting. While previous work either addressed shorter gaps or relied on exemplars by copying available information from other signal parts, GACELA addresses the inpainting of long gaps in two aspects. First, it considers various time scales of audio information by relying on five parallel discriminators with increasing resolution of receptive fields. Second, it is conditioned not only on the available information surrounding the gap, i.e., the context, but also on the latent variable of the conditional GAN. This addresses the inherent multi-modality of audio inpainting at such long gaps and provides the option of user-defined inpainting. GACELA was tested in listening tests on music signals of varying complexity and gap durations ranging from 375~ms to 1500~ms. While our subjects were often able to detect the inpaintings, the severity of the artifacts decreased from unacceptable to mildly disturbing. GACELA represents a framework capable to integrate future improvements such as processing of more auditory-related features or more explicit musical features.