Hold Me Tight: Stable Encoder-Decoder Design for Speech Enhancement

Convolutional layers with 1-D filters are often used as frontend to encode audio signals. Unlike fixed time-frequency representations, they can adapt to the local characteristics of input data. However, 1-D filters on raw audio are hard to train and often suffer from instabilities. In this paper, we address these problems with hybrid solutions, i.e., combining theory-driven and data-driven approaches. First, we preprocess the audio signals via a auditory filterbank, guaranteeing good frequency localization for the learned encoder. Second, we use results from frame theory to define an unsupervised learning objective that encourages energy conservation and perfect reconstruction. Third, we adapt mixed compressed spectral norms as learning objectives to the encoder coefficients. Using these solutions in a low-complexity encoder-mask-decoder model significantly improves the perceptual evaluation of speech quality (PESQ) in speech enhancement.

Injectivity of ReLU-layers: Perspectives from Frame Theory

Injectivity is the defining property of a mapping that ensures no information is lost and any input can be perfectly reconstructed from its output. By performing hard thresholding, the ReLU function naturally interferes with this property, making the injectivity analysis of ReLU-layers in neural networks a challenging yet intriguing task that has not yet been fully solved. This article establishes a frame theoretic perspective to approach this problem. The main objective is to develop the most general characterization of the injectivity behavior of ReLU-layers in terms of all three involved ingredients: (i) the weights, (ii) the bias, and (iii) the domain where the data is drawn from. Maintaining a focus on practical applications, we limit our attention to bounded domains and present two methods for numerically approximating a maximal bias for given weights and data domains. These methods provide sufficient conditions for the injectivity of a ReLU-layer on those domains and yield a novel practical methodology for studying the information loss in ReLU layers. Finally, we derive explicit reconstruction formulas based on the duality concept from frame theory.

Energy Preservation and Stability of Random Filterbanks

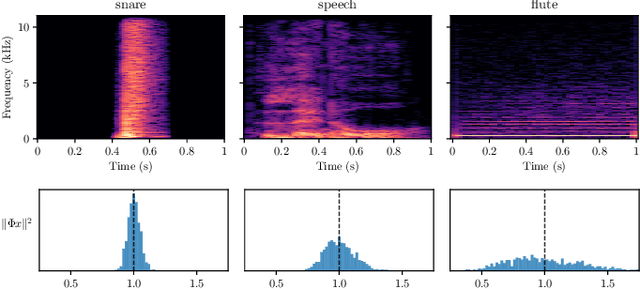
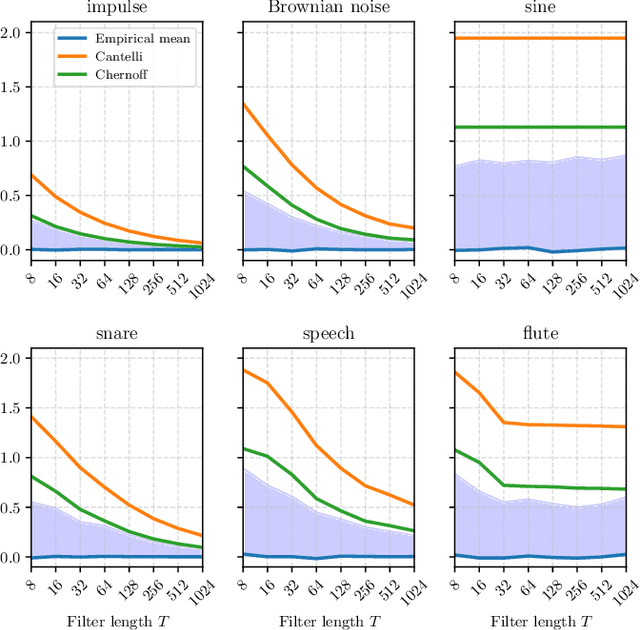
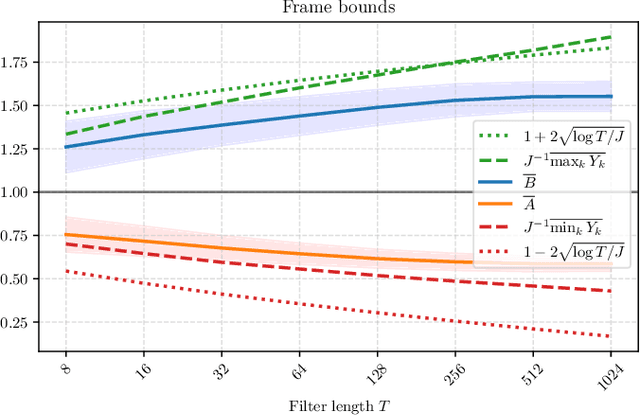
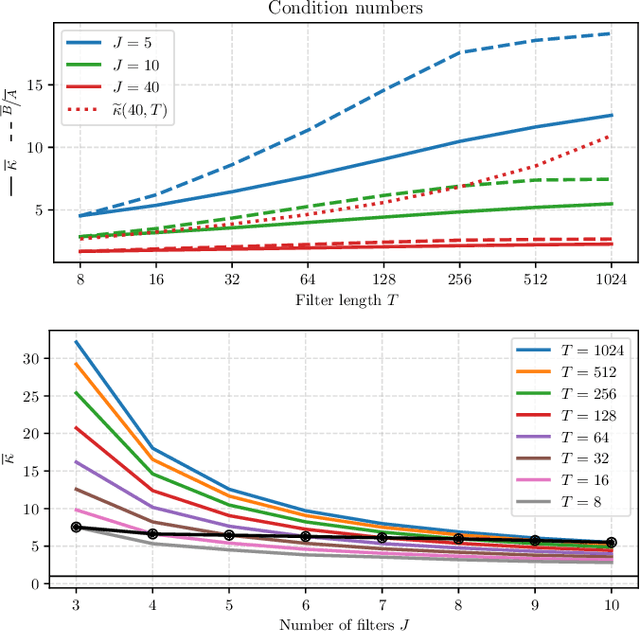
What makes waveform-based deep learning so hard? Despite numerous attempts at training convolutional neural networks (convnets) for filterbank design, they often fail to outperform hand-crafted baselines. This is all the more surprising because these baselines are linear time-invariant systems: as such, their transfer functions could be accurately represented by a convnet with a large receptive field. In this article, we elaborate on the statistical properties of simple convnets from the mathematical perspective of random convolutional operators. We find that FIR filterbanks with random Gaussian weights are ill-conditioned for large filters and locally periodic input signals, which both are typical in audio signal processing applications. Furthermore, we observe that expected energy preservation of a random filterbank is not sufficient for numerical stability and derive theoretical bounds for its expected frame bounds.

Fitting Auditory Filterbanks with Multiresolution Neural Networks

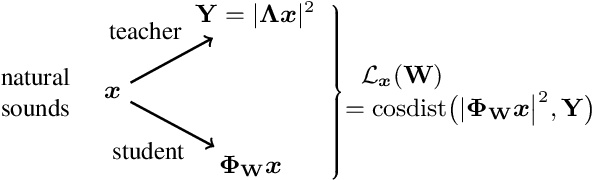
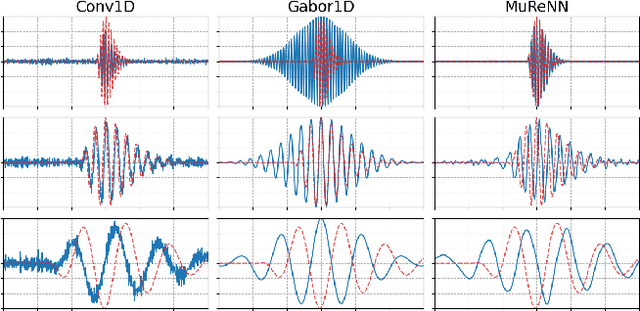
Waveform-based deep learning faces a dilemma between nonparametric and parametric approaches. On one hand, convolutional neural networks (convnets) may approximate any linear time-invariant system; yet, in practice, their frequency responses become more irregular as their receptive fields grow. On the other hand, a parametric model such as LEAF is guaranteed to yield Gabor filters, hence an optimal time-frequency localization; yet, this strong inductive bias comes at the detriment of representational capacity. In this paper, we aim to overcome this dilemma by introducing a neural audio model, named multiresolution neural network (MuReNN). The key idea behind MuReNN is to train separate convolutional operators over the octave subbands of a discrete wavelet transform (DWT). Since the scale of DWT atoms grows exponentially between octaves, the receptive fields of the subsequent learnable convolutions in MuReNN are dilated accordingly. For a given real-world dataset, we fit the magnitude response of MuReNN to that of a well-established auditory filterbank: Gammatone for speech, CQT for music, and third-octave for urban sounds, respectively. This is a form of knowledge distillation (KD), in which the filterbank ''teacher'' is engineered by domain knowledge while the neural network ''student'' is optimized from data. We compare MuReNN to the state of the art in terms of goodness of fit after KD on a hold-out set and in terms of Heisenberg time-frequency localization. Compared to convnets and Gabor convolutions, we find that MuReNN reaches state-of-the-art performance on all three optimization problems.

Convex Geometry of ReLU-layers, Injectivity on the Ball and Local Reconstruction

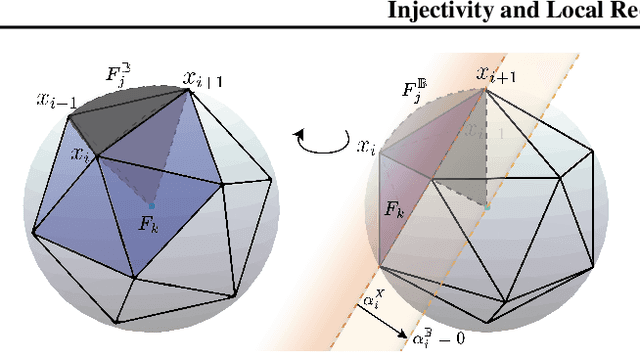
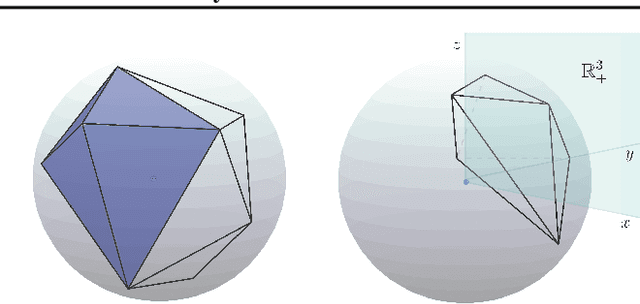
The paper uses a frame-theoretic setting to study the injectivity of a ReLU-layer on the closed ball of $\mathbb{R}^n$ and its non-negative part. In particular, the interplay between the radius of the ball and the bias vector is emphasized. Together with a perspective from convex geometry, this leads to a computationally feasible method of verifying the injectivity of a ReLU-layer under reasonable restrictions in terms of an upper bound of the bias vector. Explicit reconstruction formulas are provided, inspired by the duality concept from frame theory. All this gives rise to the possibility of quantifying the invertibility of a ReLU-layer and a concrete reconstruction algorithm for any input vector on the ball.

visClust: A visual clustering algorithm based on orthogonal projections

We present a novel clustering algorithm, visClust, that is based on lower dimensional data representations and visual interpretation. Thereto, we design a transformation that allows the data to be represented by a binary integer array enabling the further use of image processing methods to select a partition. Qualitative and quantitative analyses show that the algorithm obtains high accuracy (measured with an adjusted one-sided Rand-Index) and requires low runtime and RAM. We compare the results to 6 state-of-the-art algorithms, confirming the quality of visClust by outperforming in most experiments. Moreover, the algorithm asks for just one obligatory input parameter while allowing optimization via optional parameters. The code is made available on GitHub.

Blood vessel segmentation in en-face OCTA images: a frequency based method

Optical coherence tomography angiography (OCTA) is a novel noninvasive imaging modality for visualization of retinal blood flow in the human retina. Using specific OCTA imaging biomarkers for the identification of pathologies, automated image segmentations of the blood vessels can improve subsequent analysis and diagnosis. We present a novel method for the vessel identification based on frequency representations of the image, in particular, using so-called Gabor filter banks. The algorithm is evaluated on an OCTA image data set from $10$ eyes acquired by a Cirrus HD-OCT device. The segmentation outcomes received very good qualitative visual evaluation feedback and coincide well with device-specific values concerning vessel density. Concerning locality our segmentations are even more reliable and accurate. Therefore, we suggest the computation of adaptive local vessel density maps that allow straightforward analysis of retinal blood flow.

An amplified-target loss approach for photoreceptor layer segmentation in pathological OCT scans

Segmenting anatomical structures such as the photoreceptor layer in retinal optical coherence tomography (OCT) scans is challenging in pathological scenarios. Supervised deep learning models trained with standard loss functions are usually able to characterize only the most common disease appeareance from a training set, resulting in suboptimal performance and poor generalization when dealing with unseen lesions. In this paper we propose to overcome this limitation by means of an augmented target loss function framework. We introduce a novel amplified-target loss that explicitly penalizes errors within the central area of the input images, based on the observation that most of the challenging disease appeareance is usually located in this area. We experimentally validated our approach using a data set with OCT scans of patients with macular diseases. We observe increased performance compared to the models that use only the standard losses. Our proposed loss function strongly supports the segmentation model to better distinguish photoreceptors in highly pathological scenarios.

On orthogonal projections for dimension reduction and applications in variational loss functions for learning problems

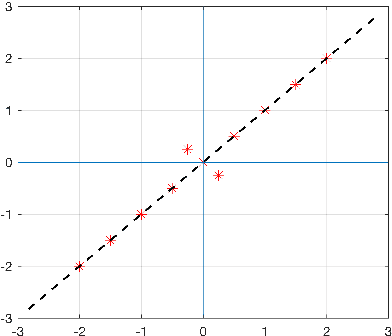
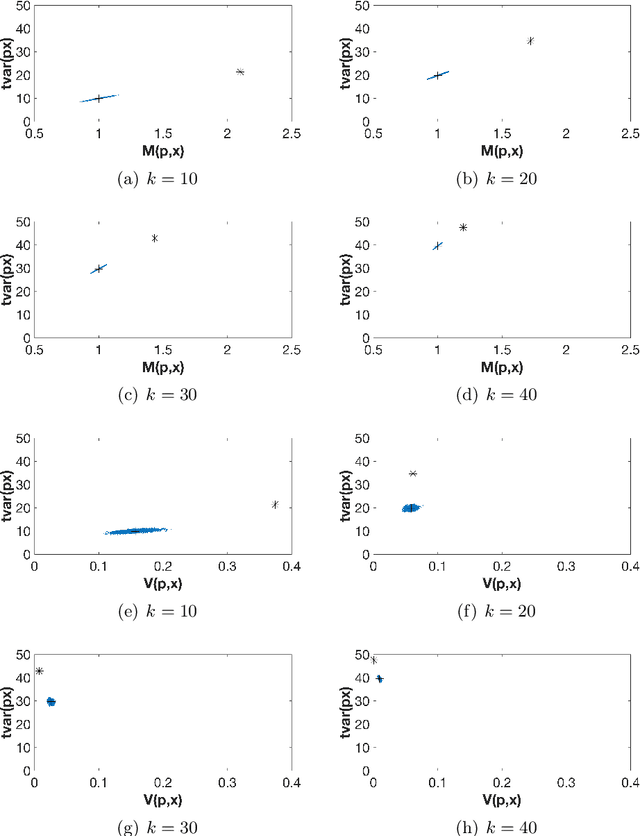
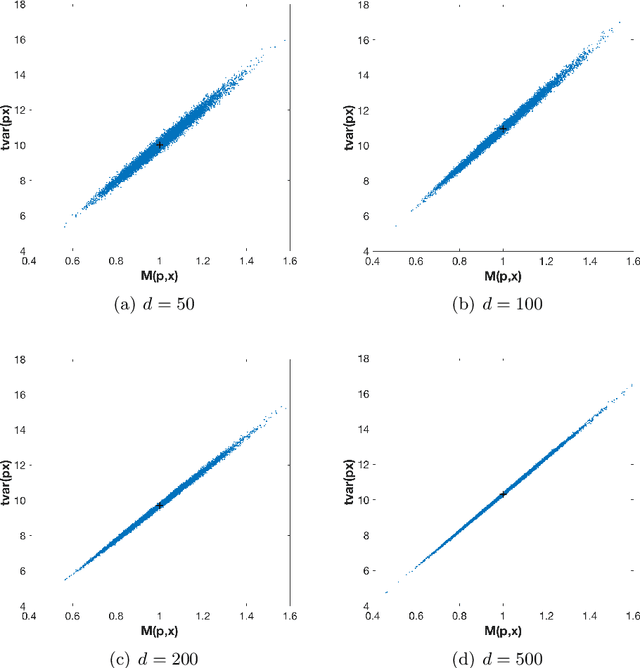
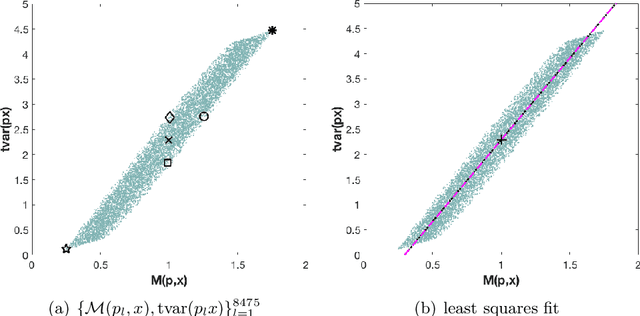
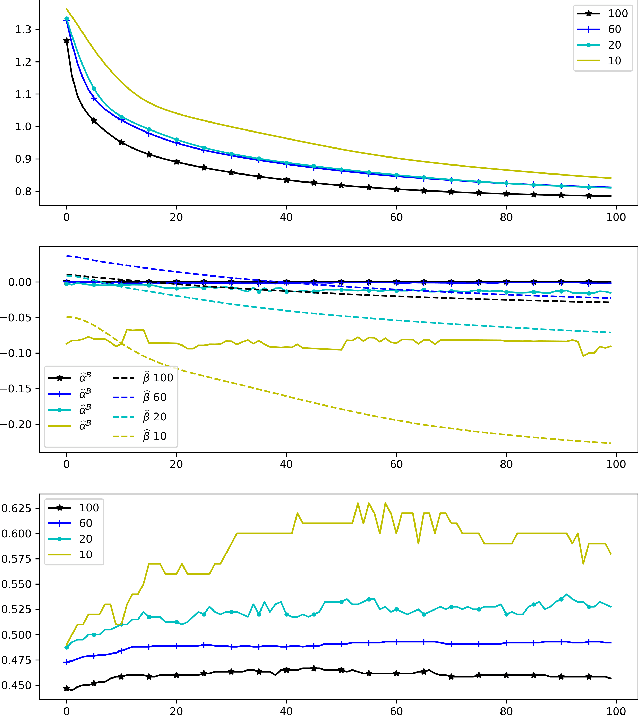
The use of orthogonal projections on high-dimensional input and target data in learning frameworks is studied. First, we investigate the relations between two standard objectives in dimension reduction, maximizing variance and preservation of pairwise relative distances. The derivation of their asymptotic correlation and numerical experiments tell that a projection usually cannot satisfy both objectives. In a standard classification problem we determine projections on the input data that balance them and compare subsequent results. Next, we extend our application of orthogonal projections to deep learning frameworks. We introduce new variational loss functions that enable integration of additional information via transformations and projections of the target data. In two supervised learning problems, clinical image segmentation and music information classification, the application of the proposed loss functions increase the accuracy.

The Algebraic Approach to Phase Retrieval and Explicit Inversion at the Identifiability Threshold

We study phase retrieval from magnitude measurements of an unknown signal as an algebraic estimation problem. Indeed, phase retrieval from rank-one and more general linear measurements can be treated in an algebraic way. It is verified that a certain number of generic rank-one or generic linear measurements are sufficient to enable signal reconstruction for generic signals, and slightly more generic measurements yield reconstructability for all signals. Our results solve a few open problems stated in the recent literature. Furthermore, we show how the algebraic estimation problem can be solved by a closed-form algebraic estimation technique, termed ideal regression, providing non-asymptotic success guarantees.