AGE Challenge: Angle Closure Glaucoma Evaluation in Anterior Segment Optical Coherence Tomography

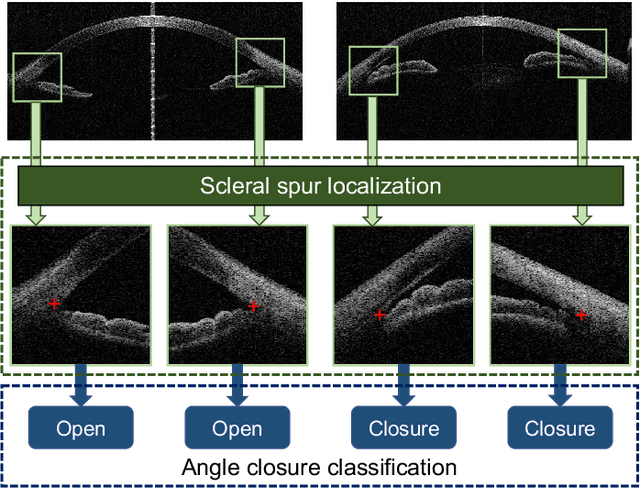
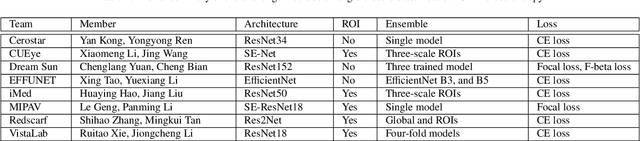
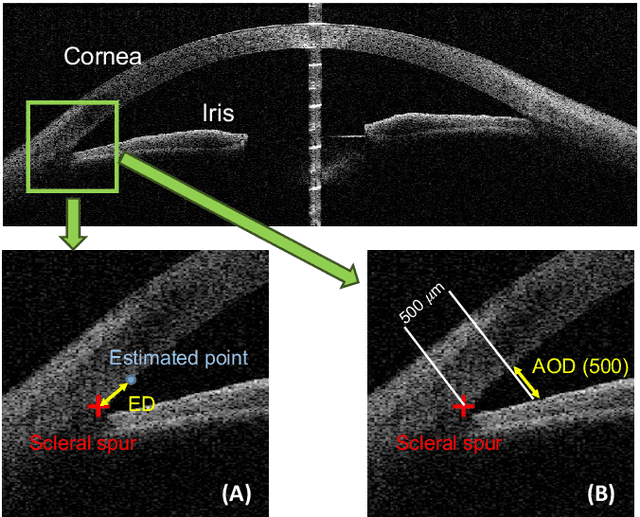
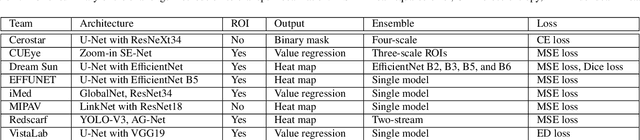
Angle closure glaucoma (ACG) is a more aggressive disease than open-angle glaucoma, where the abnormal anatomical structures of the anterior chamber angle (ACA) may cause an elevated intraocular pressure and gradually leads to glaucomatous optic neuropathy and eventually to visual impairment and blindness. Anterior Segment Optical Coherence Tomography (AS-OCT) imaging provides a fast and contactless way to discriminate angle closure from open angle. Although many medical image analysis algorithms have been developed for glaucoma diagnosis, only a few studies have focused on AS-OCT imaging. In particular, there is no public AS-OCT dataset available for evaluating the existing methods in a uniform way, which limits the progress in the development of automated techniques for angle closure detection and assessment. To address this, we organized the Angle closure Glaucoma Evaluation challenge (AGE), held in conjunction with MICCAI 2019. The AGE challenge consisted of two tasks: scleral spur localization and angle closure classification. For this challenge, we released a large data of 4800 annotated AS-OCT images from 199 patients, and also proposed an evaluation framework to benchmark and compare different models. During the AGE challenge, over 200 teams registered online, and more than 1100 results were submitted for online evaluation. Finally, eight teams participated in the onsite challenge. In this paper, we summarize these eight onsite challenge methods and analyze their corresponding results in the two tasks. We further discuss limitations and future directions. In the AGE challenge, the top-performing approach had an average Euclidean Distance of 10 pixel in scleral spur localization, while in the task of angle closure classification, all the algorithms achieved the satisfactory performances, especially, 100% accuracy rate for top-two performances.

On orthogonal projections for dimension reduction and applications in variational loss functions for learning problems

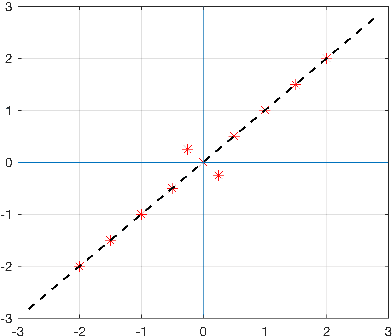
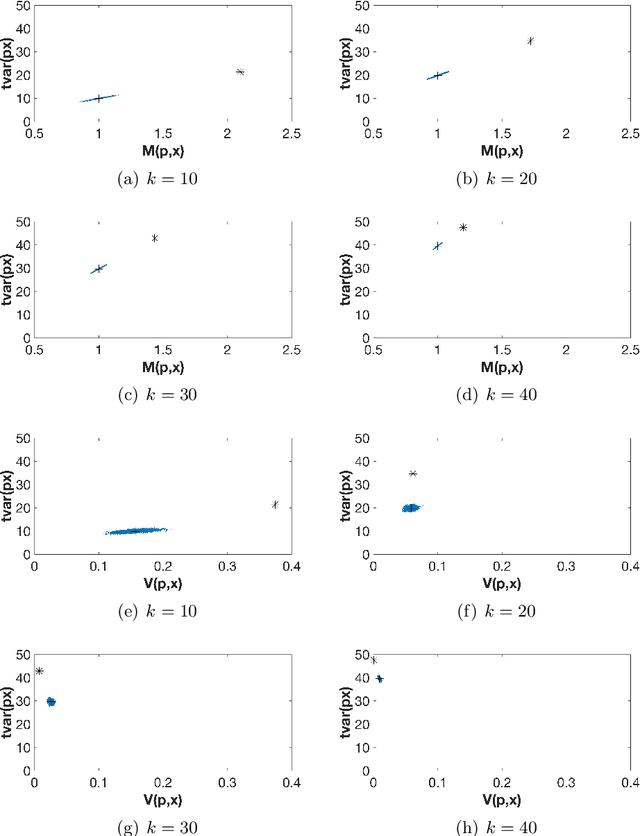
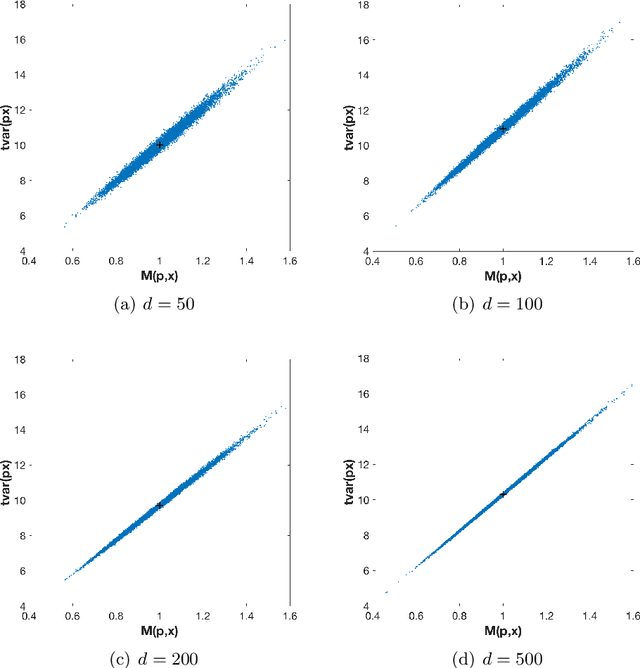
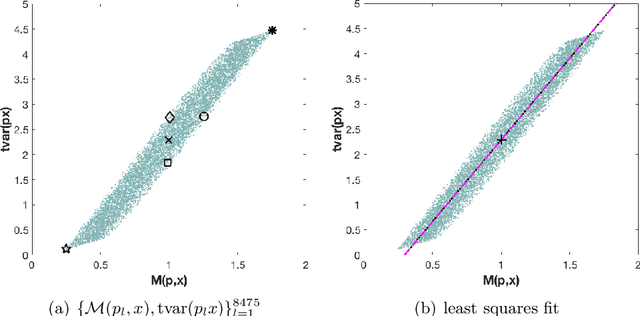
The use of orthogonal projections on high-dimensional input and target data in learning frameworks is studied. First, we investigate the relations between two standard objectives in dimension reduction, maximizing variance and preservation of pairwise relative distances. The derivation of their asymptotic correlation and numerical experiments tell that a projection usually cannot satisfy both objectives. In a standard classification problem we determine projections on the input data that balance them and compare subsequent results. Next, we extend our application of orthogonal projections to deep learning frameworks. We introduce new variational loss functions that enable integration of additional information via transformations and projections of the target data. In two supervised learning problems, clinical image segmentation and music information classification, the application of the proposed loss functions increase the accuracy.