Redistributor: Transforming Empirical Data Distributions

We present an algorithm and package, Redistributor, which forces a collection of scalar samples to follow a desired distribution. When given independent and identically distributed samples of some random variable $S$ and the continuous cumulative distribution function of some desired target $T$, it provably produces a consistent estimator of the transformation $R$ which satisfies $R(S)=T$ in distribution. As the distribution of $S$ or $T$ may be unknown, we also include algorithms for efficiently estimating these distributions from samples. This allows for various interesting use cases in image processing, where Redistributor serves as a remarkably simple and easy-to-use tool that is capable of producing visually appealing results. The package is implemented in Python and is optimized to efficiently handle large data sets, making it also suitable as a preprocessing step in machine learning. The source code is available at https://gitlab.com/paloha/redistributor.

Learning Complex Basis Functions for Invariant Representations of Audio

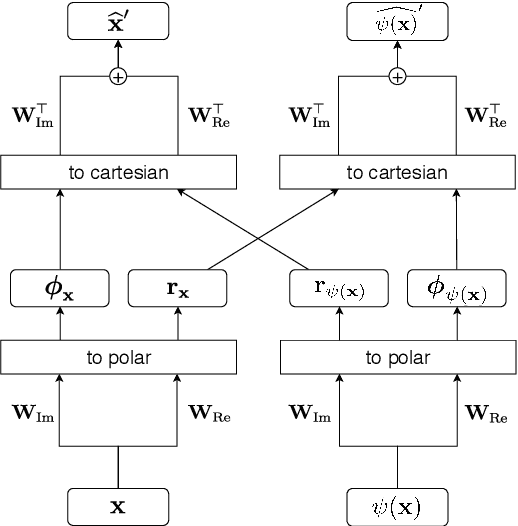
Learning features from data has shown to be more successful than using hand-crafted features for many machine learning tasks. In music information retrieval (MIR), features learned from windowed spectrograms are highly variant to transformations like transposition or time-shift. Such variances are undesirable when they are irrelevant for the respective MIR task. We propose an architecture called Complex Autoencoder (CAE) which learns features invariant to orthogonal transformations. Mapping signals onto complex basis functions learned by the CAE results in a transformation-invariant "magnitude space" and a transformation-variant "phase space". The phase space is useful to infer transformations between data pairs. When exploiting the invariance-property of the magnitude space, we achieve state-of-the-art results in audio-to-score alignment and repeated section discovery for audio. A PyTorch implementation of the CAE, including the repeated section discovery method, is available online.

Machines listening to music: the role of signal representations in learning from music

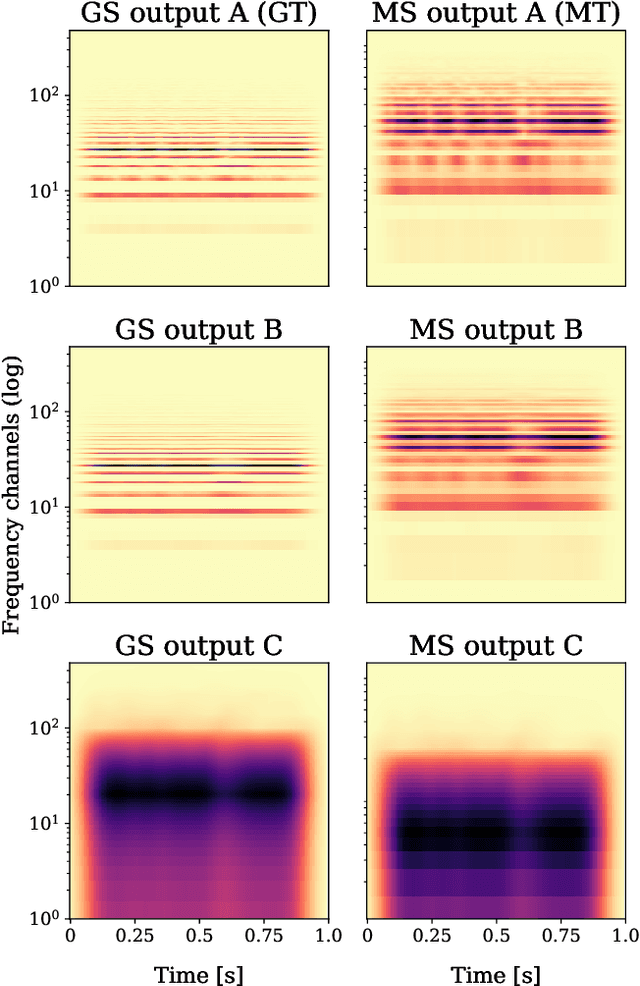
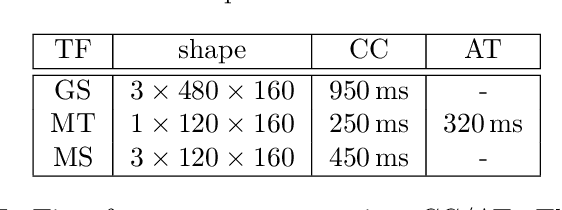
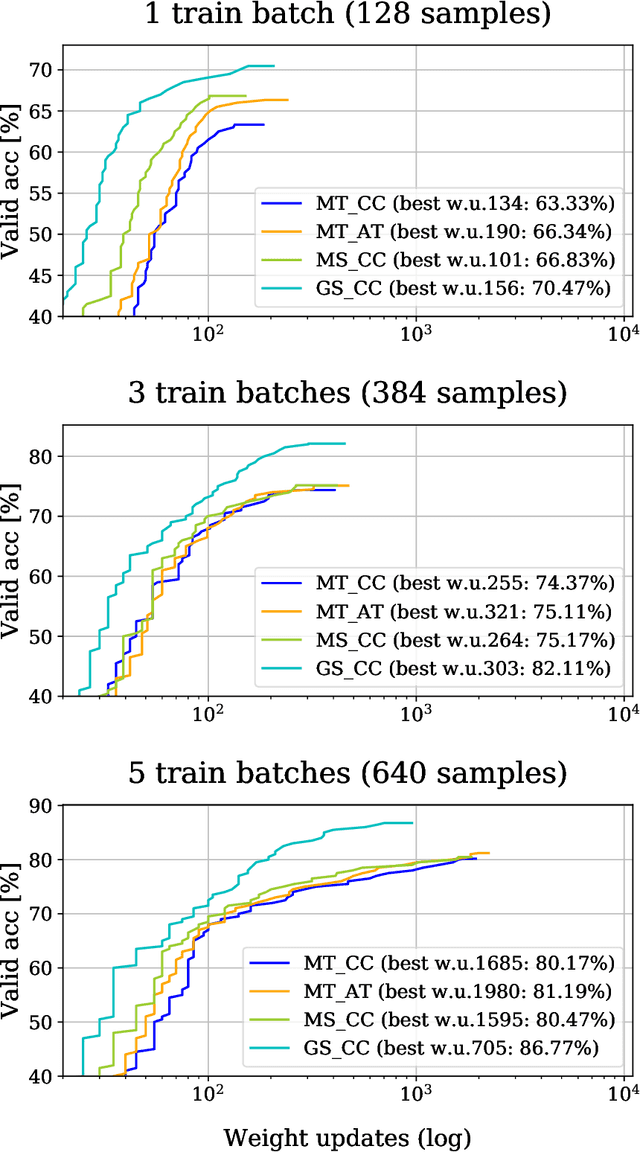
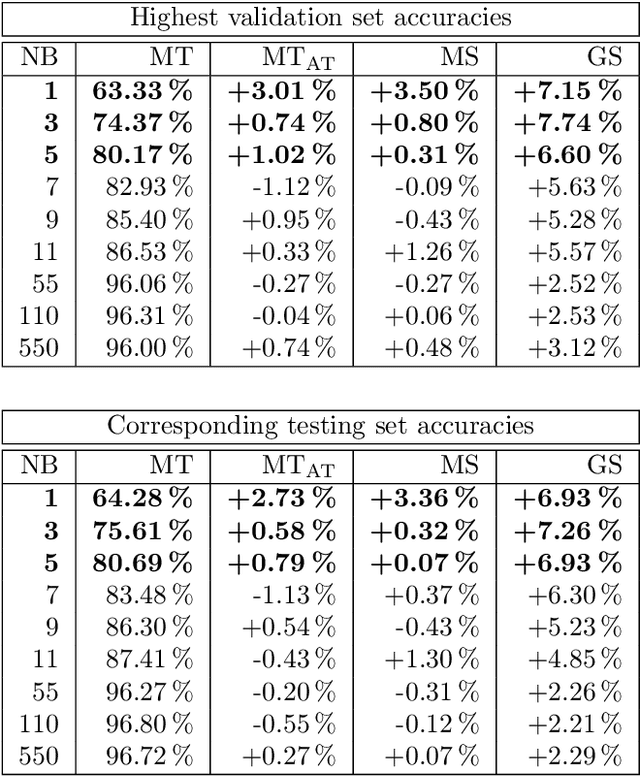
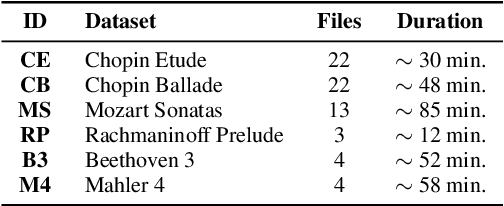
Recent, extremely successful methods in deep learning, such as convolutional neural networks (CNNs) have originated in machine learning for images. When applied to music signals and related music information retrieval (MIR) problems, researchers often apply standard FFT-based signal processing methods in order to create an image from the raw audio data. The impact of this basic signal processing step on the final outcome of the MIR task has not been widely studied and is not well understood. In this contribution, we study Gabor Scattering and a new representation, namely Mel Scattering. Furthermore, we suggest an alternative enhancement of the loss function that uses transformed representations of the output data to incorporate additional available information. We show how applying various different signal analysis methods can lead to useful invariances and improve the overall performance in MIR problems by reducing the amount of necessary training data or the necessity of augmentation.

On orthogonal projections for dimension reduction and applications in variational loss functions for learning problems

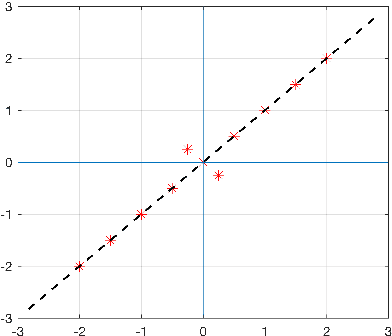
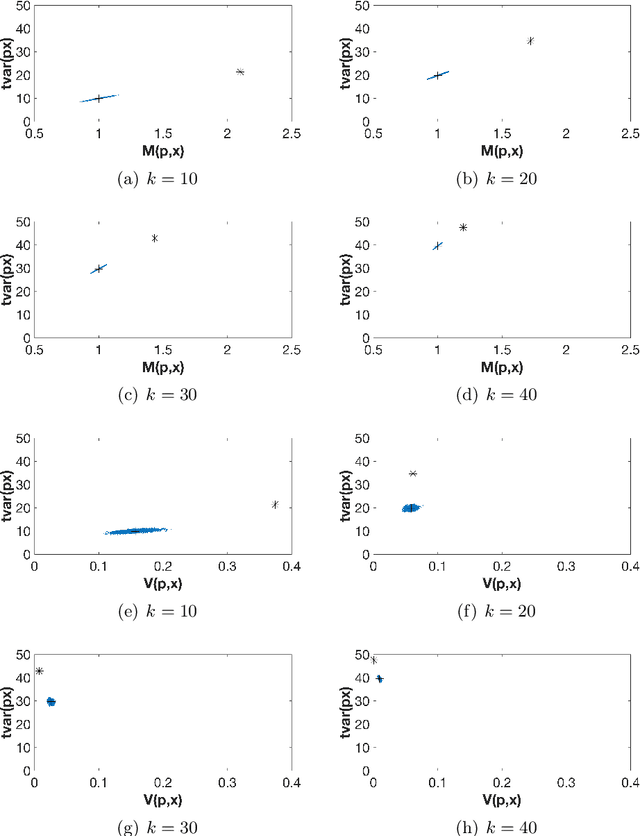
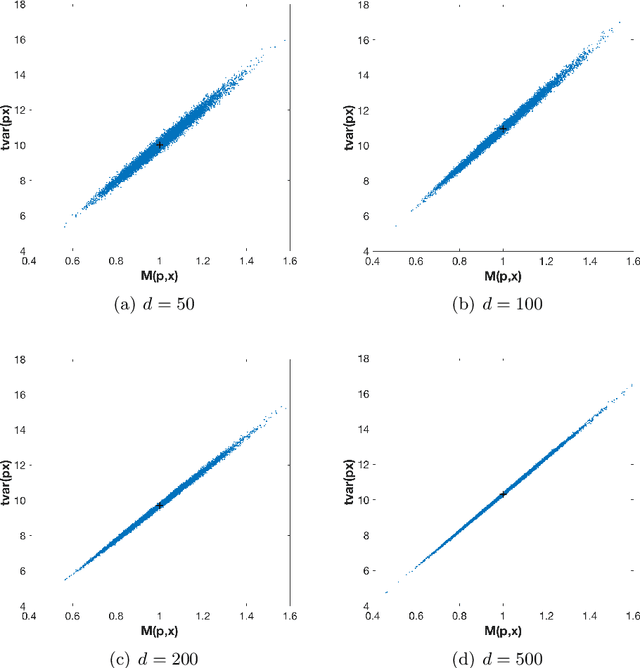
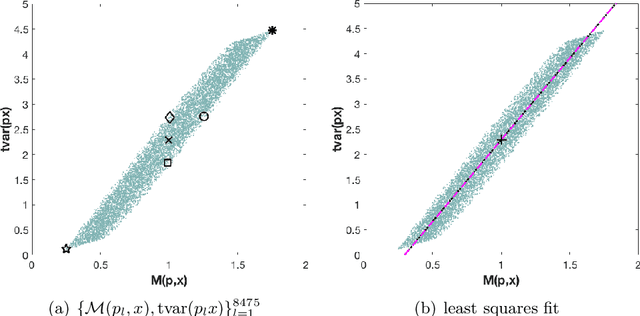
The use of orthogonal projections on high-dimensional input and target data in learning frameworks is studied. First, we investigate the relations between two standard objectives in dimension reduction, maximizing variance and preservation of pairwise relative distances. The derivation of their asymptotic correlation and numerical experiments tell that a projection usually cannot satisfy both objectives. In a standard classification problem we determine projections on the input data that balance them and compare subsequent results. Next, we extend our application of orthogonal projections to deep learning frameworks. We introduce new variational loss functions that enable integration of additional information via transformations and projections of the target data. In two supervised learning problems, clinical image segmentation and music information classification, the application of the proposed loss functions increase the accuracy.

Gabor frames and deep scattering networks in audio processing

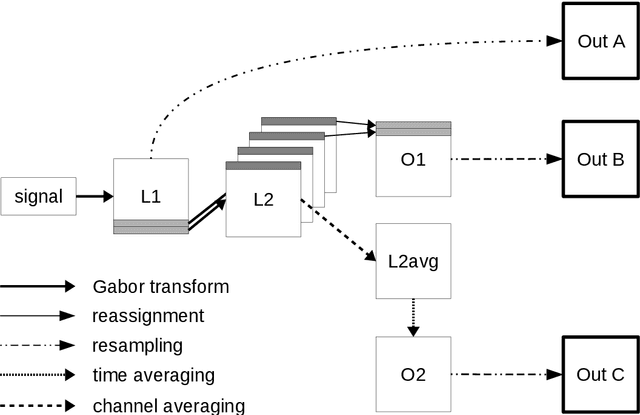
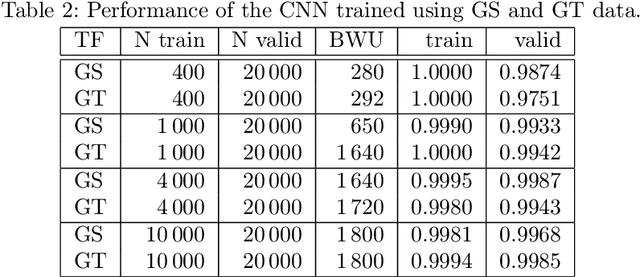
In this paper a feature extractor based on Gabor frames and Mallat's scattering transform, called Gabor scattering, is introduced. This feature extractor is applied to a simple signal model for audio signals, i.e. a class of tones consisting of fundamental frequency and its multiples and an according envelope. Within different layers, different invariances to certain signal features occur. In this paper we give a mathematical explanation for the first and the second layer which are illustrated by numerical examples. Deformation stability of this feature extractor will be shown by using a decoupling technique, previously suggested for the scattering transform of Cartoon functions. Here it is used to see if the feature extractor is robust to changes in spectral shape and frequency modulation.