ISAC: An Invertible and Stable Auditory Filter Bank with Customizable Kernels for ML Integration

This paper introduces ISAC, an invertible and stable, perceptually-motivated filter bank that is specifically designed to be integrated into machine learning paradigms. More precisely, the center frequencies and bandwidths of the filters are chosen to follow a non-linear, auditory frequency scale, the filter kernels have user-defined maximum temporal support and may serve as learnable convolutional kernels, and there exists a corresponding filter bank such that both form a perfect reconstruction pair. ISAC provides a powerful and user-friendly audio front-end suitable for any application, including analysis-synthesis schemes.

Construction of generalized samplets in Banach spaces

Recently, samplets have been introduced as localized discrete signed measures which are tailored to an underlying data set. Samplets exhibit vanishing moments, i.e., their measure integrals vanish for all polynomials up to a certain degree, which allows for feature detection and data compression. In the present article, we extend the different construction steps of samplets to functionals in Banach spaces more general than point evaluations. To obtain stable representations, we assume that these functionals form frames with square-summable coefficients or even Riesz bases with square-summable coefficients. In either case, the corresponding analysis operator is injective and we obtain samplet bases with the desired properties by means of constructing an isometry of the analysis operator's image. Making the assumption that the dual of the Banach space under consideration is imbedded into the space of compactly supported distributions, the multilevel hierarchy for the generalized samplet construction is obtained by spectral clustering of a similarity graph for the functionals' supports. Based on this multilevel hierarchy, generalized samplets exhibit vanishing moments with respect to a given set of primitives within the Banach space. We derive an abstract localization result for the generalized samplet coefficients with respect to the samplets' support sizes and the approximability of the Banach space elements by the chosen primitives. Finally, we present three examples showcasing the generalized samplet framework.

Hold Me Tight: Stable Encoder-Decoder Design for Speech Enhancement

Convolutional layers with 1-D filters are often used as frontend to encode audio signals. Unlike fixed time-frequency representations, they can adapt to the local characteristics of input data. However, 1-D filters on raw audio are hard to train and often suffer from instabilities. In this paper, we address these problems with hybrid solutions, i.e., combining theory-driven and data-driven approaches. First, we preprocess the audio signals via a auditory filterbank, guaranteeing good frequency localization for the learned encoder. Second, we use results from frame theory to define an unsupervised learning objective that encourages energy conservation and perfect reconstruction. Third, we adapt mixed compressed spectral norms as learning objectives to the encoder coefficients. Using these solutions in a low-complexity encoder-mask-decoder model significantly improves the perceptual evaluation of speech quality (PESQ) in speech enhancement.

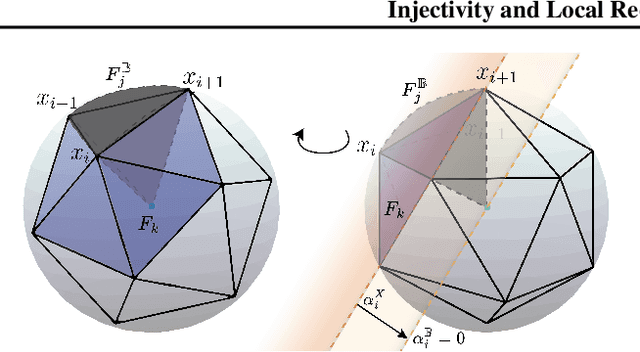
Injectivity of ReLU-layers: Perspectives from Frame Theory

Injectivity is the defining property of a mapping that ensures no information is lost and any input can be perfectly reconstructed from its output. By performing hard thresholding, the ReLU function naturally interferes with this property, making the injectivity analysis of ReLU-layers in neural networks a challenging yet intriguing task that has not yet been fully solved. This article establishes a frame theoretic perspective to approach this problem. The main objective is to develop the most general characterization of the injectivity behavior of ReLU-layers in terms of all three involved ingredients: (i) the weights, (ii) the bias, and (iii) the domain where the data is drawn from. Maintaining a focus on practical applications, we limit our attention to bounded domains and present two methods for numerically approximating a maximal bias for given weights and data domains. These methods provide sufficient conditions for the injectivity of a ReLU-layer on those domains and yield a novel practical methodology for studying the information loss in ReLU layers. Finally, we derive explicit reconstruction formulas based on the duality concept from frame theory.

Energy Preservation and Stability of Random Filterbanks

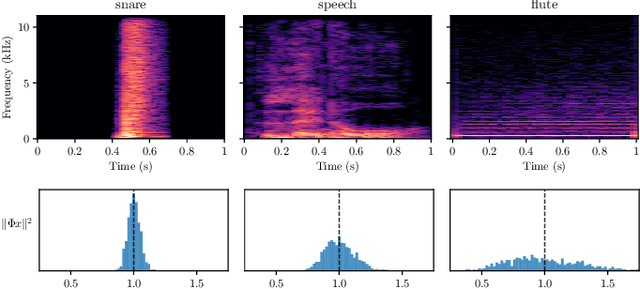
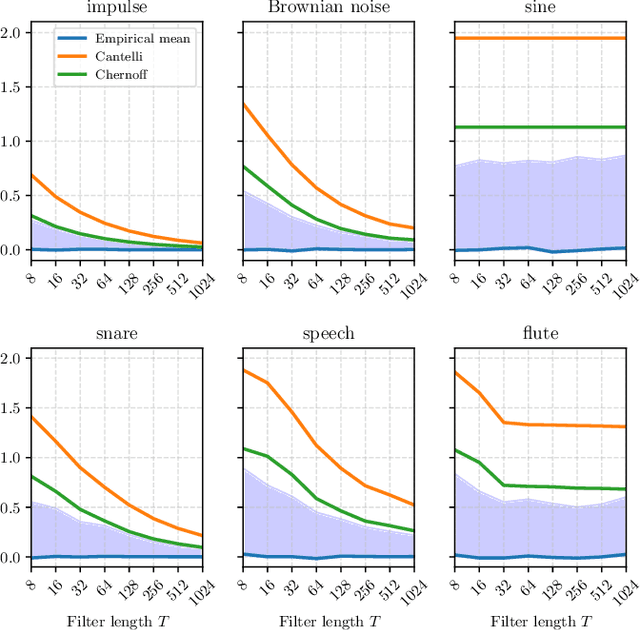
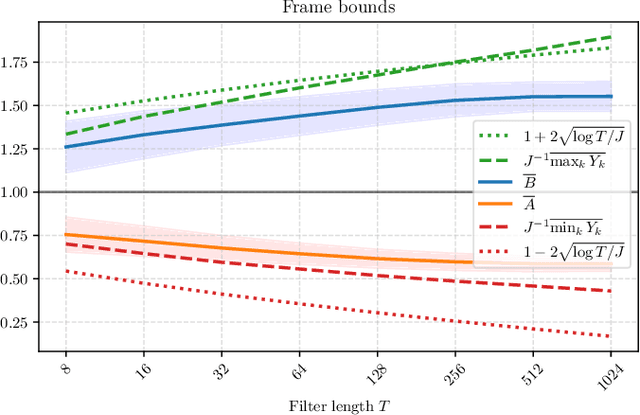
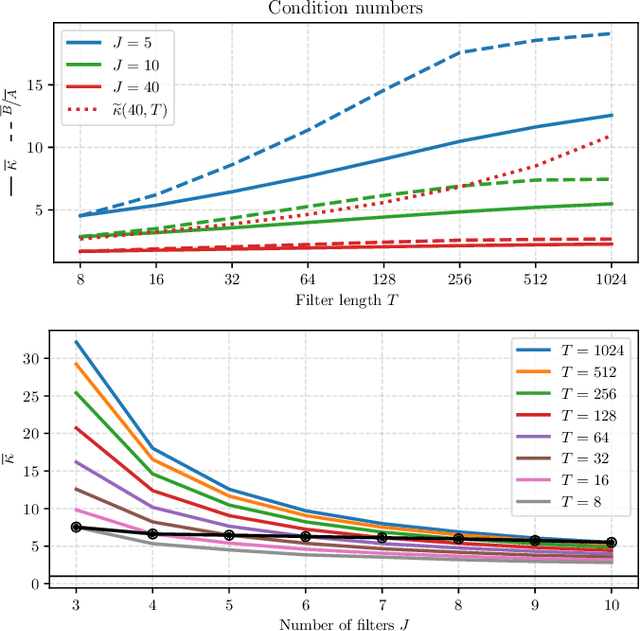
What makes waveform-based deep learning so hard? Despite numerous attempts at training convolutional neural networks (convnets) for filterbank design, they often fail to outperform hand-crafted baselines. This is all the more surprising because these baselines are linear time-invariant systems: as such, their transfer functions could be accurately represented by a convnet with a large receptive field. In this article, we elaborate on the statistical properties of simple convnets from the mathematical perspective of random convolutional operators. We find that FIR filterbanks with random Gaussian weights are ill-conditioned for large filters and locally periodic input signals, which both are typical in audio signal processing applications. Furthermore, we observe that expected energy preservation of a random filterbank is not sufficient for numerical stability and derive theoretical bounds for its expected frame bounds.

Fitting Auditory Filterbanks with Multiresolution Neural Networks

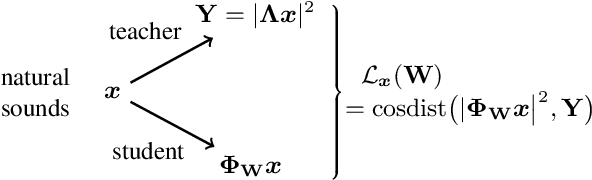
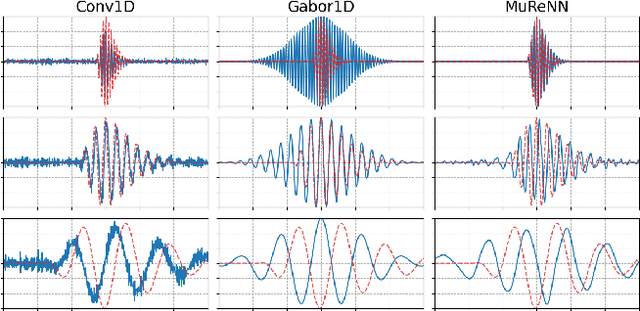
Waveform-based deep learning faces a dilemma between nonparametric and parametric approaches. On one hand, convolutional neural networks (convnets) may approximate any linear time-invariant system; yet, in practice, their frequency responses become more irregular as their receptive fields grow. On the other hand, a parametric model such as LEAF is guaranteed to yield Gabor filters, hence an optimal time-frequency localization; yet, this strong inductive bias comes at the detriment of representational capacity. In this paper, we aim to overcome this dilemma by introducing a neural audio model, named multiresolution neural network (MuReNN). The key idea behind MuReNN is to train separate convolutional operators over the octave subbands of a discrete wavelet transform (DWT). Since the scale of DWT atoms grows exponentially between octaves, the receptive fields of the subsequent learnable convolutions in MuReNN are dilated accordingly. For a given real-world dataset, we fit the magnitude response of MuReNN to that of a well-established auditory filterbank: Gammatone for speech, CQT for music, and third-octave for urban sounds, respectively. This is a form of knowledge distillation (KD), in which the filterbank ''teacher'' is engineered by domain knowledge while the neural network ''student'' is optimized from data. We compare MuReNN to the state of the art in terms of goodness of fit after KD on a hold-out set and in terms of Heisenberg time-frequency localization. Compared to convnets and Gabor convolutions, we find that MuReNN reaches state-of-the-art performance on all three optimization problems.

Convex Geometry of ReLU-layers, Injectivity on the Ball and Local Reconstruction

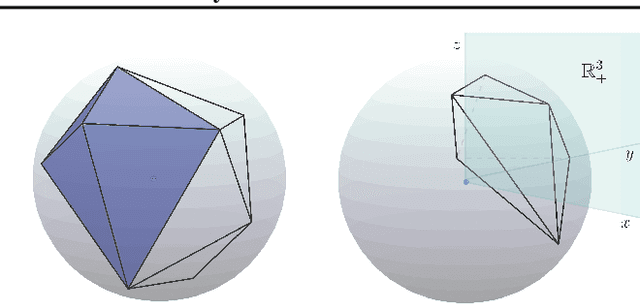
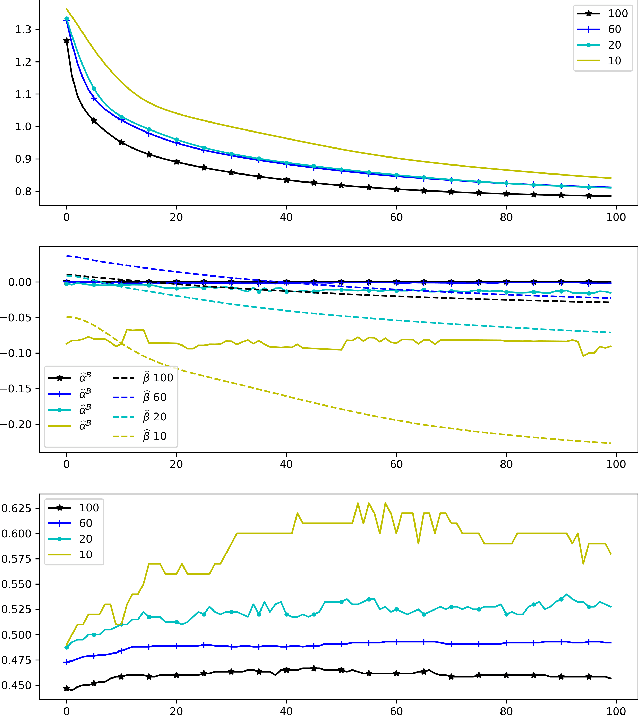
The paper uses a frame-theoretic setting to study the injectivity of a ReLU-layer on the closed ball of $\mathbb{R}^n$ and its non-negative part. In particular, the interplay between the radius of the ball and the bias vector is emphasized. Together with a perspective from convex geometry, this leads to a computationally feasible method of verifying the injectivity of a ReLU-layer under reasonable restrictions in terms of an upper bound of the bias vector. Explicit reconstruction formulas are provided, inspired by the duality concept from frame theory. All this gives rise to the possibility of quantifying the invertibility of a ReLU-layer and a concrete reconstruction algorithm for any input vector on the ball.

Fast Matching Pursuit with Multi-Gabor Dictionaries

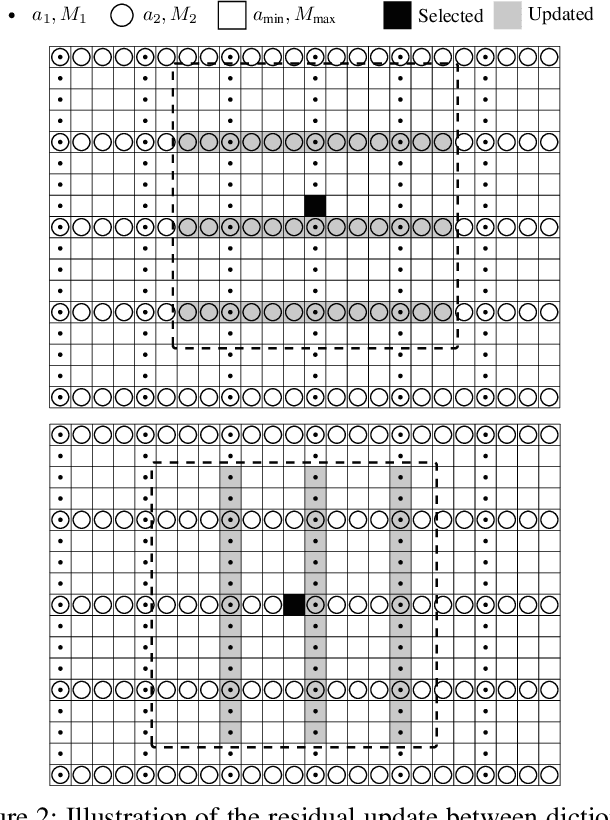
Finding the best K-sparse approximation of a signal in a redundant dictionary is an NP-hard problem. Suboptimal greedy matching pursuit (MP) algorithms are generally used for this task. In this work, we present an acceleration technique and an implementation of the matching pursuit algorithm acting on a multi-Gabor dictionary, i.e., a concatenation of several Gabor-type time-frequency dictionaries, each of which consisting of translations and modulations of a possibly different window and time and frequency shift parameters. The technique is based on pre-computing and thresholding inner products between atoms and on updating the residual directly in the coefficient domain, i.e., without the round-trip to the signal domain. Since the proposed acceleration technique involves an approximate update step, we provide theoretical and experimental results illustrating the convergence of the resulting algorithm. The implementation is written in C (compatible with C99 and C++11) and we also provide Matlab and GNU Octave interfaces. For some settings, the implementation is up to 70 times faster than the standard Matching Pursuit Toolkit (MPTK).

Phase-Based Signal Representations for Scattering

The scattering transform is a non-linear signal representation method based on cascaded wavelet transform magnitudes. In this paper we introduce phase scattering, a novel approach where we use phase derivatives in a scattering procedure. We first revisit phase-related concepts for representing time-frequency information of audio signals, in particular, the partial derivatives of the phase in the time-frequency domain. By putting analytical and numerical results in a new light, we set the basis to extend the phase-based representations to higher orders by means of a scattering transform, which leads to well localized signal representations of large-scale structures. All the ideas are introduced in a general way and then applied using the STFT.

Audio Inpainting via $\ell_1$-Minimization and Dictionary Learning

Audio inpainting refers to signal processing techniques that aim at restoring missing or corrupted consecutive samples in audio signals. Prior works have shown that $\ell_1$- minimization with appropriate weighting is capable of solving audio inpainting problems, both for the analysis and the synthesis models. These models assume that audio signals are sparse with respect to some redundant dictionary and exploit that sparsity for inpainting purposes. Remaining within the sparsity framework, we utilize dictionary learning to further increase the sparsity and combine it with weighted $\ell_1$-minimization adapted for audio inpainting to compensate for the loss of energy within the gap after restoration. Our experiments demonstrate that our approach is superior in terms of signal-to-distortion ratio (SDR) and objective difference grade (ODG) compared with its original counterpart.